插入(二叉搜索树性质是左子树全小,右子树全大):
BinTree Insert(BinTree BST, ElementType X) { BinTree p = BST; if (!p) { BST = (BinTree)malloc(sizeof(struct TNode)); BST->Data = X; BST->Left = BST->Right = NULL; return BST; } BinTree temp; int k; while (p) { temp = p; if (X > p->Data) { p = p->Right; k = 0; } else { p = p->Left; k = 1; } } p = (BinTree)malloc(sizeof(struct TNode)); p->Data = X; p->Left = p->Right = NULL; if (k) temp->Left = p; else temp->Right = p; return BST; }
注意这里要记录结点存放的位置(是父结点的左孩子还是右孩子)。
查找:
Position Find(BinTree BST, ElementType X) { BinTree p = BST; while (p) { if (p->Data == X) { return p; } else if (X > p->Data) { p = p->Right; } else { p = p->Left; } } return NULL; }
查找最小/大的结点(一定在二叉搜索树的最左/右叶子结点):
Position FindMin(BinTree BST) { BinTree p = BST; if (!p) return p; BinTree temp; while (p) { temp = p; p = p->Left; } return temp; } Position FindMax(BinTree BST) { BinTree p = BST; if (!p) return p; BinTree temp; while (p) { temp = p; p = p->Right; } return temp; }
删除:
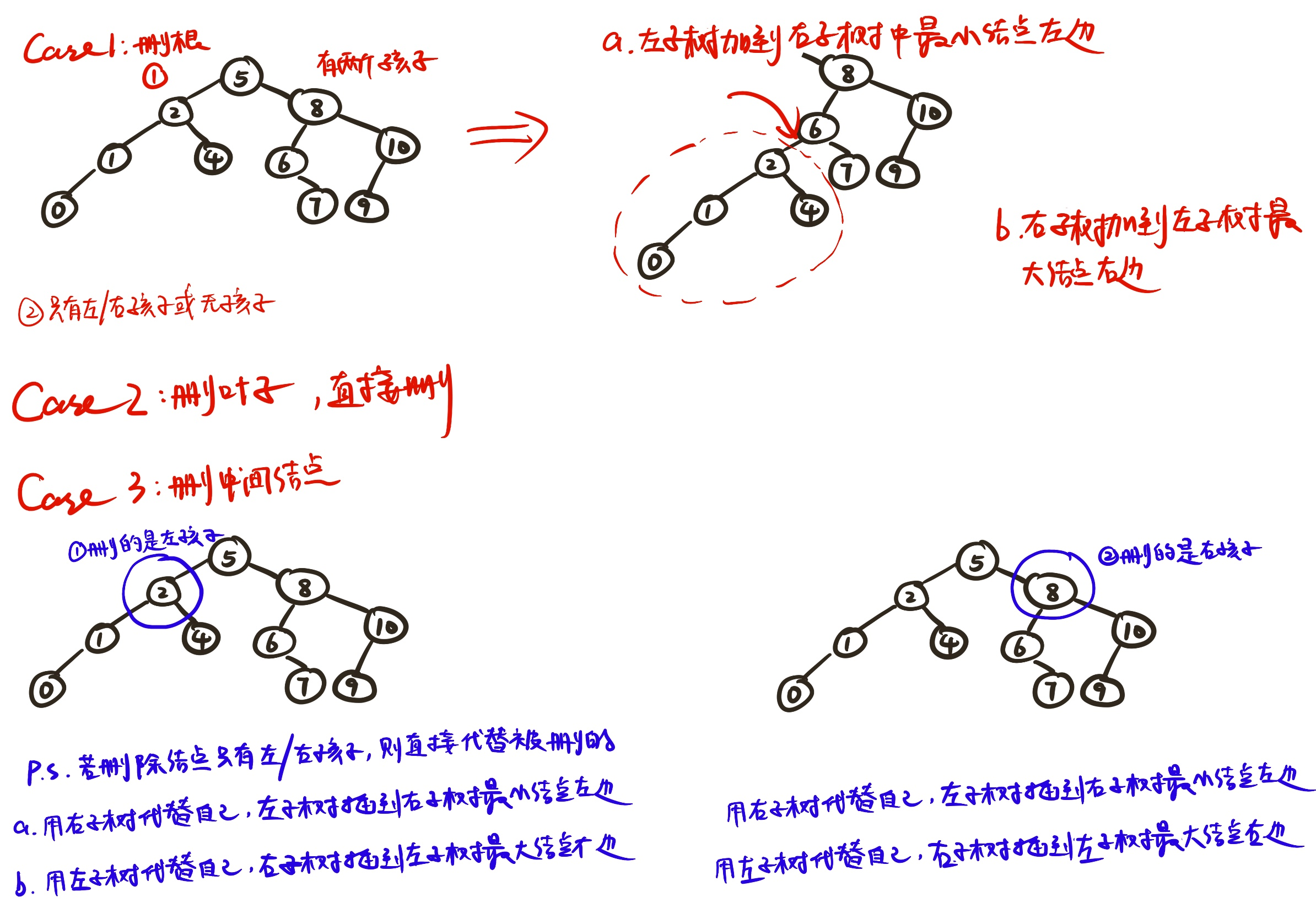
BinTree Delete(BinTree BST, ElementType X) { if (!BST) { printf("Not Found "); return BST; } BinTree insert; BinTree temp; if (X == BST->Data) { if (BST->Left && BST->Right) { temp = BST->Left; BST = BST->Right; insert = FindMin(BST); if(insert) insert->Left = temp; return BST; } if (BST->Left) return BST->Left; else return BST->Right; } BinTree p = BST; temp = p; int k; if (X > p->Data) { p = p->Right; k = 0; } else { p = p->Left; k = 1; } while (p) { if (p->Data == X) { if (k) { if (p->Left && p->Right) { temp->Left = p->Left; insert = FindMax(p->Left); insert->Right = p->Right; } else if (p->Left) temp->Left = p->Left; else if (p->Right) temp->Left = p->Right; else temp->Left = NULL; } else { if (p->Left && p->Right) { temp->Right = p->Right; insert = FindMin(p->Right); insert->Left = p->Left; } else if (p->Left) temp->Right = p->Left; else if (p->Right) temp->Right = p->Right; else temp->Right = NULL; } return BST; } else if (X > p->Data) { p = p->Right; if (k) temp = temp->Left; else temp = temp->Right; k = 0; } else { p = p->Left; if (k) temp = temp->Left; else temp = temp->Right; k = 1; } } printf("Not Found "); return BST; }