一. 简介
1. 什么是栈?
栈是一种只能从表的一端存取数据且遵循 "先进后出"("后进先出") 原则的线性存储结构。栈也是用来存储逻辑关系为 "一对一" 数据的线性存储结构。
C#中提供顺序栈:Stack,它不是线程安全的;如果要使用线程安全的队列,需要用:ConcurrentStack。
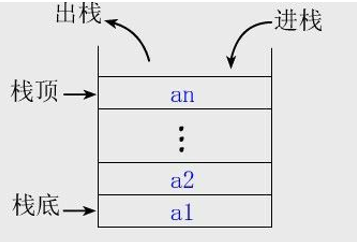
分析:
(1). 栈只能从表的一端存取数据,另一端是封闭的
(2). 在栈中,无论是存数据还是取数据,都必须遵循"先进后出"的原则,即最先进栈的元素最后出栈
2. 一些名词
栈顶(Top):表尾,栈中允许数据插入和删除的那一端。
栈底(Bottom):表头,栈中无法进行数据操作的那一端。
栈上溢(Full):栈内空间已满时,仍进行入栈操作,是一种空间不足的出错状态。
栈下溢(Empty):栈内无数据时,仍然进行出栈操作,是一种数据不足的出错状态。
进栈或者入栈(Push):将数据插入栈顶部。
弹出或出栈(Pop):取出并删除栈顶部的数据。

3. 常用Api
Push()入栈(添加数据)
Pop()出栈(删除数据,返回被删除的数据)
Peek()取得栈顶的数据,不删除
Clear()清空所有数据
Count取得栈中数据的个数
代码分享:

{ Console.WriteLine("--------------C#提供的Stack---------------------"); Stack<int> s1 = new Stack<int>(); s1.Push(1); s1.Push(2); s1.Push(3); s1.Push(4); Console.WriteLine($"元素的个数为:{s1.Count}"); int p1 = s1.Pop(); //取出并删除 Console.WriteLine($"元素的个数为:{s1.Count},取出的数据为:{p1}"); int p2 = s1.Peek(); //取出不删除 Console.WriteLine($"元素的个数为:{s1.Count},取出的数据为:{p2}"); s1.Clear(); Console.WriteLine($"元素的个数为:{s1.Count}"); }
运行结果:

4. 分类
栈是一种 "特殊" 的线性存储结构,因此栈的具体实现有以下两种方式:
(1). 顺序栈:采用顺序存储结构可以模拟栈存储数据的特点,从而实现栈存储结构;
(2). 链栈:采用链式存储结构实现栈结构;
PS: 两种实现方式的区别,仅限于数据元素在实际物理空间上存放的相对位置,顺序栈底层采用的是数组,链栈底层采用的是链表。
二. 顺序栈
1. 思路
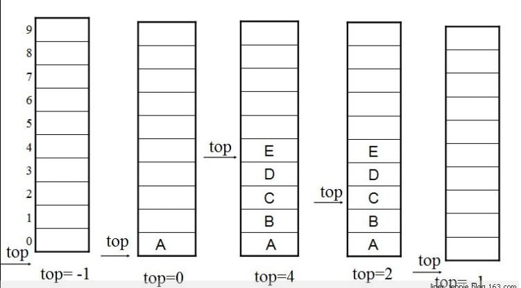
顺序栈,即栈的顺序存储结构(数组),是利用一组地址连续的存储单元依次存放自栈底到栈顶的数据元素,同时附设指针top指示栈顶元素在顺序栈中的位置。
当top=-1时候,表示为空栈。由于顺序栈的操作位置基本在栈顶,所以,不需要查找插入和删除的位置,也不需要移动元素,因而顺序栈的基本操作要比顺序表简单的多,其基本操作时间复杂度均为O(1)。
2. 手撸代码
接口
/// <summary> /// 栈接口 /// </summary> /// <typeparam name="T"></typeparam> public interface IStack<T> { int Count { get; }//元素个数 bool IsEmpty(); //是否为空栈 void Clear(); //清空 void Push(T item); //入栈操作 T Pop(); //返回栈顶数据并且出栈 T Peek(); //取栈顶元素,不出栈 }
实现类

/// <summary> /// 顺序栈 /// (用数组来实现) /// </summary> /// <typeparam name="T"></typeparam> public class SeqStack<T> : IStack<T> { private T[] _array; //底层数据用数组来存储 private const int _defaultCapacity = 4; //默认存储容量 private int top = -1; //指向栈顶元素的位置 top=-1,表示为空元素 /// <summary> /// 指定容量的构造函数 /// </summary> /// <param name="capacity"></param> public SeqStack(int capacity) { if (capacity < 0) { throw new ArgumentOutOfRangeException("栈容量不能小于0"); } //指定容量小于默认容量,则采用默认容量 if (capacity < _defaultCapacity) { capacity = _defaultCapacity; } this._array = new T[capacity]; } /// <summary> /// 无参构造函数 /// (初始化为默认容量) /// </summary> public SeqStack() : this(_defaultCapacity) { } /// <summary> /// 元素个数 /// </summary> public int Count { get { return top + 1; } } /// <summary> /// 清空所有元素 /// </summary> public void Clear() { top = -1; } /// <summary> /// 判断栈是否为空 /// </summary> /// <returns></returns> public bool IsEmpty() { return top == -1; } /// <summary> /// 获取栈顶元素(不删除) /// </summary> /// <returns></returns> public T Peek() { if (IsEmpty()) { throw new InvalidOperationException("栈下溢,栈中没有数据"); } return this._array[top]; } /// <summary> /// 出栈(删除) /// </summary> /// <returns></returns> public T Pop() { T data = Peek(); top--; return data; } /// <summary> /// 入栈 /// </summary> /// <param name="item"></param> public void Push(T item) { //当元素个数等于数组长度,则需要扩容2倍 if (this.Count == this._array.Length) { T[] desArray = new T[this._array.Length * 2]; //原数组copy到目标数组中 Array.Copy(this._array, 0, desArray, 0, this.Count); this._array = desArray; } this._array[++top] = item; } }
调用代码
{ Console.WriteLine("--------------手撸顺序栈---------------------"); IStack<int> s1 = new SeqStack<int>(); s1.Push(1); s1.Push(2); s1.Push(3); s1.Push(4); Console.WriteLine($"元素的个数为:{s1.Count}"); int p1 = s1.Pop(); //取出并删除 Console.WriteLine($"元素的个数为:{s1.Count},取出的数据为:{p1}"); int p2 = s1.Peek(); //取出不删除 Console.WriteLine($"元素的个数为:{s1.Count},取出的数据为:{p2}"); s1.Clear(); Console.WriteLine($"元素的个数为:{s1.Count}"); }
运行结果:

三. 链栈
1. 思路
链栈通常用单链表来表示,它的实现是单链表的简化。由于链栈的操作只是在一端进行,为了操作方便,把栈顶设在链表的头部。单链表获取长度需要遍历整个链表,性能很低,所以我们增加一个count属性记录元素个数。

2. 手撸代码
接口

/// <summary> /// 栈接口 /// </summary> /// <typeparam name="T"></typeparam> public interface IStack<T> { int Count { get; }//元素个数 bool IsEmpty(); //是否为空栈 void Clear(); //清空 void Push(T item); //入栈操作 T Pop(); //返回栈顶数据并且出栈 T Peek(); //取栈顶元素,不出栈 }
实现类

/// <summary> /// 链栈 /// </summary> public class LinkedStack<T> : IStack<T> { public StackNode<T> top; //栈顶指针 public int count = 0; //元素个数 public int Count { get { return count; } } /// <summary> /// 清空元素 /// </summary> public void Clear() { count = 0; top = null; } /// <summary> /// 是否为空 /// </summary> /// <returns></returns> public bool IsEmpty() { return count == 0; } /// <summary> /// 出栈(不删除) /// </summary> /// <returns></returns> public T Peek() { if (top==null) { throw new ArgumentOutOfRangeException("栈下溢,栈内没有数据"); } return top.data; } /// <summary> /// 出栈(删除) /// </summary> /// <returns></returns> public T Pop() { if (top==null) { throw new ArgumentOutOfRangeException("栈下溢,栈内没有数据"); } T r = top.data; top = top.next; count--; return r; } /// <summary> /// 入栈 /// </summary> /// <param name="item"></param> public void Push(T item) { StackNode<T> newNode = new StackNode<T>(item); newNode.next = top; top = newNode; count++; } }
测试
{ Console.WriteLine("--------------手撸链栈---------------------"); IStack<int> s1 = new LinkedStack<int>(); s1.Push(1); s1.Push(2); s1.Push(3); s1.Push(4); Console.WriteLine($"元素的个数为:{s1.Count}"); int p1 = s1.Pop(); //取出并删除 Console.WriteLine($"元素的个数为:{s1.Count},取出的数据为:{p1}"); int p2 = s1.Peek(); //取出不删除 Console.WriteLine($"元素的个数为:{s1.Count},取出的数据为:{p2}"); s1.Clear(); Console.WriteLine($"元素的个数为:{s1.Count}"); }
运行结果

四. 应用
1. 进制转换器
(1).目标:将一个非负的十进制整数N转换成其他D进制数.
(2).原理:
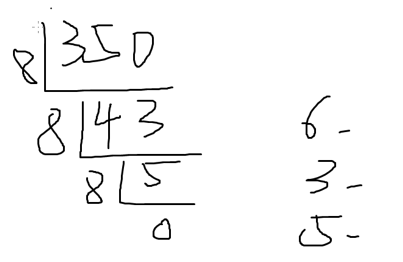
求余→转换成char→入栈→整除→继续循环,最初出栈
特别注意:int→char: char c = residue < 10 ? (char)(residue + 48) : (char)(residue + 55);
代码分享:
public class Utils { /// <summary> /// 十进制N转换成D进制 /// </summary> /// <param name="N"></param> /// <param name="D"></param> /// <returns></returns> public static string DecConvert(int N, int D) { if (D < 2 || D > 16) { throw new ArgumentOutOfRangeException("D", "只支持二进制到十六进制的转换"); } Stack<char> stack = new Stack<char>(); do { int residue = N % D; //取余 char c = residue < 10 ? (char)(residue + 48) : (char)(residue + 55); stack.Push(c); //进栈 N = N / D; } while (N != 0); //当除的结果为0时表示已经到最后一位了 string s = string.Empty; while (stack.Count > 0) { //所有的元素出栈并压入字符串s内 s += stack.Pop().ToString(); } return s; } }
测试:
{ Console.WriteLine("--------------进制转换---------------------"); //十进制的365转换成八进制输出 string result1 = Utils.DecConvert(350, 8); Console.WriteLine($"十进制的365转换成八进制输出:{result1}"); }
运行结果:

2. 其它案例
(1). 高性能分页

(2). 浏览器回退功能
我们经常使用浏览器在各种网站上查找信息。假设先浏览的页面 A,然后关闭了页面 A 跳转到页面 B,随后又关闭页面 B 跳转到了页面 C。而此时,我们如果想重新回到页面 A,有两个选择:
- 重新搜索找到页面 A;
- 使用浏览器的"回退"功能。浏览器会先回退到页面 B,而后再回退到页面 A。
浏览器 "回退" 功能的实现,底层使用的就是栈存储结构。当你关闭页面 A 时,浏览器会将页面 A 入栈;同样,当你关闭页面 B 时,浏览器也会将 B入栈。因此,当你执行回退操作时,才会首先看到的是页面 B,然后是页面 A,这是栈中数据依次出栈的效果。
(3). 括号匹配问题
数编程语言都会用到括号(小括号、中括号和大括号),括号的错误使用(通常是丢右括号)会导致程序编译错误,而很多开发工具中都有检测代码是否有编辑错误的功能,其中就包含检测代码中的括号匹配问题,此功能的底层实现使用的就是栈结构。
思路:
A. 如果碰到的是左圆括号或者左大括号,直接入栈;
B. 如果碰到的是右圆括号或者右大括号,就直接和栈顶元素配对:如果匹配,栈顶元素出栈;反之,括号不匹配;
!
- 作 者 : Yaopengfei(姚鹏飞)
- 博客地址 : http://www.cnblogs.com/yaopengfei/
- 声 明1 : 如有错误,欢迎讨论,请勿谩骂^_^。
- 声 明2 : 原创博客请在转载时保留原文链接或在文章开头加上本人博客地址,否则保留追究法律责任的权利。
