比较均值:列表和图形
拆分文件
单因素方差分析
双因素方差分析(含交互项、只含主效应)
组间两两比较
随机因素分析
方差分析原理:
变异分解。将样本的总变异分解为随机误差的作用、某影响因素的作用。通过比较某影响因素所致变异与随机误差所致变异的大小建立F检验统计量进行检验。
yij=总平均+ai+随机误差项
检验ai是否为0。
1、案例背景
分析10种不同口味(8个竞争品牌、2各试制品)酸奶有无差异,以及城市因素是否对其有影响。
2、数据理解
用交叉表(数据-描述统计-交叉表)看原始数据结构。
均值的列表描述:

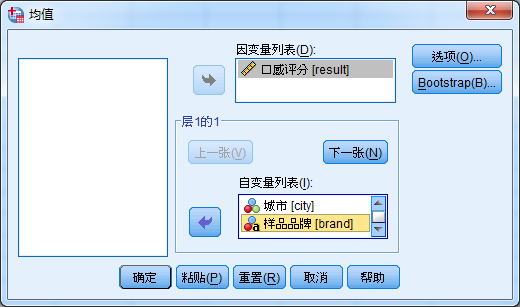
均值的图形描述:
此例画的是误差条形图。

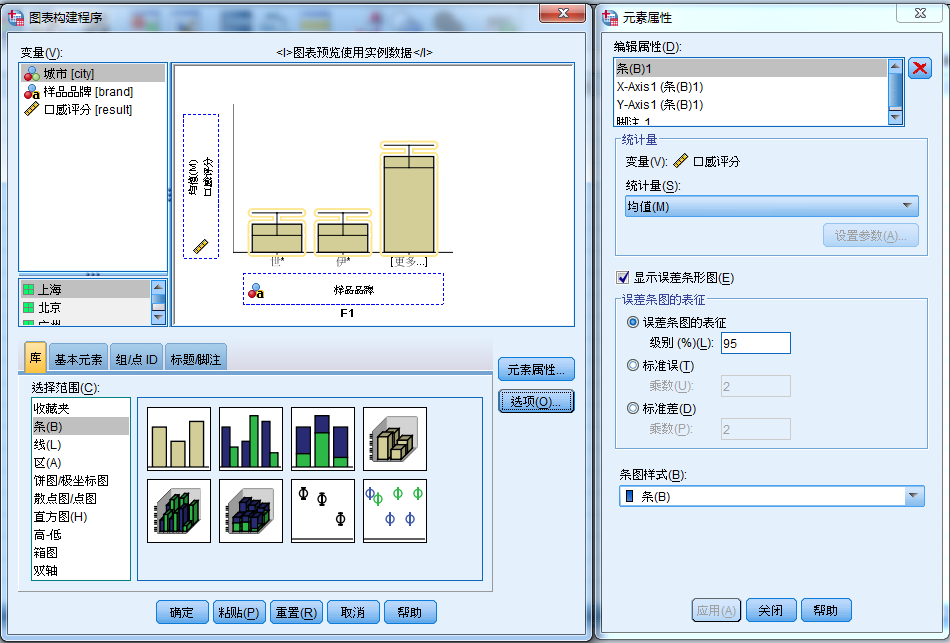
3、不同品牌的评分差异分析
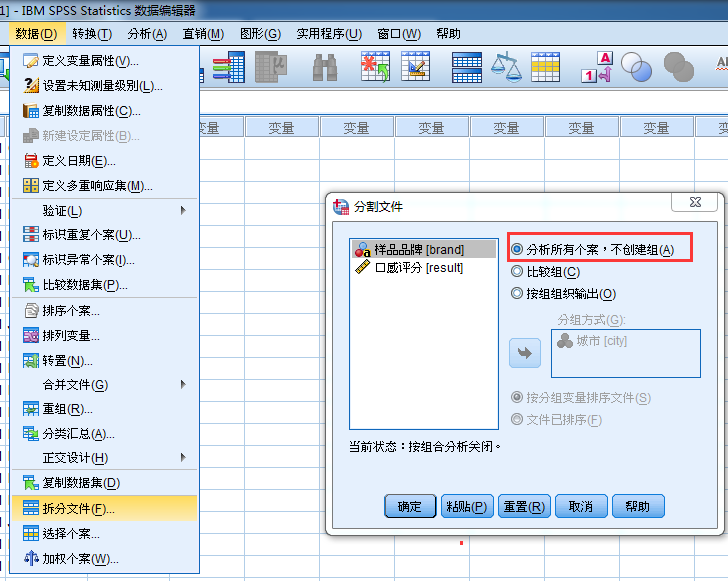
先剔除城市因素的影响,所以要先进行拆分文件。


方差分析模型的假设条件:独立性、正态性、方差齐性。
方差分析的模型检验包括总模型检验(原假设:模型中涉及的所有因素的实际影响均为0)、各因素检验(原假设:每个因素的实际影响为0)
品牌作用的总体检验:
单因素方差分析有两种:一是“分析-比较均值-单因素ANOVA”,一是“如下”。

结论:在同一城市,酸奶不同品牌间存在差异。
问题:那哪些品牌间存在差异呢?需要进行两两比较。
组间两两比较:

结论:不同亚组间的P值小于0.05,即亚组间有差异;同一亚组内P值大于0.05,两两无差异。
方差齐性检验:

实际上,方差分析模型对假设条件有一定的忍耐性。对于独立性,一般从研究设计或数据背景就可以大致评估;对于正态性,只要不是严重的偏态,在样本量较大的时候结果很稳定;对于方差齐性,只要所有组中的最大方差、最小方差之比小于3,则检验结果也很稳定。
4、两因素方差分析模型
拟合包含交互项的饱和模型:
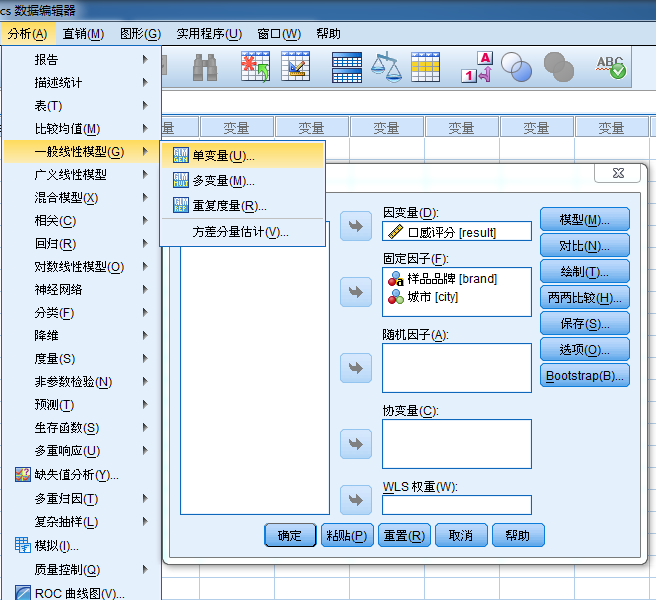
拟合只包含主效应的模型:(交互项不显著,所以去掉交互项)

组间两两比较(品牌间、城市间的口感评分有差异,要分析哪个城市、哪个品牌有差异)

随机因素分析:
固定因素:该因素在样本中所有可能的水平都出现了。
随机因素:该因素所有可能的取值在样本中并没有全部出现,或不可能全部出现。此时将该因素已出现的水平泛化到适合所有可能出现的水平。
判断一个因素是固定还是随机,是根据研究目的而定。
研究10种不同口味酸奶在4个城市间是否存在差异。固定因素:酸奶品种、城市。
研究10中不同口味酸奶在全国城市间是否存在差异。固定因素:酸奶品种。随机因素:4个城市。(由4个城市外推至全国)
