概率论与数理统计-ch4-随机变量的数字特征

分布函数能完整的描述随机变量的统计特征，但很多时候没有必要，只需知道随机变量的某些重要特征。所以引入数学期望即均值、方差等概念。

1、数学期望

指试验中每次可能结果的概率乘以其结果的总和，反映随机变量平均取值的大小。

离散型：

连续型：

设连续性随机变量X的概率密度函数为f(x)，若积分绝对收敛，则称积分的值为随机变量的数学期望，记为E(X)。

定理：

设Y是随机变量X的函数：Y=g（X）（g（X）是连续函数），

当X时离散型，它的分布律为  若 绝对收敛，则有:

当X时连续型，它的概率密度为f(x)，若  绝对收敛，则有:

该定理的意义在于：我们求E（Y）时不需要算出Y的分布律或者概率密度，只要利用X的分布律或概率密度即可。

上述定理还可以推广到两个或以上随机变量的函数情况。

 

设C为一个常数，X和Y是两个随机变量。以下是数学期望的重要性质：

1.E（C）=C

2.E（CX）=CE（X）

3.E(X+Y)=E(X)+E(Y)

4.当X和Y相互独立时，E(XY)=E(X)E(Y)

 

2、方差

研究随机变量与其均值的偏离程度，引入方差。方差刻画了随机变量X取值的分散程度。

设X是一个随机变量，若  存在，则称  为X的方差，记为D(X),Var(X)或DX。

标准化变量：

不管随机变量X服数学期望从什么分布，只要具有E(X)=µ，方差D(X)=σ² ，则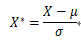的数学期望为0，方差为1。称X^* 为X的标准化变量。

方差的性质：

切比雪夫不等式：

设随机变量X的数学期望和方差都存在，则对任意常数 ε>0，有P( | X - E(X) | ≥ ε ) ≤ D(X) / ε² ，或P( | X - E(X) | < ε ) ≥ 1 - D(X) / ε²

切比雪夫不等式说明，DX越小，则 P{|X-EX|>=ε} 越小，P{|X-EX|<ε}越大， 也就是说，随机变量X取值基本上集中在EX附近，这进一步说明了方差的意义。

3、协方差及相关系数

协方差用于衡量两个变量总体误差的期望。

期望值分别为E[X]与E[Y]的两个实随机变量X与Y之间的协方差Cov(X,Y)定义为：

 如果两个变量的变化趋势一致，也就是说如果其中一个大于自身的期望值时另外一个也大于自身的期望值，那么两个变量之间的协方差就是正值；如果两个变量的变化趋势相反，即其中一个变量大于自身的期望值时另外一个却小于自身的期望值，那么两个变量之间的协方差就是负值。

协方差的性质：

（1）Cov(X，Y)=Cov(Y，X)；

（2）Cov(aX，bY)=abCov(X，Y)，（a，b是常数）；

（3）Cov(X1+X2，Y)=Cov(X1，Y)+Cov(X2，Y)。

由协方差定义，可以看出Cov(X，X)=D(X)，Cov(Y，Y)=D(Y)。

 

为了消除量纲的影响：

定义

  称为随机变量X和Y的(Pearson)相关系数。

定理：

设ρXY是随机变量X和Y的相关系数，则有

（1）∣ρXY∣≤1；

（2）∣ρXY∣=1充分必要条件为P{Y=aX+b}=1，（a，b为常数，a≠0）

 

ρXY是一个表征X,Y之间线性关系紧密程度的量。

 

ρXY=0，则X和Y线性不相关。但得不出X和Y独立的结论。

 X和Y独立，则ρXY=0

对于二维正态随机变量(X,Y)， X和Y不相关等价于 X和Y独立。条件都是ρXY=0。

 

4、矩、协方差矩阵

设X和Y是随机变量，若E(X^k)，k=1，2，...存在，则称它为X的k阶原点矩，简称k阶矩。

若E{[X-E(X)]k}，k=1，2，...存在，则称它为X的k阶中心矩。

若E(X^kY^p)，k、l=1，2，...存在，则称它为X和Y的k+p阶混合原点矩。

若E{[X-E(X)]^k[Y-E(Y)]^l }，k、l=1，2，...存在，则称它为X和Y的k+l阶混合中心矩。

显然，X的数学期望E(X)是X的一阶原点矩，方差D(X)是X的二阶中心矩，协方差Cov(X，Y)是X和Y的二阶混合中心矩。

 协方差矩阵

协方差矩阵的每个元素是各个向量元素之间的协方差。是从标量随机变量到高维度随机向量的自然推广。

协方差矩阵被定义为：

Σ=E  

 

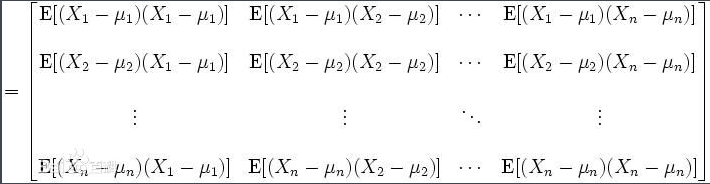
（即：一个n阶行向量，乘以一个n阶列向量，得到一个n*n的矩阵）

 n维正态变量具有四个重要性质。略