概率论与数理统计-ch3-多维随机变量及其分布

1、二维随机变量

当描述一个随机试验时需要用到两个或两个以上随机变量时，如：一个学生的身高和体重，一个炮弹落地点位置的横坐标和纵坐标。这时就用到了二维或多维随机变量。

二维随机变量( X,Y)的性质不仅与X 、Y 有关,而且还依赖于这两个随机变量的相互关系。因此，逐个地来研究X或Y的性质是不够的，还需将（X，Y）作为一个整体来研究。

二维随机变量分布函数的几何意义：

将二维随机变量（X，Y）看成是平面上随机点的坐标，分布函数F（x，y）在（x，y）处的函数值就是随机点（X，Y）落在以（x，y）为顶点而位于该点左下方的无穷矩形区域内的概率。

基本性质同一维随机变量分布函数。

二维离散型随机变量的分布律：

P{X=x_i,Y=y_j}=p_ij

二维离散型随机变量的分布函数：

二维随机变量(X,Y)的概率密度：

分布函数F(x,y)描述的是曲面z=f(x,y)与平面xOy的[-∞,x]*[-∞,y]面积组成的曲面柱体的体积。

2、边缘分布

边缘分布函数

边缘分布律

边缘概率密度

 

注：二维随机变量（X，Y）的分布函数F(x,y)可以确定边缘分布FX（x），FY（y），但后两者不能确定前者。

3、条件分布

条件分布律

设（X，Y)是二维离散型随机变量，对于固定的j，若P{Y=yj}>0，则称

为在Y=yj条件下随机变量X的条件分布律。

条件分布函数

称为在Y=y条件下的X的条件分布函数。

条件概率密度

称为在Y=y条件下的X的条件概率密度。

 4、相互独立的随机变量

5、两个随机变量的函数的分布

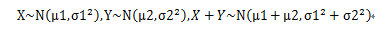
经过证明得出结论：有限个相互独立的正态随机变量的线性组合仍然服从正态分布。