四叉树搜索附近的人

现在很多的APP都有"附近的人"功能。

粗略的思考一下，用户在登录的时候会将自己的位置信息告诉服务器，服务器会记录一份用户的位置信息列表。

假设服务器里只有10个人，那么要找附近的人就很简单，只需写一个算距离的函数，然后依次遍历长度是10的位置信息列表，距离从近到远排序，返回排序后的列表即可。

那么如果服务器里有1千万人呢，或者几亿人呢，比如微信。这时再从头到尾遍历（复杂度O(n)）就不适合了。

通常情况下会使用“四叉树”来构建这些大量的位置信息。

1.四叉树

顾名思义，四叉树是叶子节点最多为4的树结构。由于采用的树结构，复杂度则变成了树的深度 O(logn)了。

2.地理位置和四叉树

把全球的位置定义为一个矩形，用经度和纬度的二维数据来定位全球范围内的点。

纬度范围[-90,90]，经度范围[-180,180]。

当登录服务器的人数越来越多时，超过一个约定的值，就将这个矩形分割成4个更小的矩形，将这些位置信息分发到更小的矩形里（比如分成太平洋，大西洋等）

更小的矩形存储的信息又要超过约定的值了，就再分割。

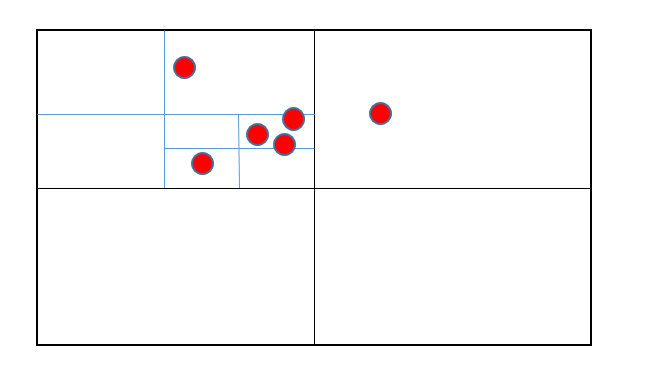
3.查找附近的点

假设我在广州天河的华农的图书馆，想要找到附近的10个人的位置。

那么首先需要从根节点（全球）遍历到天河区的节点，搜寻这个节点的列表里有没有10个人。

如果不够10个人，则向上一层的广州节点请求，可能会在海珠区找到剩余的人。

4.C++描述算法

以上就是四叉树搜索位置的关键点，那么就简单用C++来编写代码描述这个算法。

github：https://github.com/yao2yao/QuadTree.git

我采用的是位置全部信息存储在叶子的四叉树。

首先是核心的数据结构树的节点：

struct QuadTreeNode
    {
        QuadTreeNode(){}
        Rect        rect;                    //节点代表的矩形区域
        std::vector<PosInfo> pos_array;        //节点中的位置信息
        int            child_num;                //节点的孩子节点数量
        QuadTreeNode *child[CHILD_NUM];        //指向孩子节点的指针
        int            depth;                    //节点的深度
    };

创建一个节点：

void QuadTree::CreateQuadTreeNode(int depth, Rect rect, QuadTreeNode *p_node)
{
    p_node->depth = depth;
    p_node->child_num = 0;
    p_node->pos_array.clear();
    p_node->rect = rect;
    for (int i = 0; i < CHILD_NUM; ++i)  
    {  
        p_node->child[i] = NULL; 
    }
}

分割一个节点：

这里采用均分法，即取x坐标和y坐标的一半划分。new四个节点，并且作为当前结点的4个孩子节点。

void QuadTree::Split(QuadTreeNode *pNode)
{
    int start_x = pNode->rect.lb_x;
    int start_y = pNode->rect.lb_y;
    int sub_width = (pNode->rect.rt_x - pNode->rect.lb_x) / 2;
    int sub_height = (pNode->rect.rt_y - pNode->rect.lb_y) / 2;
    int end_x = pNode->rect.rt_x;
    int end_y = pNode->rect.rt_y;

    QuadTreeNode *p_node0 = new QuadTreeNode;
    QuadTreeNode *p_node1 = new QuadTreeNode;
    QuadTreeNode *p_node2 = new QuadTreeNode;
    QuadTreeNode *p_node3 = new QuadTreeNode;

    CreateQuadTreeNode(pNode->depth + 1, Rect(start_x + sub_width, start_y + sub_height, end_x, end_y), p_node0);
    CreateQuadTreeNode(pNode->depth + 1, Rect(start_x, start_y + sub_height, start_x + sub_width, end_y), p_node1);
    CreateQuadTreeNode(pNode->depth + 1, Rect(start_x, start_y, start_x + sub_width, start_y + sub_height), p_node2);
    CreateQuadTreeNode(pNode->depth + 1, Rect(start_x + sub_width, start_y, end_x, start_y + sub_height), p_node3);

    pNode->child[0] = p_node0;
    pNode->child[1] = p_node1;
    pNode->child[2] = p_node2;
    pNode->child[3] = p_node3;

    pNode->child_num = 4;
}

一个辅助函数，给一个指定节点，和目标位置，返回所在的象限。
象限划分：

/* 一个矩形区域的象限划分：
    
    UL(1)   |    UR(0) 
    --------|----------- 
    LL(2)   |    LR(3) 

*/
        

int QuadTree::GetIndex(PosInfo pos, QuadTreeNode *pNode)
{
    int start_x = pNode->rect.lb_x;
    int start_y = pNode->rect.lb_y;
    int sub_width = (pNode->rect.rt_x - pNode->rect.lb_x) / 2;
    int sub_height = (pNode->rect.rt_y - pNode->rect.lb_y) / 2;
    int end_x = pNode->rect.rt_x;
    int end_y = pNode->rect.rt_y;
    
    start_x + sub_width, start_y + sub_height, end_x, end_y;
    //0象限
    if ((pos.latitude >= start_x + sub_width) 
    && (pos.latitude <= end_x) 
    && (pos.longitude >= start_y + sub_height) 
    && (pos.longitude <= end_y))
    {
        return UR;
    }
    //1象限
    else if ((pos.latitude >= start_x) 
    && (pos.latitude < start_x + sub_width) 
    && (pos.longitude >= start_y + sub_height) 
    && (pos.longitude <= end_y))
    {
        return UL;
    }
    //2象限
    else if ((pos.latitude >= start_x) 
    && (pos.latitude < start_x + sub_width) 
    && (pos.longitude >= start_y) 
    && (pos.longitude < start_y + sub_height))
    {
        return LL;
    }
    //3象限
    else if ((pos.latitude >= start_x + sub_width) 
    && (pos.latitude <= end_x) 
    && (pos.longitude >= start_y) 
    && (pos.longitude < start_y + sub_height))
    {
        return LR;
    }
    else
    {
        return INVALID;
    }
}

接下来是关键点，插入函数，当数据一组一组出现的时候，如何构建一棵四叉树：

可以从根节点开始，如果该节点有孩子，则插入对应象限的孩子节点。

否则的话，判断当前结点的位置信息容量和深度。

如果位置信息还没满，深度在预先设定的范围内，则将位置信息插入当前结点。

否则需要将当前结点分割，并且把位置信息分发到各个新的孩子节点，删除自身的位置信息。然后重新对当前结点做一次插入操作。

void QuadTree::Insert(PosInfo pos, QuadTreeNode *p_node)
{
    if (p_node == NULL)
    {
        return;
    }

    if (p_node->child_num != 0)
    {
        int index = GetIndex(pos, p_node);
        if (index >= UR && index <= LR)
        {
            Insert(pos, p_node->child[index]);
        }
    }
    else
    {
        if ((int)p_node->pos_array.size() >= m_maxobjects && p_node->depth < m_depth)
        {
            Split(p_node);
            for (std::vector<PosInfo>::iterator it = p_node->pos_array.begin(); it != p_node->pos_array.end(); ++it)
            {
                Insert(*it, p_node);
            }
            p_node->pos_array.clear();
            Insert(pos, p_node);
        }
        else
        {
            p_node->pos_array.push_back(pos);
        }
    }
}

搜索附近的点：

从根节点遍历到目标节点所在节点，遍历该节点所有的位置信息点。

假如数量不够，则向上到父节点，搜寻兄弟节点，直到获得足够数量的位置信息点。

void QuadTree::Search(int num, PosInfo pos_source, std::vector<PosInfo> &pos_list, QuadTreeNode *p_node)
{
    if (p_node == NULL)
    {
        return;
    }

    if ((int)pos_list.size() >= num)
    {
        return;
    }

    if (p_node->child_num == 0)
    {
        for (std::vector<PosInfo>::iterator it = p_node->pos_array.begin(); it != p_node->pos_array.end(); ++it)
        {
            if ((int)pos_list.size() >= num)
            {
                return;
            }
            pos_list.push_back(*it);
        }
        return;
    }

    //目标节点
    int index = GetIndex(pos_source, p_node);
    if (index >= UR && index <= LR)
    {
        if (p_node->child[index] != NULL)
        {
            Search(num, pos_source, pos_list, p_node->child[index]);
        }
    }

    //目标节点的兄弟节点
    for (int i = 0; i < CHILD_NUM; ++i)
    {
        if (index != i && p_node->child[i] != NULL)
        {
            Search(num, pos_source, pos_list, p_node->child[i]);
        }
    }
}

如果算法没错的||—_—||

数据测试，随机1千万组数据，输入一个目标位置，搜索15个附近点的耗时是2毫秒。

随机1亿组数据，耗时是37毫秒。（插入数据用了一个小时，打印了一个1G的TXT）。。。。