首先我们需要搞清楚几个概念:概率函数、概率分布、概率密度
我这里只做简单阐述,意在理解概念,可能不严谨。
我们知道变量可分为离散随机变量和连续随机变量;
概率函数:随机变量取某个值的概率
pi=P(X=ai)(i=1,2,3,4,5,6);以骰子为例,每次摇骰子取值为 1-6,取每个数字的概率为 1/6,这就是离散概率函数;
pi=P(X<170);以身高为例,小于 170 的概率,这就是连续概率函数
描述了取某个值或者某一个区间的概率
概率分布:也叫累积概率函数,随机变量取某些值的概率,也就是取这些值的概率的累加和
pi=P(X=[1, 2])
pi=P(X<170 and X>165)
描述了取某些值或某些区间的概率
概率密度:它只针对连续型随机变量,连续型随机变量的概率函数也叫概率密度
数学上用如下公式表示概率密度
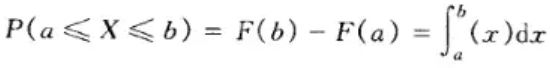
可以看到 X 的取值是连续的,P 是一个积分

F(x) 左图表示连续型随机变量的概率分布;f(x) 右图表示连续型随机变量的概率密度;
f(x) 是 F(x) 的导数
均匀分布
应该说是最简单的分布,它是指在一个取值范围内取到每个值的概率相等;
对于离散型随机变量,概率函数为
P(X)=1/a-b a<b 代表取值范围
对于连续型随机变量,就是可以等概率地取 a b 之间的任一个数
期望:u=(a+b)/2;方差:var=(a-b)2/12
扩展
它适用于连续型变量和离散型变量
场景描述
投骰子
高斯分布
也叫正态分布,是最常见的分布,世界上大部分数据应该是满足高斯分布的,其图形如下
均匀的分布在某点两侧,当然没那么平滑也算高斯,大部分没这么平滑
伯努利分布
也叫两点分布;
稍微官方的概念:在相同条件下重复 n 次试验,如果每次试验只有两个相对立的事件,且各次试验中发生的概率不变,我们成这样的试验为 n 重伯努利试验
通俗解释:只有两个结果的事件;如抛硬币
我们一般把结果即为 {0, 1},如抛硬币 0 是反面,1 是正面;
而且我们通常把 1 发生的概率记为 P(x=1) = p,那么 0 发生的概率则为 P(x=0) = 1-p;
那么 x 的概率可记为 P(x) = px(1-p)1-x (x 取值 0,1 )
说的官方点,x 服从参数为 p 的伯努利分布
期望:E(x) = p;方差:var(x) = p(1-p)
扩展
1. 伯努利分布是离散型分布
2. 逻辑回归二分类就是伯努利分布
场景描述
抛一次硬币
二项分布
接着 伯努利分布 讲,我们做 n 次独立实验得到 结果集 D, 其中正面朝上的事件发生了 x 次,如果 n 为 1,就是伯努利分布,如果 n 大于 1,则为二项分布,其概率函数为
 p 为每次正面朝上的概率
p 为每次正面朝上的概率
期望:E(x) = np;方差:var(x) = np(1-p)
扩展
1. 二项分布也是离散型分布
2. 还以 逻辑回归 为例,如果只有一个模型,结果服从 伯努利分布; 如果进行有放回的抽样,训练 多个模型,则结果服从 二项分布;这里是不是有点像 bagging?
3. 当 p = 1 - p,即 p = 0.5 时,二项分布的直方图(或者概率条形图)是对称的,很容易理解,或者举个例子带入公式也可理解
4. 当 n 趋近于无穷大时,二项分布近似等于正态分布,也就是说,正态分布是二项分布的极限

场景描述
抛 n 次硬币,当我们抛了无穷多次,那不就是正态分布吗
泊松分布
适合描述单位时间(空间)内随机事件发生的次数
比如有 100 个人,其中有 1 个男性的概率?有 2 个男性的概率? 假如我有个先验知识,所有人中男性的占比为 60%,就能计算有 k 个男性的概率
 λ 即为先验概率, k 为发生次数
λ 即为先验概率, k 为发生次数
期望和方差都是 λ
扩展
1. 从定义来看,好像和 二项分布 差不多啊,他们之间确实有关系;
从概念上讲,泊松分布适合实验次数多,且单位时间发生的概率很低的情况,如交通事故;
当 n 很大 p 很小时,二项分布近似等于泊松分布,其中 λ 为 np
从数学上讲,二项分布可以推导出泊松分布

2. 泊松分布可以近似地看成离散变量的高斯分布
场景描述
泊松分布适合于描述单位时间(或空间)内随机事件发生的次数。如某一服务设施在一定时间内到达的人数,电话交换机接到呼叫的次数,汽车站台的候客人数,机器出现的故障数,自然灾害发生的次数,一块产品上的缺陷数,显微镜下单位分区内的细菌分布数等等
指数分布
接着 泊松分布 讲,泊松分布用于单位时间内发生的次数,
但是如果发生了 0 次,也就是没有发生,则泊松分布为 P(X=0)=e-λ;也就是说发生的概率是 P(X!=0)=1 - e-λ,发生而不管发生了多少次;
同时我们也可以把 发生了 x 次记为 发生,那么每次发生的概率 为 xλ,所以我们可以把指数分布扩展为
P(X<x) = e-xλ 没发生
P(X>x) = 1 - e-xλ 发生
期望:u=1/λ;方差:var=1/λ2
扩展
1. 所以指数分布常用于会不会发生
2. 指数分布和泊松分布有一定联系
场景描述
机器是否会故障
参考资料:
https://blog.csdn.net/u014296502/article/details/81069042
https://blog.csdn.net/lin360580306/article/details/51228966
http://www.raincent.com/content-10-10914-1.html
https://blog.csdn.net/weixin_44355973/article/details/98473503
https://baike.baidu.com/item/%E6%B3%8A%E6%9D%BE%E5%88%86%E5%B8%83/1442110?fr=aladdin