SVM,中文名叫支持向量机。
在深度学习出现以前,它是数据挖掘的宠儿;
SVM具有十分完整的数据理论证明,但同时理论也相当复杂。
初识SVM
同其他分类算法一样,SVM分类也是寻找合适的决策边界,为方便理解,以二分类为例。
假设存在二分类样本,我们一定可以找到一个超平面将类别分开,但是通常会存在很多这样的超平面。
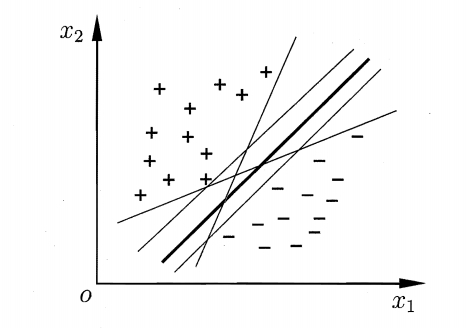
那取哪个呢?
直观感受
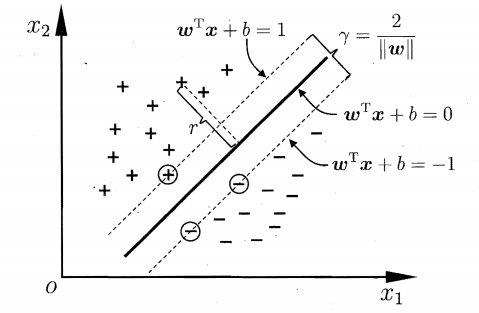
直观来看,应该取中间那条粗线,因为这条线对样本的“容忍性”最好,也就是说样本发生微小变化,不会影响分类结果,但是其他细线,如果样本发生微小变化,都会使得分类结果发生变化,也就是说粗线作为决策边界,其鲁棒性最好。
数学解释
从直观上看,取粗线为宜,但是这条粗线有很多的平行线,都可以实现分类,那么怎么取呢?
我们把这条粗线向两边平移,直至粗线和两边离他最近的样本重合,此时生成了2个新的超平面,记为 b11,b12,然后我们可以把之前的粗线移动到b11和b12的中间,确保粗线到b11和b12的距离相等
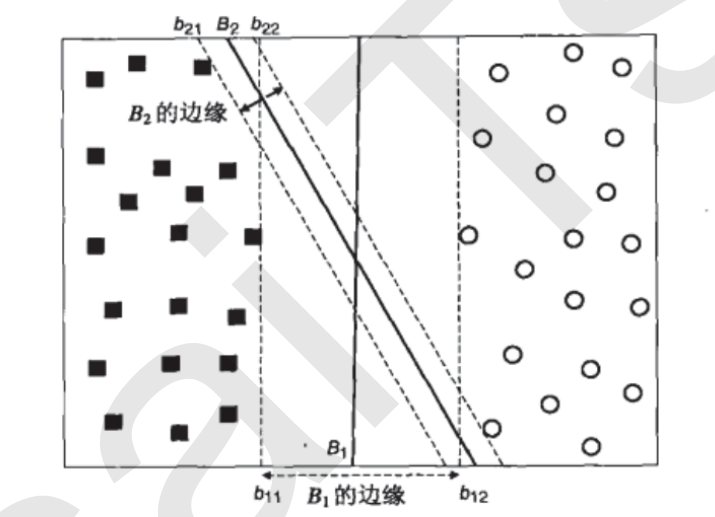
假设我们有两条粗线B1,B2,分别完成上述操作,
b11和b12之间的距离,叫做B1这条决策边界的边际(margin),也有叫“间隔”,记为d,当然也有把b11和B1的距离叫边际的,无所谓,不影响理论
显然拥有更大的边际的决策边界泛化能力更强
与b11和b12相交的样本点叫支持向量
数学建模
如何找到具有最大边际的决策边界呢?
假设这个超平面为 wx+b=0
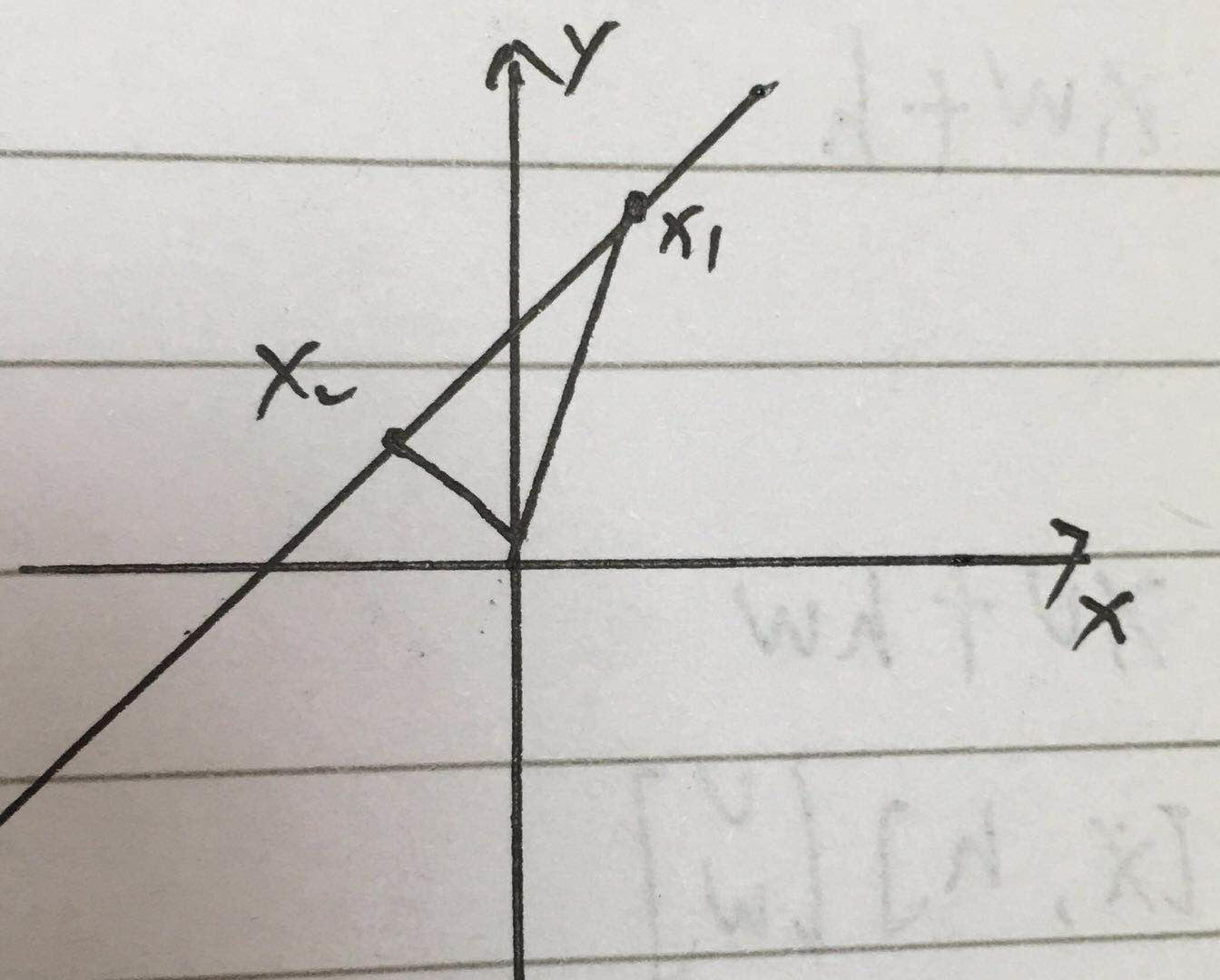
超平面上取两点x1,x2,则
wx1+b=0
wx2+b=0
w(x1-x2)=0,故w与x1-x2垂直,即w为超平面的法向量。
超平面外任意点到平面的距离为

此时把支持向量带入上式,即可得到
d=2r,带有绝对值,不好处理。

解释
1. 上图把超平面的表达形式稍微变化了一下,而且进行了一系列的推导
2. 其实最开始也有解释,如果向两侧平移不同距离,那么应该先调整决策边界到两个新平面的中间,此时3个平面的wb都要做调整。
3. 上图是许多资料未讲明的地方
4. 上图是个变换过程,如果二分类的标签不是-1 1,也可以变换成-1 1
上图的结论是
假设是二分类,那么决策边界 wx+b=0 向两侧平移1,可得

等号成立的条件就是支持向量,此时 |wx+b|=1,那么
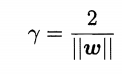
这就是边际d。
欲使边际最大,就是 maxd
注意,在训练过程中,我们使用的是全部样本,而不单是支持向量,而全部样本存在约束

综合表示就是 y(wx+b)>1,
那么目标为

最大转换为最小,方便计算

w加了平方,也是方便计算,不影响,w最小,w平方也就最小
以上就是SVM的基础理论。
拉格朗日乘子与对偶问题
其实上面的目标函数已经是个凸函数,可以用梯度下降等优化算法来求解,但是SVM使用了另一种优化算法,即拉格朗日对偶函数,
这部分比较麻烦,如果你不是专门研究SVM,没必要太纠结这块,因为即使你弄明白了,过一段时间就会忘记。
核函数
上面讲到用超平面来划分样本,但现实中很多问题是线性不可分的,此时不存在可划分类别的超平面。
对于这样的问题,需要将样本从原始空间映射到一个更高维的空间,使得样本在新的特征空间线性可分。
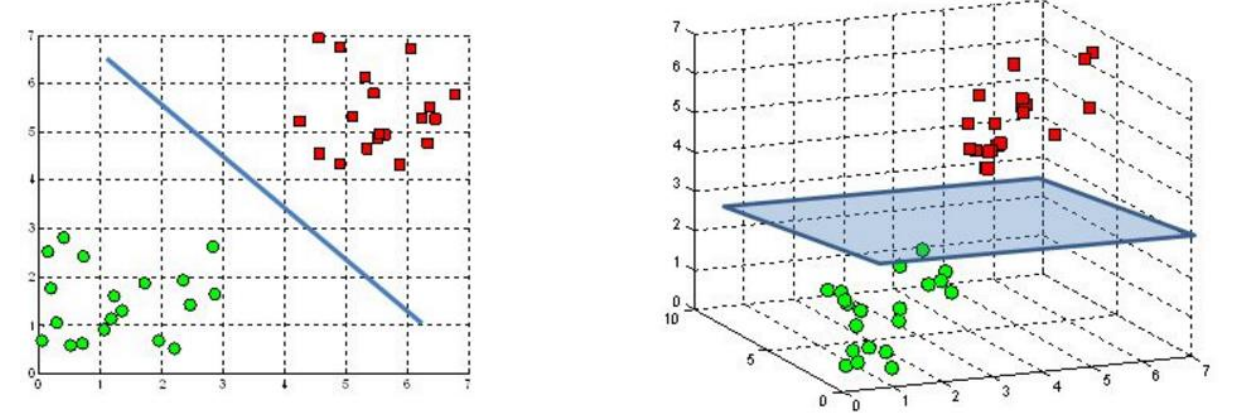
如果原始空间有限,那么一定存在一个高维空间使得样本可分。
这种映射其实就是一个函数,我们称之为核函数。
常用的核函数有

一般情况下会先用高斯核试试,但经验告诉我们,文本一般使用线性核。
核函数的计算也是可以简化的

SVM 处理非线性
svm 本身是个线性模型,包括 核函数 也是映射到高维空间的线性模型,那 smv 如何解决非线性问题呢?比如下面的那张图
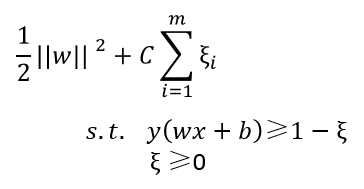
把约束条件稍微放宽一点, 就是允许有特例存在,
此处就是 允许 那些 只有一定概率 (wx+b<1) 为正的样本也被认为是正样本,从而把 决策边界 非线性的 绕过 边缘的几个特殊点;
我们可以稍微夸张一点,假设 ξ 取 无穷大,那么 1-ξ 就是无穷小,y(wx+b) 大于一个 无穷小的数,等于没约束,没有约束的情况下,决策边界自然想怎么画就怎么画咯,自然可以非线性;
软间隔与正则化
SVM总是在寻找超平面使得样本能够完全被分开,但是由于现实中数据杂质很多,完全分开很容易造成过拟合。
缓解这个问题的思路就是允许部分样本被错误划分,于是提出了“软间隔”的概念(相对有“硬间隔”的概念)
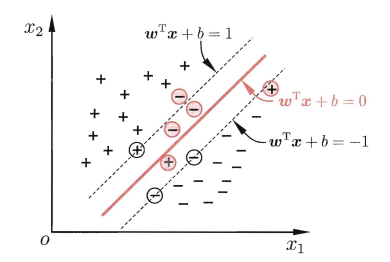
可以看到红色样本被错误划分
此时的红色样本实际为1(-1),预测为-1(1),已经不满足 y(wx+b)>1的约束条件,
那对应我们的目标函数怎么改呢?去掉约束吗?显然不能
在分类时,我们虽然容忍部分样本被错误划分,但是我们希望被错误划分的样本越少越好,也就是说我们希望大部分样本仍然满足约束条件。
目标函数可改为
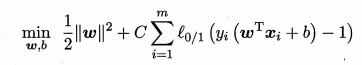
C是个>0的常数,也就是正则项系数,这里叫容忍系数
l0/1是“0/1损失函数”,就是上面的 ξ
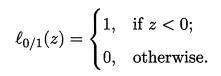
当样本被错误分类时,y(wx+b)<0,y(wx+b)-1<0,l0/1=1,
当样本被正确分类时,l0/1=0
要使目标函数最小,就要使后面那部分最小,然而当样本被错误划分时,后面为1,如果C很大,那么后面那部分就很大,显然不符合我们的目标,所以需要1尽可能少,也就是错误划分尽可能少。
当C无穷大时,就是不能错误划分,后面那部分是0,目标函数最小,也就是“硬间隔”。
所以C越大,模型越“精确”。
由于l0/1函数非凸,非连续,数学性质不太好,所以要用其他函数来替代它,称为“替代损失”
三种常用的替代损失函数
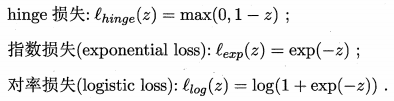
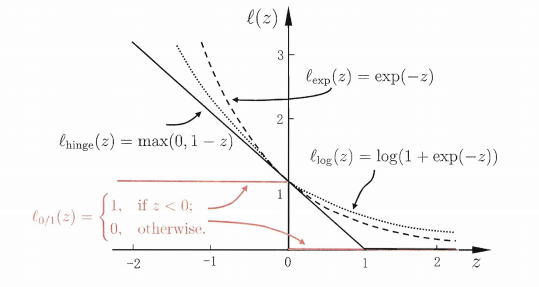
总结
SVM的理论十分复杂,上面只是介绍了冰山一角,有助于你在实际项目中完成调参工作。
SVM 可以解决 高维问题、非线性问题;
优点:
1. 能够解决小样本问题;
2. 相比于 神经网络,SVM考虑的是全局,全部样本,结果是全局最优;而 神经网络 可能陷入局部最优,因为 NN 是 batch 样本的学习,每次只学一点点;
3. 对异常值不敏感; 【参考 我的博客】
缺点:
1. 核函数计算复杂;
2. 在处理非线性问题时,选择合适的核函数很重要,缺乏通用的解决方案;
参考资料:
周志华 《机器学习》