https://zybuluo.com/ysner/note/1098815
标签(空格分隔): 网络流 最短路
知识点
这玩意儿大致的思路如下:
1.将源点到汇点中再补一条不与任何线段有交点的边(分界线)。这条边把外侧无限大的区域划分为了两部分,一部分为S面,另外一部分为T面。(其实把那两个面当成两个点就成了)
2.平面图的任何一条边一定只与两个面相连,将这两个边相连,权值为边的边权
此时S−>T的最短路就是原来平面图中的最小割。
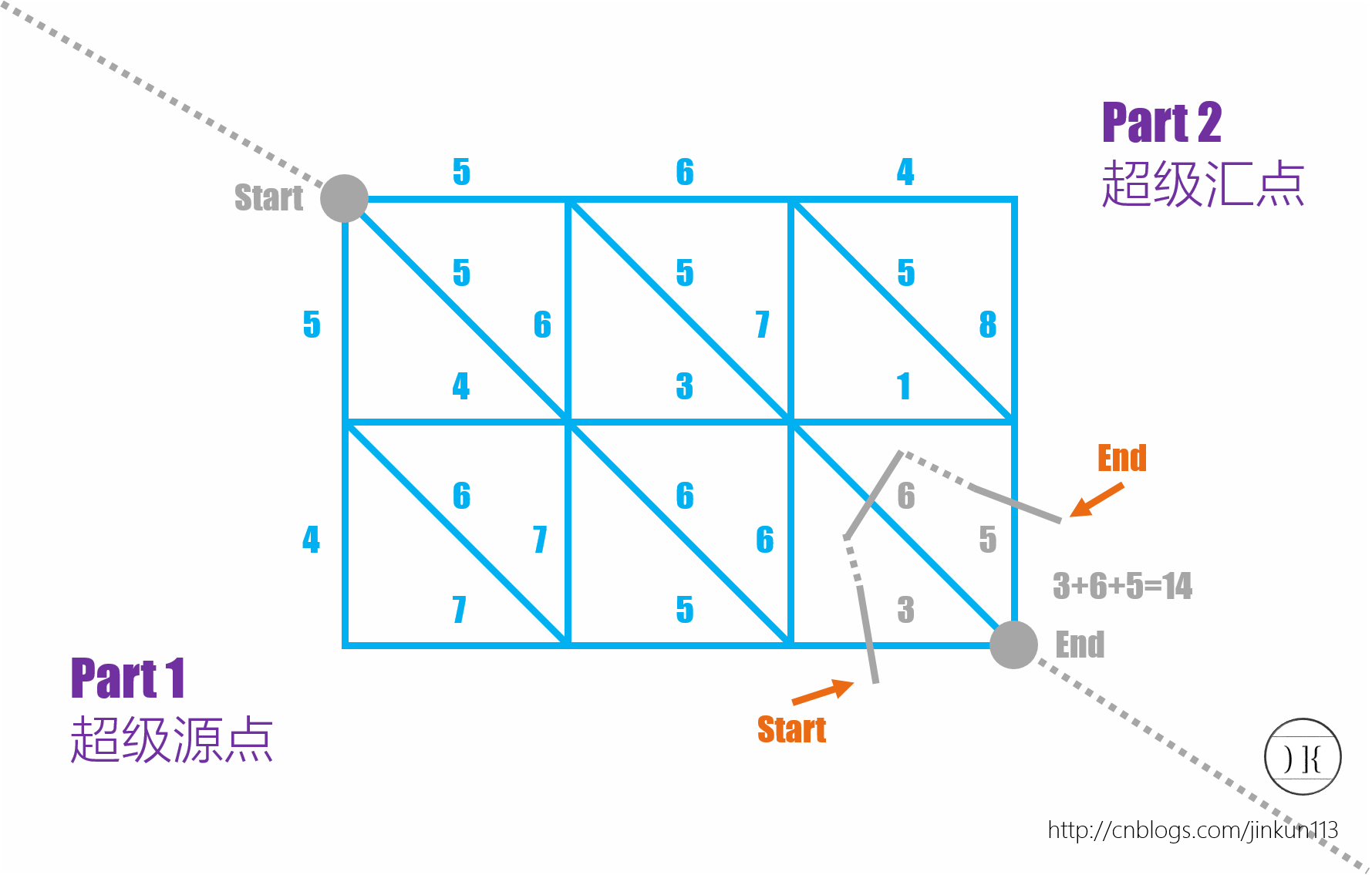
伪证如下:(感性yy一下即可)
如果在对偶图上走了一条边,必定将原图中的一条边给割开
考虑一条S−>T的路径,
一定沿着S平面割开了若干平面,使得S平面与T平面相连
因此,一条路径是原图中的一个割
割的大小就是路径的长度
因此,最小割就是对偶图上的最短路(用最小的代价把一个图分成两半)
例题
T1[BZOJ1001]狼抓兔子
建边过程如下:
fp(i,1,n)
{
fp(j,1,m-1)
{
re int u=S,v=T,w=gi();
if(i!=1) v=id[ysn-1][j];//啥,没到上界,可以向上界yy?
if(i!=n) u=id[ysn][j];//啥,没到下界,不是起点的地盘?
add(u,v,w);add(v,u,w);
}
ysn+=2;
}ysn=1;
fp(i,1,n-1)
{
fp(j,1,m)
{
re int u=S,v=T,w=gi();
if(j!=1) u=id[ysn][j-1];//啥,没到左界,不是起点的范围?
if(j!=m) v=id[ysn+1][j];//啥,不是终点的范围?
add(u,v,w);add(v,u,w);
}
ysn+=2;
}ysn=1;
fp(i,1,n-1)
{
fp(j,1,m-1)
{
re int u=id[ysn][j],v=id[ysn+1][j],w=gi();
add(u,v,w);add(v,u,w);//不会越界,无需讨论
}
ysn+=2;
}
就是把知识点那块模拟一遍。
T2[NOI2010]海拔
平面图求最小割
S=0,T=tot+1;
fp(i,0,n+1) id[i][0]=S,id[i][n+1]=T;
fp(i,0,n+1) id[0][i]=T,id[n+1][i]=S;
fp(i,1,n+1)
fp(j,1,n)
add(id[i][j],id[i-1][j],gi());
fp(i,1,n)
fp(j,1,n+1)
add(id[i][j-1],id[i][j],gi());
fp(i,1,n+1)
fp(j,1,n)
add(id[i-1][j],id[i][j],gi());
fp(i,1,n)
fp(j,1,n+1)
add(id[i][j],id[i][j-1],gi());
}
注意一下第一题那个建边方式可以简化,即把边界条件赋为超级点。
还有,割开一条边的方向随意。