
4*3 dot 3*2 == 4*2
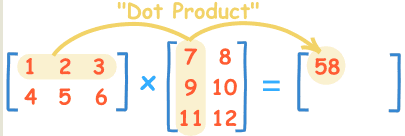
矩阵乘法条件:第一个矩阵的列(的个数)要等于第二个矩阵的行(个数) 2*3 dot 3*2 == 2*2

矩阵左乘 与 矩阵右乘
所谓矩阵左乘,其实就是矩阵放到乘号左边乘的意思。
举例如下:一个矩阵A有了,又来了一个矩阵B,B要和A矩阵左乘,那么是A*B,还是B*A呢?
B要放到左边进行相乘,就是左乘,也就是B*A。
再来个矩阵C,还是左乘,那就是C*B*A。
再来个矩阵D,还是左乘,就是D*C*B*A,……
所谓矩阵右乘,其实就是矩阵放到乘号右边乘的意思。
举例如下:一个矩阵A有了,又来了一个矩阵B,B要和A矩阵右乘,那么是A*B,还是B*A呢?
B要放到右边进行相乘,就是右乘,也就是A*B。
再来个矩阵C,还是右乘,那就是A*B*C。
再来个矩阵D,还是右乘,就是A*B*C*D,……


矩阵乘法的本质
1. 方程组的几何解释
“矩阵最初的目的,只是为线性方程组提供一个简写形式”[1]. 一个矩阵可以看成方程组的系数。我们来看这样一个方程组:
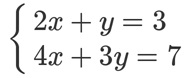
矩阵的最初目的,只是为线性方程组提供一个简写形式
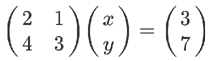
老实说,从上面这种写法,已经能看出矩阵乘法的规则了:系数矩阵第一行的2和1,各自与 x 和 y 的乘积之和,等于3。不过,这不算严格的证明,只是线性方程式转为矩阵的书写规则。
下面才是严格的证明。有三组未知数 x、y 和 t,其中 x 和 y 的关系如下。
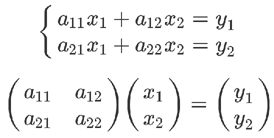
x 和 t 的关系如下。
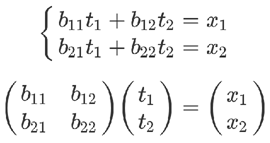
有了这两组方程式,就可以求 y 和 t 的关系。从矩阵来看,很显然,只要把第二个矩阵代入第一个矩阵即可。
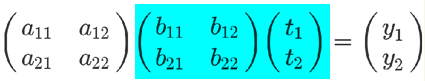
从方程式来看,也可以把第二个方程组代入第一个方程组。
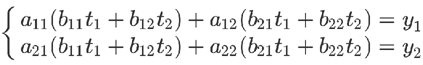
上面的方程组可以整理成下面的形式。
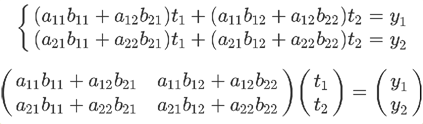
最后那个矩阵等式,与前面的矩阵等式一对照,就会得到下面的关系。
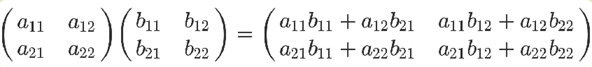
矩阵乘法的计算规则,从而得到证明。
再从图形上来看

在x,y坐标轴中,画出这两个方程对应的图像,如下图
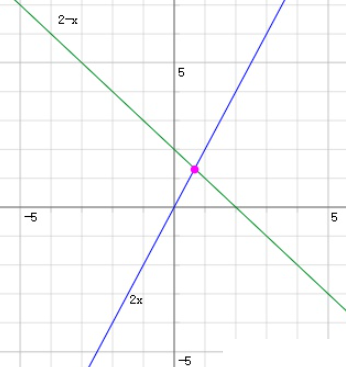
很容易发现,两条直线的交点就是方程组的解,也就是矩阵乘法的解。
从方程组的角度来解释,矩阵A可以看成方程组的系数,一个矩阵对应唯一的一个方程组。向量X左乘矩阵A就是方程组的简化记法。
显然向量X的各属性取不同的值,我们就得到了不同的组合,不同组合的结果会显示在结果矩阵中。如果X看成药材,那么A就可以看成药材的配比组合。不同的药材使用相同的配比阵(映射)A,得到几种不同的配方。
所以这里左乘的矩阵A也可以看成一个线性映射关系,矩阵中的每个值表示线性映射的映射系数(这个词乱扯的,大家明白什么意思就行).从数学意义上说,向量X左乘矩阵A就相当于对X进行线性映射