经典排序算法的总结及其Python实现

经典排序算法总结：

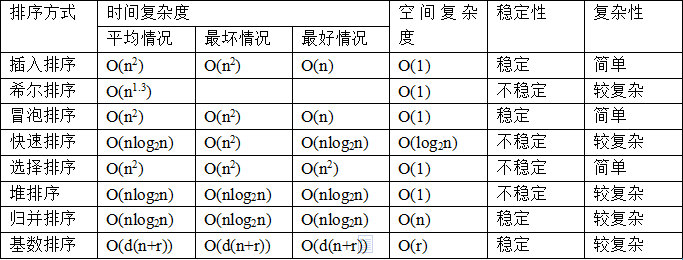
结论：

排序算法无绝对优劣之分。

不稳定的排序算法有：选择排序、希尔排序、快速排序、堆排序（口诀：“快速、选择、希尔、堆”）。其他排序算法均为稳定的排序算法。

第一趟排序后就能确定某个元素最终位置的有：选择排序、冒泡排序、快速排序、堆排序。

快速排序“偏爱”基本无序的序列。

希尔排序的关键在于步长的选择，希尔排序的时间复杂度和步长的选择有关。

快速排序之所以叫快速排序，并不代表它比堆排序、归并排序优良，在最好情况下它的渐进复杂度与堆排序、归并排序相同，只是它的常量系数比较小而已。

工程上的排序是综合排序，当数组较小时，选择插入排序；数组较大时，选择快速排序或其他O(n*log n)的排序。

 排序算法的Python实现

1.冒泡排序：

冒泡排序就是把小的元素往前调（或者把大的元素往后调）。注意是相邻的两个元素进行比较，而且是否需要交换也发生在这两个元素之间。

 实现代码：

## 1.冒泡排序
def bubbleSort(array):
    for times in range(len(array)-1,0,-1):
        for i in range(times):
            if array[i]>array[i+1]:
                temp=array[i]
                array[i]=array[i+1]
                array[i+1]=temp
    return array

2.选择排序:

选择排序即是给每个位置选择待排序元素中当前最小的元素。比如给第一个位置选择最小的，在剩余元素里面给第二个位置选择次小的，

依次类推，直到第n-1个元素，第n个元素不用选择了，因为只剩下它一个最大的元素了。

 

代码实现一：（推荐）

## 2.选择排序
def selectSort(array):
    for i in range(len(array)-1):
        small=i
        for j in range(i+1,len(array)):
            if array[j]<array[small]:
                small=j
        if small!=i:
            temp=array[small]
            array[small]=array[i]
            array[i]=temp
    return array

代码实现二：

# Finds the smallest value in an array
def findSmallest(arr):
  # Stores the smallest value
  smallest = arr[0]
  # Stores the index of the smallest value
  smallest_index = 0
  for i in range(1, len(arr)):
    if arr[i] < smallest:
      smallest = arr[i]
      smallest_index = i
  return smallest_index

# Sort array
def selectionSort(arr):
  newArr = []
  for i in range(len(arr)):
      # Finds the smallest element in the array and adds it to the new array
      smallest = findSmallest(arr)
      newArr.append(arr.pop(smallest))
  return newArr

print selectionSort([5, 3, 6, 2, 10])

3.插入排序：

插入排序是在一个已经有序的小序列的基础上，一次插入一个元素。当然，刚开始这个有序的小序列只有1个元素，也就是第一个元素（默认它有序）。

比较是从有序序列的末尾开始，也就是把待插入的元素和已经有序的最大者开始比起，如果比它大则直接插入在其后面。

否则一直往前找直到找到它该插入的位置。如果遇见一个与插入元素相等的，那么把待插入的元素放在相等元素的后面。

代码实现：

## 3. 插入排序
def insertSort(array):
    for i in range(1,len(array)):
        curr_val=array[i]
        pos=i
        while pos>0 and array[pos-1]>curr_val:
            array[pos]=array[pos-1]
            pos-=1
        array[pos]=curr_val
    return array

4.快速排序：

递归实现：

def quicksort(array):
  if len(array) < 2:
    # base case, arrays with 0 or 1 element are already "sorted"
    return array
  else:
    # recursive case
    pivot = array[0]
    # sub-array of all the elements less than the pivot
    less = [i for i in array[1:] if i <= pivot]
    # sub-array of all the elements greater than the pivot
    greater = [i for i in array[1:] if i > pivot]
    return quicksort(less) + [pivot] + quicksort(greater)

print quicksort([10, 5, 2, 3])

 非递归实现：写起来比较复杂。

5.归并排序

## 5.归并排序（递归实现）


def merge(left, right):
    res = []
    i, j = 0, 0
    while i < len(left) and j < len(right):
        if left[i] <= right[j]:
            res.append(left[i])
            i += 1
        else:
            res.append(right[j])
            j += 1
    res+=left[i:]
    res+=right[j:]

    return res

def mergeSort(array):
    if len(array)<=1:
        return array
    mid=len(array)//2
    left=mergeSort(array[:mid])
    right=mergeSort(array[mid:])

    return merge(left,right)

6.堆排序

## 6.堆排序(以最大堆为例)
def heapSort(array):
    first=len(array)//2-1
    # 从最后一个有孩子节点的节点开始调整最大堆
    for i in range(first,-1,-1):
        sift_down(array,i,len(array)-1)
    
    #将最大的值放到堆的最后一个位置，然后继续调整排序
    for j in range(len(array)-1,0,-1):
        array[0],array[j]=array[j],array[0]
        sift_down(array,0,j-1)
    return array

def sift_down(array,start,end):
    root=start
    # 从 root 开始对最大堆进行调整
    while True:
        # 左孩子节点
        child = 2*root+1
        if child>end:#如果超出范围，直接跳出
            break   
        # 左右孩子节点的值比较，选出大的那个
        if  child+1<=end and array[child+1]>array[child]:
            child+=1
        # 将大值调整到root的位置
        if array[root]<array[child]:
            array[root],array[child]=array[child],array[root]
            root=child
        else:
            break

7.希尔排序

## 7.希尔排序
def shellSort(array):
    gap=len(array)//2
    n=len(array)
    while gap>=1:
        for j in range(gap,n):
            i=j
            while i-gap>=0:
                if array[i]<array[i-gap]:
                    array[i], array[i-gap] = array[i-gap], array[i]
                    i-=gap
                else:
                    break
        gap//=2
        
    return array

8.基数排序

基数排序时借助于多关键字的思想进行排序的。

基数排序时一种按最低位优先法（Least Significant Digit First，LSD）排序的方法。它利用“分配”和“收集”两种运算实现排序。

基数排序的主要思想：假设单关键字ki可以分解为d个分量ki0,ki1,ki2,...,kid-1，其中最低位是kid-1,最高位是ki0,每个分量都有radix个取值，radix称为基数，比如整数614按radix=10可以分解成d=3个分量。基数排序先按最低位kid-1将序列R中的n个元素“分配”到0~radix-1个队列中，再按队列顺序“收集”到R，完成第一趟排序；第二趟排序按kid-2将序列R中的n个元素“分配”到0~radix-1个队列中，再按队列顺序“收集”到R，知道最后一趟按ki0“分配”和“收集”完成后，排序结束。

该算法对n个元素共进行d趟排序，每趟的“分配”需要将元素放到radix个队列中，“收集”需要收集n个元素，这样一趟“分配”和“收集”的时间为O(radix+n)，因此总的时间复杂度为O(d*(radix+n))

基数排序只有等到排序结束后才能确定元素的最终位置。它是稳定的排序方法。

9.计数排序

两者思想来源于桶排序 

它们不是局域比较的排序算法，时间复杂度为O(N),空间复杂度为O(M),M为选择的桶的数量，相当于以空间换时间。

 具体代码实现见参考链接

二分查找：

对于有序，或者某些部分有序的序列，查找满足题意的一个数，可以考虑使用二分查找（或者二分查找的变形）

经典的二分查找（查找有序数组中的某个值）代码如下：

# 二分查找
def binarySearch(array,val):
    start=0
    end=len(array)-1
    found=False
    #mid=(start+end)//2   
    while start<=end and not found:
        mid=start+(end-start)//2 #这样写不会溢出，更安全
        if array[mid]==val:
            found=True
        else:
            if array[mid]<val:
                start=mid+1
            else:
                end=mid-1
    return found  


print(binarySearch([0,1,2,8,13,17,19,32,42],9))

参考：

常见排序算法时间、空间复杂度及稳定性分析

桶排序&基数排序&计数排序：https://www.cnblogs.com/linxiyue/p/3555175.html

　　　　　　　　　　　　　 https://blog.csdn.net/xiaotao_1/article/details/78278622