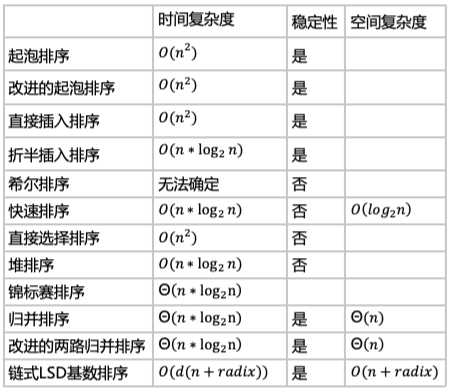
排序的时间开销可用算法执行中的数据比较次数和数据移动次数来衡量。
不稳定的排序方法往往是按照一定的间隔移动或交换记录对象的位置,从而可能导致具有相等排序码的不同对象的前后相对位置在排序前后颠倒过来。
稳定的排序方法往往在相邻的数据对象间比较排序码,如果发生逆序才交换,具有相等排序码的不同对象在排序前后不会颠倒。
一、起泡排序算法
1.基础起泡排序算法
n-1次起泡,第i次起泡从V[n-1]和V[n-2]到V[i]和V[i-1]共执行n-i次比较和交换操作,一共执行n(n-1)/2次。
数据比较次数与输入序列中各待排序的元素的初始排列无关,但数据交换次数与其有关。
如果在待排序码后面的若干排序码比前面的排序码小,则在起跑排序过程中,排序码可能向最终它应移动的位置相反方向移动。
typedef int T; void BubbleSort(T V[],int n){ for(int i=1; i<n; i++) //对数组V中n个元素进行排序,执行n-1次 for(int j=n-1; j>=i; j--) //第i次对V[n-1]和V[n-2]~v[i]和V[i-1]排序(n-i次比较与交换) if(V[j-1]>V[j]){ //逆序:前一个大于后一个 T temp=V[j-1]; V[j-1]=V[j]; V[j]=temp; } }
2.改进的起泡排序算法
在算法中增加标志exchange,用以标识本次起泡结果是否发生了逆序和交换。每次起泡前将exchange置为false,起泡过程中一旦发生交换就将exchange置为true,每次起泡后检查exchange,为false则已排序完成,直接return。
最好情况需要n-1次比较和0次交换,最差情况下需要n(n-1)/2次比较,3n(n-1)/2次交换。
因此一般情况下,排序算法大约需要n2/2次比较和交换操作。
typedef int T; void BubbleSort(T V[],int n){ bool exchange; //增加标志检测本次起泡排序是否发生逆序和交换 for(int i=1; i<n; i++){ exchange=false; //每次起泡前把exchange置为false for(int j=n-1; j>=1; j--) if(V[j-1]>V[j]){ T temp=V[j-1]; V[j-1]=V[j]; V[j]=temp; exchange=true; } if(!exchange) return ; //本次无逆序,停止处理 } }
3.其它一些起泡排序算法
奇数次排序从前往后,偶数次排序从后往前。也利用exchange进行控制。
void shaker_Sort(T V[],int n){ int i=1,j; bool exchange; do{ //起泡排序总次数不大于n-1 exchange = false; for(j=i-1; j<n-i; j++){ if V[j]>V[j+1]{ Swap(j,j+1); exchange=true; } } if(!exchange) break; exchange=false; for(j=n-i-1; j>i-1; j--){ if(L[j-1]>L[j]){ L.Swap(j-1,j); exchange=true; } } i++; }while(exchange) }
奇数次排序时从前往后,每次对两个元素进行交换时把左边那个元素的位置记录了下来,最后修改high。
偶数次排序从后往前,每次对两个元素进行交换时把右边那个元素的位置记录了下来,最后修改high,修改low。
可以认为low左边的和hih右边的元素都已排序完成,low>=high时排序完成。
void shaker_Sort(T V[],int n){ int low=0,high=n-1,i,j; while(low<high){ j=low; //记忆元素最后交换位置 for(i=low; i<high; i++) if(V[i]>V[i+1]){ Swap(i,i+1); j=i; //记忆右边最后发生交换位置 } high=j; for(i=high; i>low; i--){ if(V[i-1]>V[i]){ Swap(i-1,i); j=i; } } low=j; } }
二、插入排序
1.直接插入排序
n-1次插入,排序码比较次数和元素移动次数与元素排列码的初始排列有关。
最好情况下,每次只需要将插入元素和前面的有序元素序列最后一个元素的排序码比较1次,即总比较n-1次移动0次。
最差情况下,第i次插入,需要比较i次、移动i+2次,总比较次数KCN=n(n-1)/2,总移动次数RMN=(n+4)(n-1)/2。
平均情况下排序码比较次数和元素移动次数约n2/2。因此直接插入排序的时间复杂度为O(n2)。
template <class T> void InsertSort(dataList<T>& L,const int left,const int right){ Element<T> temp; int i,j; for(i=left+1; i<=right; i++) if(L[i]<L[i-1]){ temp=L[i]; j=i-1; do{ L[j+1]=L[j]; j--; }while(j>=left && temp<L[j]); //如果L[left]也比temp大,j最后会变为left-1 L[j+1]=temp; } }
2.折半插入排序/二分法插入排序
是一种稳定的排序方法。
总排序码比较次数比直接插入排序的最好情况差、最差情况好。
元素初始排列有序或者接近有序时,折半插入排序的排序码比较次数更多。折半插入排序的元素移动次序同样依赖元素初始排列。
将n个元素进行折半插入排序的排序码比较次数约为n·log2n。
template <class T> void BinaryInsertSort(dataList<T>& L,const int left,const int right){ Element<T> temp; int i,low,high,middle,k; for(i=left+1; i<=right; i++){ temp=L[i]; low=left; high=i-1; while(low<=high){ //即使i==left+1时,low==high。直到low==middle==high的时候才会结束递归 middle=(low+high)/2; if(temp<L[middle]) high=middle-1; else low=middle+1; //如果temp=L[middle],low=middle+1,temp插入到low位置即可 } for(k=i-1; k>=low; k--) L[k+1]=L[k]; L[low]=temp; } }
3.希尔排序/缩小增量排序

template <class T> void Shellsort(dataList<T>& L,const int left,const int right){ int i,j,gap=right-left+1; Element<T> temp; do{ gap=gap/3+1; for(i=left+gap; i<=right; i++) if(L[i]<L[i-gap]){ //子序列采用直接插入排序。若L[i]>L[i-gap],x无需进行任何操作 temp=L[i]; j=i-gap; do{ L[j+gap]=L[j]; j=j-gap; }while(j>=left && temp<L[j]); L[j+gap]=temp; } }while(gap>1); }
三、快速排序/分区排序

template <class T> void QuickSort(dataList<T>& L,const int left,const int right){ if(left<right){ int pivotpos=L.Partition(left,right); QuickSort(L,left,pivotpos-1); QuickSort(L,pivotpos+1,right); } } template <class T> int dataList<T>::Partition(const int low,const int high){ int pivotpos=low; //基准元素位置 Element<T> pivot=Vector[low]; //基准元素值 for(int i=low+1; i<=high; i++) if(Vector[i]<pivot){ pivotpos++; //pivotpos始终指向小于基准元素的最后一个元素位置 if(pivotpos!=i) Swap(Vector[pivotpos],Vector[i]); } Vector[low]=Vector[pivotpos];Vector[pivotpos]=pivot; //最后把位于low的基准元素pivot和位于pivotpos的小于基准元素的最后一个元素互换 return pivotpos; //返回基准元素的位置 } template <class T,class E> void quickSorting(dataList<T>& L){//利用栈进行快排 struct Snode{int low,high;} Snode temp; Stack<SNode> S; int left, right, mid; temple.low=0; temp.high=L.Length()-1; S.Push(temp); while (!S.isEmpty()) { S.pop(temp); left=temp.low; right=temp.high; mid=L.Partition(left,right); //划分为两个子序列 if(mid-left<=right-mid){ //先把较短的子序列入栈 if(mid+1<right){ temp.low=mid+1; temp.high=right; S.Push(temp); } right=mid-1; } else if(mid-left>right-mid){ if(left<mid-1){ temp.low=left; temp.high=mid-1; S.Push(temp); } left=mid+1; } if(left<right){ //再把较长的子序列入栈 temp.low=left; temp.high=right; S.Push(temp); } } }
四、选择排序
1.直接选择排序
n-1次选择,每一次在后面n-i+1个待排序元素中选出排序码最小的元素,作为有序元素序列的第i个元素
排序码比较次数KCN与元素初始排列无关,第i次选择具有最小排序码元素所需的比较次数总是n-i次,共计n(n-1)/2次
元素移动次数与元素序列初始排列有关,最好情况为RMN=0,最差情况RMN=3(n-1)。
是一种不稳定的排序方法。
比较简单且执行时间固定,适用于元素规模大、排序码小的序列(这类序列移动操作所花时间远大于比较操作)。
template <class T> void SelectSort(dataList<T>& L,const int left,const int right){ for(int i=left; i<right; i++){ int k=i; for(int j=i+1; j<=right; j++){ if(L[j]<L[k]) k=j; //当前具有最小排序码的元素 } if(k!=i) Swap(L[i],L[k]); //交换 } }
2.锦标赛排序
https://www.cnblogs.com/yangyuliufeng/p/10720113.html
3.堆排序

template <class T> struct Element{ T key; field otherdata; Element<T>& operator=(Element<T>& x){ key=x.key; otherdata=x.otherdata; } bool operator>=(Element<T>& x){return key>=x.key;} bool operator<(Element<T>& x){return key<x.key;} } template <class T> class MaxHeap{ public: MaxHeap(int sz=DefaultSize); MaxHeap(Element arr[],int n); ~MaxHeap(){delete []heap}; bool Insert(Element& x); bool Remove(Element& x); bool IsEmpty()const{return currentSize==0;} bool IsFull()const{return currentSize==maxHeapSize;} private: Element<T> *heap; int currentSize; int maxHeapSize; void siftDown(const int start,const int m); //从start到m自顶向下调整 void siftUp(int start); //从start到0自底向上调整 Swap(const int i,const int j){ Element<T> tmp=heap[i]; heap[i]=heap[j]; heap[j]=temp; } } template <class T> void MaxHeap<T>::siftDown(const int start,const int m){ //私有函数,从结点start到m为止,自上向下比较,如果子女的值小于双亲结点的值则交换,这样将一个集合局部调整为最大堆 int i=start; int j=2*i+1; //j是i的左子女 Element<T,E> temp=heap[i]; while(j<=m){ if(j<m && heap[j]<heap[j+1]) j++; //让child指向两子女中的大者 if(temp>=heap[j]) break; else{ heap[i]=heap[j]; i=j;j=2*j+1; //i下降到子女位置 } } heap[i]=temp; } template <class T> void HeapSort(maxHeap<T>& H){ for(int i=(currentSize-2)/2; i>=0; i--) //将表转换成堆 siftDown(i,currentSize-1); for (i=currentSize-1; i>=0; i--) { Swap(0,i); SiftDown(0,i-1); //重建最大堆 } }
五、归并排序

template <class T> void mergeSort(dataList<T>& L,dataList<T>& L2,int left,int right){ if(left>=right) return; int mid=(left+right)/2; mergeSort(L,L2,left,mid); //递归直到left=mid的时候不进行任何操作直接return mergeSort(L,L2,mid+1,right); //递归直到mid+1=right的时候不进行任何操作直接return merge(L,L2,left,mid,right); } template <class T> void merge(dataList<T>& L1,dataList<T>& L2,const int left,const int mid,const int right){ //L1.Vector[left:mid]与L1.Vector[mid+1:right]是两个有序表,归并为L1.Vector[left:right] for(int k=left; k<=right; k++) L2[k]=L1[k]; //先都放到L2,归并后再放到L1 int s1=left,s2=mid+1; //检测指针 int t=left; //归并后在L1中的当前存放指针 while(s1<=mid && s2<=right) if(L2[s1]<=L2[s2]) L1[t++]=L2[s1++]; else L1[t++]=L2[s2++]; while(s1<=mid) L1[t++]=L2[s1++]; while(s2<=right) L1[t++]=L2[s2++]; }
在复制到辅助数组L2时可以把第二个有序表的元素顺序逆转,这样L2两端元素小中间元素大,检查指针s1和s2初始为left和right,两个待归并的表从两端开始处理向中间归并,两个表的尾端互为监视哨,也可以省去检查子序列是否结束的判断。
void improvedMerge(dataList<T>& L1,dataList<T>& L2,const int left,const int mid,const int right){ int s1=left,s2=right; //检测指针 int t=left; //存放指针 int k; for(k=left,k<=mid;k++) L2[k]=L1[K]; for(k=mid+1;k<=right;k++) L2[right+mid+1-k]=L1[k]; while (t<=right) { if(L2[s1]<=L2[s2]) L1[t++]=L2[s1++]; else L1[t++]=L2[s2--]; } } template <class T> void doSort(dataList<T>& L,dataList<T>& L2,int left,int right){ if(left<=right) return; if(right-left+1<M) return; //序列长度小于M跳出递归 int mid=(left+right)/2; doSort(L,L2,left,mid); doSort(L,L2,mid+1,right); improvedMerge(L,L2,left,mid,right); } template <class T> void mergeSort(dataList<T>& L,dataList<T>& L2,int left,int right){ doSort(L,L2,left,right); insert(L,left,right); //对排序结果再做插入排序 }
同理,链表的归并排序为:
template <class T,class E> void Merge_sort(List<E,T>& L){ LinkNode<T,E> *q,*h,*p; Queue<LinkNode<T,E>*> Q; if(L.first==NULL) return; h=L.first; Q.Enquench(h); while (1) { p=h->link; while (p!=NULL && h->data<=p->data) { //在链表中寻找一段有序链表 h=p; p=p->link; } h->link=NULL; //前一段有序链表收尾 h=p; //继续搜索下一段有序链表 if (h!=NULL) Q.Enquench(h); else break; } while (!Q.isEmpty()) { Q.getFront(p); if (Q.isEmpty()) {break;} Q.getFront(q); Merge(p,q,h); Q.Enquench(h); } L.first=h; } template <class T,class E> void Merge(LinkNode<T,E> *ha, LinkNode<T,E> *hb, LinkNode<T,E> *&hc){ LinkNode<T,E> *pa,*pb,*pc; if(ha->data<=hb->data){ hc=ha; pa=ha->link; pb=hb; } else{ hc=hb; pb=hb->link; pa=ha; } pc=hc; while(pa!=NULL && pb!=NULL) if(pa->data<=pb->data){ pc->link=pa; pc=pa; pa=pa->link; } else{ pc->link=pb; pc=pb; pb=pb->link; } if(pa!=NULL) pc->link=pa; else pc->link=pb; }
六、分配排序
1.桶式排序
将元素分配至各个桶中的操作的时间复杂度为O(n),每个子序列排序的时间与子序列排序算法有关。
整个桶式排序总的时间复杂度也为O(n),对于均匀分布的元素序列,时间开销线性增长。
2.基数排序
利用多排序码排序实现对单个排序码排序。
radix为符号数,每个排序码有d位。
(1)MSD(最高位优先)基数排序
最高位优先:是一个递归过程,首先根据最高位排序码进行排序,得到若干元素组。分别对每组元素依据次高位排序码进行排序,得到更小的分组。
当待排序的排序码大小只取决于高位的少数几位而与大多数低位无关时,MSD比LSD效率更高。
(2)LSD(最低位优先)基数排序
最低位优先:先依据最低位排序码进行排序,然后依据次低位优先码进行排序。
链式LSD基数排序:
对于有n个元素的链表,执行while循环进行n次分配,把n个元素分配到radix个链表中去。
执行for循环进行radix次收集,从每个队列中把元素收集起来按顺序重新链接成一张链表。
每个排序码有d位,需要进行d次分配和收集,总时间复杂度为O(d(n+radix))
radix一定时,对于元素个数较多而排序码位数较少的情况(例如非负整数),使用链式基数排序较好,它是稳定的排序方法
但其不适合浮点数排序。
const int radix=10; template <class T> void Sort(staticList<T>& L,int d){ int rear[radix],front[radix]; //radix个桶,每个桶设置两个队列指针,分别指示队头和队尾 int i,j,k,last,current,n=L.Length(); for(i=0; i<n; i++) L[i].link=i+1; L[n].link=0; //静态链表初始化,形成循环链表 current=1; for (i=d; i>=1; i--) { //每个排序码有d位,进行d次循环,从第d位到第1位依次进行分配和收集 for (j=0; j<radix; j++) front[j]=0; //每次循环前重置front指针 while (current!=0) { k=getDigit(L[current],i); //取当前检测元素的第i个排序码 if(front[k]==0) front[k]=current; else L[rear[k]].link=current; rear[k]=current; current=L[current].link; //检测下一个元素 } j=0; while (front[j]==0) j++; //跳过空队列 L[0].link=current=front[j]; //第1个非空队列第j队列的队头成为新链表的表头。current变为了新静态链表表头的位置。 last=rear[j]; for(k=j+1; k<radix; k++) if(front[k]!=0){ L[last].link=front[k]; last=rear[k]; } L[last].link=0; //新链表表尾 } }
基于数组的LSD基数排序:
需要计数器count[radix]和一个与待排序元素组同样大小的辅助数组auxArray[n]。