离散数学知识点总结（9）-树

一、无向树和有向树

对于任何无向图，若图中不存在简单回路，则 m≤n-1 

无向图是无向树的四个条件互相等价：连通、不存在简单回路、m=n-1满足至少2个

　　　　　　　　　　　　　　　　　每一对相异顶点之间存在唯一的简单道路 

　　　　　　　　　　　　　　　　   极小连通（每一条边都是桥）

  　　　　　　　　　　　　　　　　 极大无圈

因此无向树必定不含重边和自环，一定是简单图，一定是平面图。

无向树中度数为1的顶点称为叶子，度数大于1的顶点称为分枝点。 

平凡树：一阶简单图，既无叶子又无分枝点

任何非平凡树至少有2个叶子顶点

证明：设n(n≥2) 阶无向连通图G的边数满足m=n-1，设图中度数为1的顶点数为t，则2m=deg(v₁)+...+dev(v_n)≥t+2(n-t)，得t≥2

          或者设无向树中存在着a_i个度为i的顶点，a₁+2a₂+...=2m，a₁+a₂+...=n=m+1，故叶子数=a₃+2a₄+3a₅+...+2≥2

森林：不含任何简单回路的图。森林的每个连通分支都是树

二、有向树和根树

有向树：不考虑边的方向时是一棵无向树的有向图

根树：只有一个入度为0的顶点，其它顶点入度均为1的有向树

根树中出度为0的顶点称为叶子，出度大于0的顶点称为分枝点

在根树中，从根到任一其它顶点都存在唯一的简单道路

以v为根的根树：有向图中存在顶点v，使得从v到图中任意其它顶点都存在唯一简单道路，而且不存在从v到v的简单回路

在根树中，由根到顶点v的道路长度称作v的层数（level） ；所有顶点的层数的最大值称为根树的高度（height）

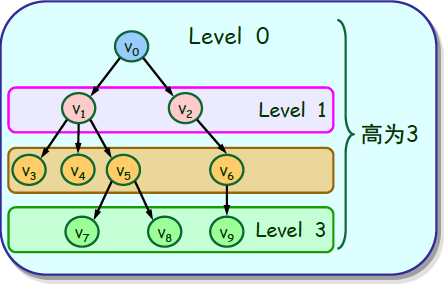
若T的每个分支点最多m个儿子，则称T为m叉树；若其每个分支点都恰好m个儿子，则称T为m叉正则树 

正则m叉树，其叶子数为t，分枝点数为i，则所有顶点出度之和为mi=所有顶点的入度之和t+i-1，故(m-1)i=t-1

三、标号树  

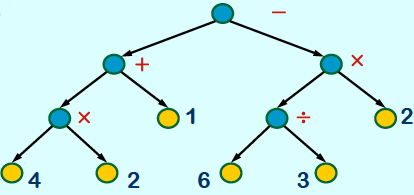
• 前序遍历结果-+×421×÷632称作前缀表示、波兰式

将波兰式压栈，当插入到×42时将其替换为8

• 后序遍历结果42×1+63÷2×-称作后缀表示、逆波兰式

将波兰式压栈，当插入到42×时将其替换为8

• 中序遍历表达式4×2+1-6÷3×2称作中缀表示

由前缀表示或后缀表示可以唯一构造表示运算式的有序树，但是由中缀表示则不行 

此外还有一些关于遍历、哈夫曼编码的知识点，数据结构中就有