解题报告 之 HDU5317 RGCDQ

解题报告 之 HDU5317 RGCDQ

Description

Mr. Hdu is interested in Greatest Common Divisor (GCD). He wants to find more and more interesting things about GCD. Today He comes up with Range Greatest Common Divisor Query (RGCDQ). What’s RGCDQ? Please let me explain it to you gradually. For a positive integer x, F(x) indicates the number of kind of prime factor of x. For example F(2)=1. F(10)=2, because 10=2*5. F(12)=2, because 12=2*2*3, there are two kinds of prime factor. For each query, we will get an interval [L, R], Hdu wants to know  

 

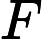
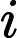
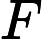
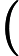
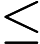
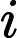
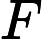
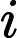
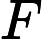
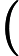
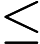
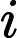
Input

There are multiple queries. In the first line of the input file there is an integer T indicates the number of queries. 
In the next T lines, each line contains L, R which is mentioned above. 

All input items are integers. 
1<= T <= 1000000 
2<=L < R<=1000000 

 

Output

For each query，output the answer in a single line. 
See the sample for more details. 

 

Sample Input

2
2 3
3 5 

 

Sample Output

1
1 

题目大意：首先定义F(x)为 x 的质因子的种类数，比方20=2*2*5，那么F(x)=2 。如今给出区间[L,R]，问你该区间内中随意两个数的GCD的最大值是多少？

分析：首先无论是不是一開始就想到要怎么做，肯定要完毕的是把每一个数的F(x)求出来，这里非常自然的想到了筛法。

对于每一个质数，它的每一个倍数的质因子数都++。然后扫一遍之后就完毕了F(x)的更新。筛法详细见相关文章一。

好筛完了F(x)，那么怎么求最大的GCD呢。一開始发现肯定不能暴力来，所以纠结了一会儿。然后后来看调试发现F(x)的值全都是1，2，3，4。。。这样的小数。然后统计出来一看最大的F(x)才仅仅有7。那么这个问题就迎刃而解了。直接扫一遍更新到R为止每种F(x)有多少个。然后区间给定之后依次推断各种情形就可以。

上代码：

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;

typedef long long ll;
const int MAXN = 1e6 + 10;

int isprime[MAXN];
int f[MAXN];
int dis[MAXN][8];

void ini()
{
	memset( isprime, -1, sizeof isprime );
	memset( f, 0, sizeof f );
	memset( dis, 0, sizeof dis );

	for(int i = 2; i < MAXN; i++)
	{
		if(!isprime[i]) continue;
		for(int j = i; j < MAXN; j += i)
		{
			f[j]++;
			isprime[j] = 0;
		}
	}

	for(int i = 2; i < MAXN; i++)
	{
		for(int j = 1; j <= 7; j++)
		{
			dis[i][j] = dis[i - 1][j];
		}
		dis[i][f[i]]++;
	}

}

int main()
{
	ini();
	int kase;
	scanf( "%d", &kase );

	while(kase--)
	{
		int l, r;
		scanf( "%d%d", &l, &r );

		int ma = 0;
		for(int i = 7; i >= 2;i--)
		{
			if(dis[r][i] - dis[l - 1][i] >= 2) 
			{
				ma = i;
				break;
			}
		}

		if(dis[r][6] - dis[l - 1][6] >= 1 && dis[r][2] - dis[l - 1][2] >= 1)
		{
			ma = max( ma, 3 );
		}

		if(dis[r][6] - dis[l - 1][6] >= 1 && dis[r][3] - dis[l - 1][3] >= 1|| dis[r][4] - dis[l - 1][4] >= 1 && dis[r][2] - dis[l - 1][2] >= 1)
		{
			ma = max( ma, 2 );
		}

		ma = max( ma, 1 );
		printf( "%d
", ma );

	}
	return 0;
}