(最短路径算法整理)dijkstra、floyd、bellman-ford、spfa算法模板的整理与介绍

 这一篇博客以一些OJ上的题目为载体。整理一下最短路径算法。会陆续的更新。。。

   

一、多源最短路算法——floyd算法

       floyd算法主要用于求随意两点间的最短路径。也成最短最短路径问题。

       核心代码：

       

/**
 *floyd算法
 */
void floyd() {
	int i, j, k;
	for (k = 1; k <= n; ++k) {//遍历全部的中间点
		for (i = 1; i <= n; ++i) {//遍历全部的起点
			for (j = 1; j <= n; ++j) {//遍历全部的终点
				if (e[i][j] > e[i][k] + e[k][j]) {//假设当前i-->j的距离大于i-->k--->j的距离之和
					e[i][j] = e[i][k] + e[k][j];//更新从i--->j的最短路径
				}
			}
		}
	}
}

    时间复杂度:O(N^3）

    不能使用的情况：边中含有负权值

例题：

1、WIKIOI 1077  多源最短路 

分析：这道题是floyd的裸题。

大家仅仅要理解了floyd的思想以后，基本非常快就能解答出来了。唯一须要注意的地方就是

这道题的map[][]矩阵中的顶点默认是从1開始。

假设顶点是从0開始算的须要做一下处理：printf("%d ",map[a-1][b-1]);

/*
 * 1077.cpp
 *
 *  Created on: 2014年5月23日
 *      Author: pc
 */

#include <iostream>
#include <cstdio>

using namespace std;

const int maxn = 105;
int e[maxn][maxn];
int n;

const int inf = 99999999;

void initial() {
	int i, j;
	for (i = 1; i <= n; ++i) {
		for (j = 1; j <= n; ++j) {
			if (i == j) {
				e[i][j] = 0;
			} else {
				e[i][j] = inf;
			}
		}
	}
}

/**
 *floyd算法
 */
void floyd() {
	int i, j, k;
	for (k = 1; k <= n; ++k) {//遍历全部的中间点
		for (i = 1; i <= n; ++i) {//遍历全部的起点
			for (j = 1; j <= n; ++j) {//遍历全部的终点
				if (e[i][j] > e[i][k] + e[k][j]) {//假设当前i-->j的距离大于i-->k--->j的距离之和
					e[i][j] = e[i][k] + e[k][j];//更新从i--->j的最短路径
				}
			}
		}
	}
}

int main() {
	while (scanf("%d", &n) != EOF) {

		initial();

		int i, j;
		for (i = 1; i <= n; ++i) {
			for (j = 1; j <= n; ++j) {
				scanf("%d", &e[i][j]);
			}
		}

		floyd();
		int q;
		scanf("%d", &q);
		while (q--) {
			int a, b;
			scanf("%d %d", &a, &b);

			printf("%d
", e[a][b]);
		}

	}

	return 0;
}

下面是自己再次做这道题的时候的代码：

/*
 * WIKIOI_1077.cpp
 *
 *  Created on: 2014年9月6日
 *      Author: pc
 */


#include <iostream>
#include <cstdio>

const int maxn = 105;
const int inf = 999999;

int map[maxn][maxn];

void initial(int n){
	int i;
	int j;
	for(i = 0 ; i < n ; ++i){
		for(j = 0 ; j < n ; ++j){
			if(i == j){
				map[i][j] = 0;
			}else{
				map[i][j] =  inf;
			}
		}
	}
}

void floyd(int n){
	int i;
	int j;
	int k;
	for(k = 0 ; k < n ; ++k){//顶点从0開始算》。
。
		for(i = 0 ; i < n ; ++i){
			for(j = 0 ; j < n ; ++j){
				if(map[i][j] > map[i][k] + map[k][j]){
					map[i][j] = map[i][k] + map[k][j];
				}
			}
		}
	}
}


int main(){
	int n;
	scanf("%d",&n);

	initial(n);

	int i;
	int j;
	for(i = 0 ; i < n ; ++i){
		for(j = 0 ; j < n ; ++j){
			int c;
			scanf("%d",&c);
			map[i][j] = c;
		}
	}

	floyd(n);

	int q;
	scanf("%d",&q);
	while(q--){
		int a,b;
		scanf("%d %d",&a,&b);
		printf("%d
",map[a-1][b-1]);
	}

	return 0;
}

二、单源最短路径算法——dijkstra

       1、思想描写叙述：当Q(一開始为全部节点的集合)非空时。不断地将Q中的最小值u取出，然后放到S（最短路径的节点的集合）集合中，然后遍历全部与u邻接的边。假设能够进行松弛，则对便进行对应的松弛。

。

。

       2、实现

 

/**
 * 返回从v---->到target的最短路径
 */
int dijkstra(int v){
	int i;
	for(i = 1 ; i <= n ; ++i){//初始化
		s[i] = 0;//一開始。全部的点均为被訪问过
		dis[i] = map[v][i];
	}
        dis[v] = 0; 
        s[v] = true;
	for(i = 1 ; i < n ; ++i){
		int min = inf;
		int pos;

		int j;
		for(j = 1 ; j <= n ; ++j){//寻找眼下的最短路径的最小点
			if(!s[j] && dis[j] < min){
				min = dis[j];
				pos = j;
			}
		}

		s[pos] = 1;

		for(j = 1 ; j <= n ; j++){//遍历u的全部的邻接的边
			if(!s[j] && dis[j] > dis[pos] + map[pos][j]){
				dis[j] = dis[pos] + map[pos][j];//对边进行松弛
			}
		}
	}


	return dis[target];
}

        3、基本结构

    

int s[maxn];//用来记录某一点是否被訪问过
int map[maxn][maxn];//地图
int dis[maxn];//从原点到某一个点的最短距离(一開始是估算距离)

4、条件：使用dijkstra解决的题目一般有下面的特征：

给出点的数目、边的数目、起点和终点、边的信息(,而且边不包括负边权的值).求从起点到终点的最短路径的距离

起点：用于dijkstra(int v)中的v

终点：用于return dis[target]中的target

边的信息：用于初始化map[][]

5、算法运行过程分析

 如图：求0点到其它点的最短路径。

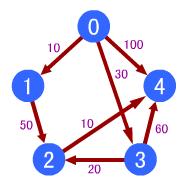
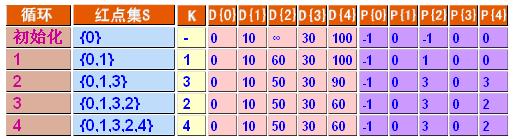
(1)開始时，s1={v0},s2={v1,v2,v3,v4}，v0到各点的最短路径是{0,10,&,30,100};
(2)在还未进入s1的顶点之中。最短路径为v1。因此s1={v0,v1},因为v1到v2有路径，因此v0到各点的最短路径更新为{0,10,60,30,100};
(3)在还未进入s1的顶点之中。最短路径为v3，因此s1={v0,v1,v3},因为v3到v2、v4有路径，因此v0到各点的最短路径更新为{0,10,50,30,90}；
(4)在还未进入s1的顶点之中。最短路径为v2，因此s1={v0,v1,v3,v2},因为v2到v4有路径。因此v0到各点的最短路径更新为{0,10,50,30,60};

例题：

1、NEFU 207 最小树

题目与分析：

这一道题。抽象一下，描写叙述例如以下：“求从a到b的最短路径的距离”。

floyd：解决多源最短路径问题。求随意两个点之间的最短路径。这当然也就包括了“从a到b的这样的情况”。所以这道题也能够使用floyd来解决

dijkstra：解决单源最短路径问题 。最典型的就是解决“从a到b的最短路径的距离”的这样的问题了。

下面分别给出这两种算法的解题方法

1）使用floyd

/*
 * NEFU_207.cpp
 *
 *  Created on: 2014年5月27日
 *      Author: pc
 */

#include <iostream>
#include <cstdio>

using namespace std;

const int maxn = 105;
const int inf = 99999999;
int e[maxn][maxn];

int n,m;

void initial(){
	int i;
	int j;
	for(i = 1 ; i <= n ; ++i){
		for(j = 1 ; j <= n ; ++j){
			if(i == j){
				e[i][j] = 0;
			}else{
				e[i][j] = inf;
			}
		}
	}
}


void floyd(){
	int i;
	int j;
	int k;

	for(k = 1 ; k <= n ; ++k){
		for(i = 1 ; i <= n ; ++i){
			for(j = 1 ; j <= n ; ++j){
				if(e[i][j] > e[i][k] + e[k][j]){
					e[i][j] = e[i][k] + e[k][j];
				}
			}
		}
	}
}


int main(){
	while(scanf("%d%d",&n,&m)!=EOF){
		initial();

		int i;
		for(i = 1 ; i <= m ; ++i){
			int a,b,c;
		    scanf("%d%d%d",&a,&b,&c);
		    e[a][b] = e[b][a] = c;
		}

		floyd();

		printf("%d
",e[1][n]);
	}

	return 0;
}

2）使用dijkstra

/*
 * NEFU_207.cpp
 *
 *  Created on: 2014年5月27日
 *      Author: pc
 */


#include <iostream>
#include <cstdio>

using namespace std;

const int maxn = 105;
const int inf = 9999999;

int s[maxn];//用来记录某一点是否被訪问过
int map[maxn][maxn];//地图
int dis[maxn];//从原点到某一个点的最短距离(一開始是估算距离)

int n;
int target;

/**
 * 返回从v---->到target的最短路径
 */
int dijkstra(int v){
	int i;
	for(i = 1 ; i <= n ; ++i){//初始化
		s[i] = 0;//一開始，全部的点均为被訪问过
		dis[i] = map[v][i];
	}


	for(i = 1 ; i < n ; ++i){
		int min = inf;
		int pos;

		int j;
		for(j = 1 ; j <= n ; ++j){//寻找眼下的最短路径的最小点
			if(!s[j] && dis[j] < min){
				min = dis[j];
				pos = j;
			}
		}

		s[pos] = 1;

		for(j = 1 ; j <= n ; j++){//遍历u的全部的邻接的边
			if(!s[j] && dis[j] > dis[pos] + map[pos][j]){
				dis[j] = dis[pos] + map[pos][j];//对边进行松弛
			}
		}
	}


	return dis[target];
}



int main(){
	int m;
	while(scanf("%d%d",&n,&m)!=EOF){

		int i;
		int j;
		for(i = 1 ; i <= n ; ++i){
			for(j = 1 ; j <= n ; ++j){
				if(i == j){
					map[i][j] = 0;
				}else{
					map[i][j] = inf;
				}
			}
		}


		for(i = 1 ; i <= m ; ++i){
			int a,b,c;
			scanf("%d%d%d",&a,&b,&c);

			map[a][b] = map[b][a] = c;//这里默认是无向图。。所以要两个方向都做处理,仅仅做一个方向上的处理会WA
		}

		target = n;
		int result = dijkstra(1);

		printf("%d
",result);
	}

	return 0;
}

三、使用bellman-ford算法

bellmen-ford算法介绍：

       思想：事实上bellman-ford的思想和dijkstra的是非常像的，其关键点都在于不断地对边进行松弛。

而最大的差别就在于前者能作用于负边权的情况。事实上现思路还是在求出最短路径后。推断此刻是否还能对便进行松弛，假设还能进行松弛，便说明还有负边权的边

       实现：

bool bellmen_ford(){
	int i;
	for(i = 1 ; i <= n ; ++i){//初始化
		dis[i] = inf;
	}

	dis[source] = 0;//源节点到自己的距离为0

	int j;
	for(i = 1 ; i < n ; ++i){//计算最短路径
		for(j = 1 ; j <= m ; ++j){
			if(dis[edge[j].v] > dis[edge[j].u] + edge[j].weight){
				dis[edge[j].v] = dis[edge[j].u] + edge[j].weight;
			}

			if(dis[edge[j].u] > dis[edge[j].v] + edge[j].weight){
				dis[edge[j].u] = dis[edge[j].v] + edge[j].weight;
			}
		}
	}

	for(j = 1 ; j <= m ; ++j){//推断是否有负边权的边
		if(dis[edge[j].v] > dis[edge[j].u] + edge[j].weight){
			return false;
		}
	}

	return true;
}

基本结构：

struct Edge{
	int u;
	int v;
	int weight;
};

Edge edge[maxm];//用来存储边
int dis[maxn];//dis[i]表示源点到i的距离.一開始是估算距离

 条件：事实上求最短路径的题目的基本条件都是点数、边数、起点、终点

一下给出这一道题的bellman-ford的实现方法

/*
 * NEFU_207_BF.cpp
 *
 *  Created on: 2014年5月28日
 *      Author: Administrator
 */

#include <iostream>
#include <cstdio>

using namespace std;

const int maxn = 105;
const int maxm = 105;

struct Edge{
	int u;
	int v;
	int weight;
};

Edge edge[maxm];//用来存储边
int dis[maxn];//dis[i]表示源点到i的距离.一開始是估算距离

const int inf = 1000000;

int source;
int n,m;

bool bellmen_ford(){
	int i;
	for(i = 1 ; i <= n ; ++i){//初始化
		dis[i] = inf;
	}

	dis[source] = 0;//源节点到自己的距离为0

	int j;
	for(i = 1 ; i < n ; ++i){//计算最短路径
		for(j = 1 ; j <= m ; ++j){
			if(dis[edge[j].v] > dis[edge[j].u] + edge[j].weight){
				dis[edge[j].v] = dis[edge[j].u] + edge[j].weight;
			}

			if(dis[edge[j].u] > dis[edge[j].v] + edge[j].weight){
				dis[edge[j].u] = dis[edge[j].v] + edge[j].weight;
			}
		}
	}

	for(j = 1 ; j <= m ; ++j){//推断是否有负边权的边
		if(dis[edge[j].v] > dis[edge[j].u] + edge[j].weight){
			return false;
		}
	}

	return true;
}

int main(){
	while(scanf("%d%d",&n,&m)!=EOF){
		int i;
		for(i = 1 ; i <= m ; ++i){
			scanf("%d%d%d",&edge[i].u,&edge[i].v,&edge[i].weight);
		}

		source = 1;

		bellmen_ford();

		printf("%d
",dis[n]);
	}

	return 0;
}

四、使用spfa算法来解决。

      思想：用于求单源最短路径，能够适用于负边权的情况。spfa(Shortest Path Faster Algorithm)算法事实上不是什么非常难理解的算法。它仅仅是bellman-ford的队列优化而已。

      模板：

#include <iostream>
#include <cstring>
#include <queue>
using namespace std;

const int N = 105;
const int INF = 99999999;

int map[N][N], dist[N];
bool visit[N];
int n, m;

void init() {//初始化
	int i, j;
	for (i = 1; i < N; i++) {
		for (j = 1; j < N; j++) {
			if (i == j) {
				map[i][j] = 0;
			} else {
				map[i][j] = map[j][i] = INF;
			}
		}
	}
}

/**
 * SPFA算法.
 * 使用spfa算法来求单元最短路径
 * 參数说明:
 * start:起点
 */
void spfa(int start) {
	queue<int> Q;

	int i, now;
	memset(visit, false, sizeof(visit));
	for (i = 1; i <= n; i++){
		dist[i] = INF;
	}

	dist[start] = 0;
	Q.push(start);
	visit[start] = true;
	while (!Q.empty()) {
		now = Q.front();
		Q.pop();
		visit[now] = false;
		for (i = 1; i <= n; i++) {
			if (dist[i] > dist[now] + map[now][i]) {
				dist[i] = dist[now] + map[now][i];
				if (visit[i] == 0) {
					Q.push(i);
					visit[i] = true;
				}
			}
		}
	}
}

这道题的代码例如以下：

/*
 * NEFU207.CPP
 *
 *  Created on: 2015年3月26日
 *      Author: Administrator
 */


#include <iostream>
#include <cstring>
#include <queue>
using namespace std;

const int N = 105;
const int INF = 99999999;

int map[N][N], dist[N];
bool visit[N];
int n, m;

void init() {//初始化
	int i, j;
	for (i = 1; i < N; i++) {
		for (j = 1; j < N; j++) {
			if (i == j) {
				map[i][j] = 0;
			} else {
				map[i][j] = map[j][i] = INF;
			}
		}
	}
}

/**
 * SPFA算法.
 * 使用spfa算法来求单元最短路径
 * 參数说明:
 * start:起点
 */
void spfa(int start) {
	queue<int> Q;

	int i, now;
	memset(visit, false, sizeof(visit));
	for (i = 1; i <= n; i++){
		dist[i] = INF;
	}

	dist[start] = 0;
	Q.push(start);
	visit[start] = true;
	while (!Q.empty()) {
		now = Q.front();
		Q.pop();
		visit[now] = false;
		for (i = 1; i <= n; i++) {
			if (dist[i] > dist[now] + map[now][i]) {
				dist[i] = dist[now] + map[now][i];
				if (visit[i] == 0) {
					Q.push(i);
					visit[i] = true;
				}
			}
		}
	}
}

int main(){
	while(scanf("%d%d",&n,&m)!=EOF){
		init();

		while(m--){
			int a,b,c;
			scanf("%d%d%d",&a,&b,&c);

			if(map[a][b] > c){
				map[a][b] = map[b][a] = c;
			}
		}

		spfa(1);
		printf("%d
",dist[n]);
	}

	return 0;
}

2、NEFU 313 最短路径问题

题目与分析：

       这一道题。抽象一下。还是“求从a到b的最短距离”。相同能够使用floyd和dijkstra来做。

和上面那道题有点不同的地方就是：由序号点(用序号来描写叙述的点)变成了xy点(用坐标系来描写叙述的点)....算法部分该怎么写还是怎么写。。仅仅是

观察一下。题目已经给出点数、边数、起点、终点。

在“最短路径”的对应的题目中。5个基本条件中已经知道了4个，还差边的信息。即map[][]数据的记录不再有题目给出，而是须要自己写一个distance函数来计算一下

1、floyd

/*
 * NEFU_313.cpp
 *
 *  Created on: 2014年5月27日
 *      Author: pc
 */

#include <iostream>
#include <cstdio>
#include <cmath>

using namespace std;

const int maxn = 105;

double map[maxn][maxn];

int n;
const int inf = INT_MAX;
struct Pointt {
	double x;
	double y;
};

double distance1(Pointt p1, Pointt p2) {
	return sqrt((p1.x - p2.x) * (p1.x - p2.x) + (p1.y - p2.y) * (p1.y - p2.y));
}

void initial() {
	int i;
	int j;

	for (i = 1; i <= n; ++i) {
		for (j = 1; j <= n; ++j) {
			if (i == j) {
				map[i][j] = 0;
			} else {
				map[i][j] = inf;
			}
		}
	}
}
void floyd() {
	int i;
	int j;

	int k;
	for (k = 1; k <= n; ++k) {
		for (i = 1; i <= n; ++i) {
			for (j = 1; j <= n; ++j) {
				if (map[i][j] > map[i][k] + map[k][j]) {
					map[i][j] = map[i][k] + map[k][j];
				}
			}
		}
	}
}

int main() {
	while (scanf("%d", &n) != EOF) {
		int i;

		Pointt p[n + 1];

		for (i = 1; i <= n; ++i) {
			scanf("%lf%lf", &p[i].x, &p[i].y);
		}

		int m;
		scanf("%d", &m);

		initial();

		for (i = 1; i <= m; ++i) {
			int a, b;
			scanf("%d%d", &a, &b);

			map[a][b] = map[b][a] = distance1(p[a], p[b]);
		}

		floyd();

		int start, end;
		scanf("%d%d", &start, &end);

		printf("%.2lf
", map[start][end]);

	}

	return 0;
}

2、dijkstra

/*
 * NEFU_313.cpp
 *
 *  Created on: 2014年5月27日
 *      Author: pc
 */


#include <iostream>
#include <cstdio>
#include <cmath>

using namespace std;

const int maxn = 105;
const int inf = INT_MAX;

int s[maxn];
double dis[maxn];
double map[maxn][maxn];

int n;
int target;

struct Pointt{
	double x;
	double y;
};

double distance1(Pointt p1, Pointt p2){
	return sqrt((p1.x - p2.x)*(p1.x - p2.x) + (p1.y - p2.y)*(p1.y - p2.y));
}

double dijkstra(int v){
	int i;
	for(i =1 ; i <= n ; ++i){
		s[i] = 0;
		dis[i] = map[v][i];
	}



	for(i = 1 ; i < n; ++i){
		double min = inf;
		int pos;

		int j;
		for(j = 1 ; j <= n ; ++j){
			if(!s[j] && dis[j] < min){
				min = dis[j];
				pos = j;
			}
		}

		s[pos] = 1;

		for(j = 1 ; j <= n ; ++j){
			if(!s[j] && dis[j] > dis[pos] + map[pos][j]){
				dis[j] = dis[pos] + map[pos][j];
			}
		}
	}
	return  dis[target];
}


void printfMap(){
	int i;
	int j;
	for(i = 1 ; i <= n ; ++i){
		for(j = 1 ; j <= n ; ++j){
			printf("%lf " ,map[i][j]);
		}

		printf("
");
	}
}

int main(){
	while(scanf("%d",&n)!=EOF){
		Pointt p[n+1];

		int i;
		for(i = 1 ; i <= n ; ++i){
			scanf("%lf%lf",&p[i].x,&p[i].y);
		}

		int j;
		for(i = 1 ; i <= n ; ++i){
			for(j = 1 ; j <= n ; ++j){
				if(i == j){
					map[i][j] = 0;
				}else{
					map[i][j] = inf;
				}
			}
		}


		int m;
		scanf("%d",&m);
		for(i = 1 ; i <= m ; ++i){
			int a,b;
			scanf("%d%d",&a,&b);
			map[a][b] = map[b][a] = distance1(p[a],p[b]);
		}

		int start;
		scanf("%d%d",&start,&target);


		double result = dijkstra(start);

		printf("%.2lf
",result);
	}

	return 0;
}

下面是再次做这道题的时候的代码:

/*
 * NEFU_313.cpp
 *
 *  Created on: 2014年9月6日
 *      Author: pc
 */

#include <iostream>
#include <cstdio>
#include <math.h>


using namespace std;

const int maxn = 105;
const int inf = 99999;


int s[maxn];
double dis[maxn];
double map[maxn][maxn];

int n;
int target;

struct Point{
	int x;
	int y;
}p[maxn];

double mydistance(Point a,Point b){

	return sqrt(pow(a.x-b.x,2) + pow(a.y - b.y,2));
}


void initial(){
	int i;
	int j;
	for(i = 1 ; i <= n ; ++i){
		for(j = 1 ; j <= n ; ++j){
			if(i == j){
				map[i][j] = 0;
			}else{
				map[i][j] = inf;
			}
		}
	}
}


double dijkstra(int v){
	int i;
	for(i = 1 ; i <= n ; ++i){
		s[i] = false;
		dis[i] = map[v][i];
	}

	int j;
	for(i = 1 ; i < n ; ++i){
		double min = inf;
		int pos;

		for(j = 1 ; j <= n ; ++j){
			if(!s[j] && min > dis[j]){
				min = dis[j];
				pos = j;
			}
		}

		s[pos] = true;


		for(j = 1 ; j <= n ; ++j){
			if(!s[j] && dis[j] > dis[pos] + map[pos][j]){
				dis[j] = dis[pos] + map[pos][j];
			}
		}
	}

	return dis[target];
}



int main(){
	while(scanf("%d",&n)!=EOF){
		int i;
		for(i = 1 ; i <= n ; ++i){
			scanf("%d%d",&p[i].x,&p[i].y);
		}

		initial();

		int m;
		scanf("%d",&m);
		for(i = 1 ; i <= m ; ++i){
			int a,b;
			scanf("%d%d",&a,&b);

			double c = mydistance(p[a],p[b]);
			if(map[a][b] > c){
				map[a][b] = map[b][a] = c;//注意,这里是无向图,还是得做一下处理才好,否则会WA
			}
		}


	    int v;
	    scanf("%d%d",&v,&target);

	    double result = dijkstra(v);

	    printf("%.2lf
",result);

	}

	return 0;
}

3)spfa算法

/*
 * NEFU313.cpp
 *
 *  Created on: 2015年3月26日
 *      Author: Administrator
 */




#include <iostream>
#include <cstring>
#include <queue>
#include <cmath>


using namespace std;

const int N = 105;
const int INF = 99999999;

struct Point{
	double x;
	double y;
}points[N];

double getDistance(Point p1,Point p2){
	return sqrt((p1.x - p2.x) * (p1.x - p2.x) + (p1.y - p2.y) * (p1.y - p2.y));
}

double map[N][N];
double dist[N];
bool visit[N];
int n, m;

void init() {//初始化
	int i, j;
	for (i = 1; i < N; i++) {
		for (j = 1; j < N; j++) {
			if (i == j) {
				map[i][j] = 0;
			} else {
				map[i][j] = map[j][i] = INF;
			}
		}
	}
}

/**
 * SPFA算法.
 * 使用spfa算法来求单元最短路径
 * 參数说明:
 * start:起点
 */
void spfa(int start) {
	queue<int> Q;

	int i, now;
	memset(visit, false, sizeof(visit));
	for (i = 1; i <= n; i++){
		dist[i] = INF;
	}

	dist[start] = 0;
	Q.push(start);
	visit[start] = true;
	while (!Q.empty()) {
		now = Q.front();
		Q.pop();
		visit[now] = false;
		for (i = 1; i <= n; i++) {
			if (dist[i] > dist[now] + map[now][i]) {
				dist[i] = dist[now] + map[now][i];
				if (visit[i] == 0) {
					Q.push(i);
					visit[i] = true;
				}
			}
		}
	}
}

int main(){
	while(scanf("%d",&n)!=EOF){
		init();

		int i;
		for(i = 1 ; i <= n ; ++i){
			scanf("%lf%lf",&points[i].x,&points[i].y);
		}

		scanf("%d",&m);

		while(m--){
			int a,b;
			scanf("%d%d",&a,&b);

			map[a][b] = map[b][a] = getDistance(points[a],points[b]);
		}

		int start,end;
		scanf("%d%d",&start,&end);

		spfa(start);

		printf("%.2lf
",dist[end]);
	}
}

3、NEFU 208 宫锁珠帘

题目与分析：

这道题抽象一下，还是“求从a到b的最短距离”。。相同能够使用floyd和dijkstra来做。。

这道题与前面的不同的地方在于：两个点之间可能有多条路(我们保存那条最短的就可以)。

另外，还要理解dijkstra和floyd算法中使用到的map[][]矩阵的含义。

map[i][i] = 0.自己到自己的距离为0

map[i][j] = inf .表示两点之间无法连通

下面是分别用dijkstra、floyd、spfa这三种算法来做的代码。须要注意的是这道题顶点序号的范围是0~n-1，而之前做的题目的定点序号范围都是1~n。

1、floyd

/*
 * NEFU_208.cpp
 *
 *  Created on: 2014年5月27日
 *      Author: pc
 */

#include <iostream>
#include <cstdio>
#include <cmath>

using namespace std;

const int maxn = 105;
const int inf = 10005;
//const int inf = INT_MAX; //注意不要轻易使用INT_MAX.假设这里使用了INT_MAX,那么假设2个inf相加的话,那么久整数溢出了...

int n;
int map[maxn][maxn];


void initial(){
	int i;
	int j;
	for(i = 0 ; i < n ; ++i){
		for(j = 0 ; j < n ; ++j){
			if(i == j){
				map[i][j] = 0;
			}else{
				map[i][j] = inf;
			}
		}
	}
}


void floyd(){
	int i;
	int j;

	int k;
	for( k = 0 ; k < n ; ++k){
		for(i = 0 ; i < n ; ++i){
			for(j = 0 ; j < n ; ++j){
				if(map[i][j] > map[i][k] + map[k][j]){
					map[i][j] = map[i][k] + map[k][j];
				}
			}
		}
	}
}

void printfMap(){
	int i;
	int j;
	for(i = 0 ; i < n ; ++i){
		for(j = 0 ; j < n ; ++j){
			printf("%d " ,map[i][j]);
		}

		printf("
");
	}
}

int main(){
	int m;
	while(scanf("%d%d",&n,&m)!=EOF){

		initial();

		int i;
		for(i = 1 ; i <= m ; ++i){
			int a,b,c;
			scanf("%d%d%d",&a,&b,&c);

			if(c < map[a][b]){//用来解决两个点之间可能有多条道路的问题
				map[a][b] = map[b][a] = c;
			}
		}


		floyd();


		int start,end;

		scanf("%d%d",&start,&end);

		if(map[start][end] == inf){
			printf("-1
");
		}else{
			printf("%d
",map[start][end]);
		}
	}

	return 0;
}

2、dijkstra

/*
 * NEFU_208.cpp
 *
 *  Created on: 2014年5月27日
 *      Author: pc
 */


#include <iostream>
#include <cstdio>

using namespace std;

const int maxn = 105;
const int inf = 10005;

int n;

int s[maxn];
int dis[maxn];
int map[maxn][maxn];

int target;

int dijkstra(int v){

	int i;
	for(i = 0 ; i < n ; ++i){
		s[i] = 0;
		dis[i] = map[v][i];
	}

	for(i = 0 ; i < n-1 ; ++i){//这里的意思实际上是将剩下的n-1个点全部放到S集合中
		int min = inf;
		int pos;

		int j;
		for(j = 0 ; j < n ; ++j){//寻找最短路径点
			if(!s[j] && dis[j] < min){
				min = dis[j];
				pos = j;
			}
		}

		s[pos] = 1;

		for(j = 0 ; j < n ; ++j){
			if(!s[j] && dis[j] > dis[pos] + map[pos][j]){
				dis[j] = dis[pos] + map[pos][j];
			}
		}
	}

	return dis[target];
}


int main(){
	int m;
	while(scanf("%d%d",&n,&m)!=EOF){
		int i;
		int j;
		for(i = 0 ; i < n ; ++i){
			for(j = 0 ; j < n ; ++j){
				if(i == j){
					map[i][j] = 0;
				}else{
					map[i][j] = inf;
				}
			}
		}

		for(i = 1 ; i <= m ; ++i){
			int a,b,c;
			scanf("%d%d%d",&a,&b,&c);

			if(map[a][b] > c){
				map[a][b] = map[b][a] = c;
			}
		}

		int start,end;
		scanf("%d%d",&start,&end);

		target = end;
		int result = dijkstra(start);

		if(result == inf){
			printf("-1
");
		}else{
			printf("%d
",result);
		}
	}

	return 0;
}

3、spfa算法

/*
 * NEFU208.cpp
 *
 *  Created on: 2015年3月26日
 *      Author: Administrator
 */
#include <iostream>
#include <cstring>
#include <queue>
using namespace std;

const int N = 105;
const int INF = 99999999;

int map[N][N], dist[N];
bool visit[N];
int n, m;

void init() {//初始化
	int i, j;
	for (i = 0; i < N; i++) {
		for (j = 0; j < N; j++) {
			if (i == j) {
				map[i][j] = 0;
			} else {
				map[i][j] = map[j][i] = INF;
			}
		}
	}
}

/**
 * SPFA算法.
 * 使用spfa算法来求单元最短路径
 * 參数说明:
 * start:起点
 */
void spfa(int start) {
	queue<int> Q;

	int i, now;
	memset(visit, false, sizeof(visit));
	for (i = 0; i < n; i++){
		dist[i] = INF;
	}

	dist[start] = 0;
	Q.push(start);
	visit[start] = true;
	while (!Q.empty()) {
		now = Q.front();
		Q.pop();
		visit[now] = false;
		for (i = 0; i < n; i++) {//须要注意一下的是,这道题顶点的序号是从0開始的,到n-1.之前的题目都是1~n
			if (dist[i] > dist[now] + map[now][i]) {
				dist[i] = dist[now] + map[now][i];
				if (visit[i] == 0) {
					Q.push(i);
					visit[i] = true;
				}
			}
		}
	}
}


int main(){
	while(scanf("%d%d",&n,&m)!=EOF){
		init();

		while(m--){
			int a,b,c;
			scanf("%d%d%d",&a,&b,&c);


			if(map[a][b] > c){
				map[a][b] = map[b][a] = c;
			}
		}

		int start,end;
		scanf("%d%d",&start,&end);


		spfa(start);

		if(dist[end] == INF){
			printf("-1
");
		}else{
			printf("%d
",dist[end]);
		}
	}

	return 0;
}