今天学习了tensorflow构建回归曲线的知识,其中利用了梯度下降法来提高机器学习创建回归曲线的正确率。
在学习中自己按照其写的代码为:
import numpy as np import tensorflow as tf import matplotlib.pyplot as plt #随机生成一千个点 num_points=1000 vectors_set = [] for _ in range(num_points): x1=np.random.normal(0.0,0.55) y1=x1*0.1+0.3+np.random.normal(0.0,0.05) vectors_set.append([x1,y1]) #生成样本 x_d = [v[0] for v in vectors_set] y_d = [v[1] for v in vectors_set] plt.scatter(x_d,y_d,c='b') plt.show()
W = tf.Variable(tf.compat.v1.random_uniform([1],-1,1),name='W') b= tf.Variable(tf.zeros([1]),name='b') y = W*x_d + b #以预估值y和实际值y_d之间误差 loss = tf.reduce_mean(tf.square(y-y_d),name='loss') optimizer =tf.compat.v1.train.GradientDescentOptimizer(0.5) train= optimizer.minimize(loss,name='train') init = tf.compat.v1.global_variables_initializer() with tf.compat.v1.Session() as sess: sess.run(init) print("W=",sess.run(W),"b=",sess.run(b),"loss=",sess.run(loss)) for _ in range(30): sess.run(train) print("W=",sess.run(W),"b=",sess.run(b),"loss=",sess.run(loss)) plt.scatter(x_d,y_d,c='y') plt.plot(x_d,sess.run(W)*x_d+sess.run(b)) plt.show()
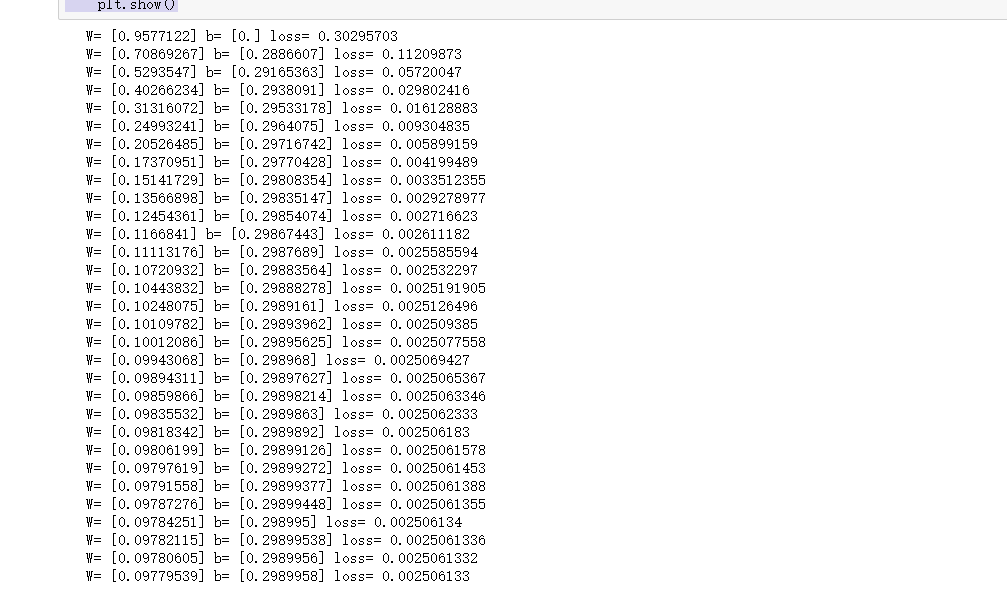
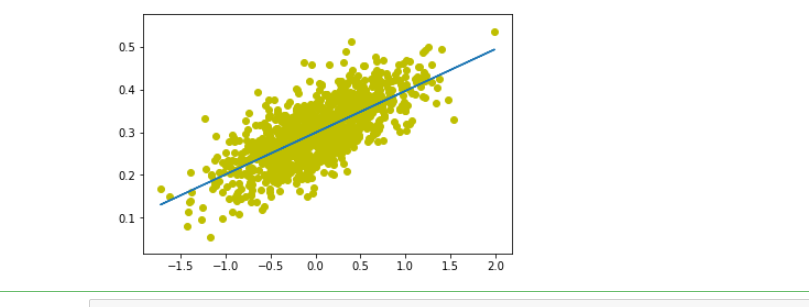
根据案例可以看出,利用梯度下降法可以每次增强构建回归函数的准确度,是比较容易理解上手的方法。