二分查找：
一般而言,对于包含n个元素的列表,用二分查找最多需要log2 n(以2为底，n的对数)步,而简单查找最多需要n步。
仅当列表是有序的时候,二分查找才管用。
函数 binary_search 接受一个有序数组和一个元素。如果指定的元素包含在数组中,这个函数将返回其位置。
low = 0 high = len(list) - 1 mid = (low + high) / 2
guess = list[mid]
如果猜的数字小了,就相应地修改 low 。if guess < item: low = mid + 1
如果猜的数字大了,就修改 high 。if guess > item: high = mid - 1
1 #!coding:utf8 2 3 def binary_select(item, li): 4 low = 0 5 high = len(li) - 1 6 while low <= high: # 0 5, 3 5, 4 5, 5 5 # 所以low==high的情况是比较开头或结尾时 7 mid = int((low+high) / 2) # 2 4 4 8 guess = li[mid] # 5 10 10 # 虽然重复比较了一次，但是索引变了 9 print(mid, guess) 10 if guess == item: 11 return mid 12 elif guess < item: 13 low = mid + 1 14 else: 15 high = mid - 1 16 return None # 没找到的情况 17 18 li = [2, 4, 5, 7, 10, 14] 19 res = binary_select(16, li) 20 print('res: ', res)
运行时间：
最多需要猜测的次数与列表长度相同,这被称为线性时间(linear time)。
二分查找的运行时间为对数时间 (或log时间)。
大O表示法：
仅知道算法需要多长时间才能运行完毕还不够,还需知道运行时间如何随列表增长而增加。它表示为检查长度为n的列表,需要执行log n次操作。大 O 表示法指出了最糟情况下的运行时间。
常见运行时间：
O(log n),也叫对数时间,这样的算法包括二分查找。
O(n),也叫线性时间,这样的算法包括简单查找。
O(n * log n),这样的算法包括第4章将介绍的快速排序——一种速度较快的排序算法。
O(n 2 ),这样的算法包括第2章将介绍的选择排序——一种速度较慢的排序算法。
O(n!),这样的算法包括接下来将介绍的旅行商问题的解决方案——一种非常慢的算法。
旅行商问题：要前往这n个城市,同时要确保旅程最短。运行时间为O(n!)。
数组和链表
数组中的元素需要一整块连续的内存来保存。当需要向数组中添加元素时需要另开辟一整块空间。
链表中的元素可存储在内存的任何地方。链表的每个元素都存储了下一个元素的地址,从而使一系列随机的内存地址串在一起。向链表中添加元素，只要将其放入内存，并将其地址保存到前一个元素即可。
在需要读取链表的最后一个元素时,你不能直接读取,因为你不知道它所处的地址,必须先访问元素#1,从中获取元素#2的地址,再访问元素#2并从中获取元素#3的地址,以此类推，直到访问最后一个元素。需要同时读取所有元素时,链表的效率很高:你读取第一个元素,根据其中的地址再读取第二个元素,以此类推。但如果你需要跳跃,链表的效率真的很低。
数组与此不同:你知道其中每个元素的地址。例如,假设有一个数组,它包含五个元素,起始地址为00,那么元素#5的地址是多少呢?只需执行简单的数学运算就知道:04。需要随机地读取元素时,数组的效率很高,因为可迅速找到数组的任何元素。在链表中,元素并非靠在一起的,你无法迅速计算出第五个元素的内存地址,而必须先访问第一个元素以获取第二个元素的地址,再访问第二个元素以获取第三个元素的地址,以此类推,直到访问第五个元素。
两种访问方式:随机访问和顺序访问。
链表擅长插入和删除,而数组擅长随机访问。
选排：
假设从小到大排序，遍历整个列表找出最大的元素，将该元素添加到一个新列表并从原有列表删除；以此重复这种操作，直到原有列表中的元素都移到新列表中，新列表即为已排序好的结果。
1 #!coding:utf8 2 3 def findSmall(li): 4 smallest = li[0] 5 smallest_index = 0 # 存储最小元素的索引 6 for i in range(1, len(li)): 7 if li[i] < smallest: 8 smallest = li[i] 9 smallest_index = i 10 return smallest_index 11 12 13 def selectionSort(li): 14 newli = [] 15 for i in range(len(li)): 16 smallest = findSmall(li) 17 newli.append(li.pop(smallest)) 18 return newli 19 20 print(selectionSort([5, 3, 6, 2, 10, 4]))
same as this:
1 #!coding:utf8 2 3 def select_num(li): 4 num = 0 5 for i in range(1, len(li)): 6 if li[num] < li[i]: 7 num = i 8 return num 9 10 def select_sort(li): 11 new_li = [] 12 while li: 13 num = select_num(li) 14 new_li.append(li.pop(num)) 15 print('new_list: ', new_li) 16 17 select_sort([5, 3, 6, 2, 10, 4, 2.5])
递归：
递归只是让解决方案更清晰,并没有性能上的优势。实际上,在有些情况下,使用循环的性能更好。Leigh Caldwell在Stack Overflow上说的一句话:“如果使用循环,程序的性能可能更高;如果使用递归,程序可能更容易理解。如何选择要看什么对你来说更重要。
编写递归函数时,必须告诉它何时停止递归。正因为如此,每个递归函数都有两部分:基线条件(base case)和递归条件(recursive case)。递归条件指的是函数调用自己,而基线条件则指的是函数不再调用自己,从而避免形成无限循环。
栈：
一叠便条:插入的待办事项放在清单的最前面;读取待办事项时,你只读取最上面的那个,并将其删除。因此这个待办事项清单只有两种操作:压入(插入)和弹出(删除并读取)。
调用栈：
1 #!coding:utf8 2 3 def greet(name): 4 print("hello, " + name + "!") 5 greet2(name) 6 print("getting ready to say bye...") 7 bye() 8 9 10 def greet2(name): 11 print("how are you, " + name + "?") 12 13 14 def bye(): 15 print("ok bye!") 16 17 greet('maggie')
当调用great('maggie')时，计算机首先为该函数调用分配一块内存，接着打印`hello, maggie！`；在调用greet2('maggie')时，计算机同样为该函数分配一块内存，计算机使用一个栈来表示这些内存块,其中第二个内存块位于第一个内存块上面。当打印完`how are you, maggie?`时，从函数greet2调用返回到greet，此时,栈顶的内存块被弹出；接着打印`getting ready to say bye...`，然后调用函数bye，同样再栈顶添加函数bye的内存块...，像这样，用于存储多个函数的变量的栈，被成为调用栈。
递归调用栈：
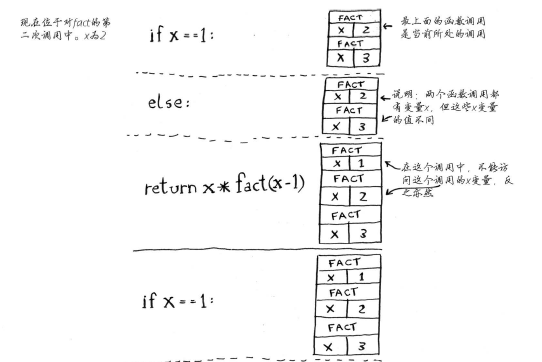1 #!coding:utf8 2 3 def fact(x): 4 if x == 1: 5 return 1 6 else: 7 return x * fact(x-1)
1
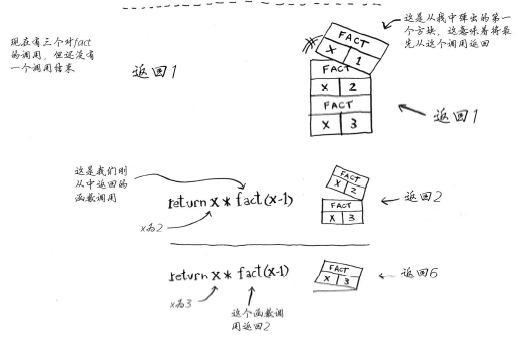1
1
分而治之
假设有一块土地(长宽为640m、1680m)，把其分成均匀的方块(长宽相等)，且方块尽可能大。
使用D&C策略！
D&C算法是递归的。使用D&C解决问题的过程包括两个步骤。
(1) 找出基线条件，这种条件必须尽可能简单。
(2) 不断将问题分解（或者说缩小规模），直到符合基线条件。
首先，找出基线条件。最容易处理的情况是，一条边的长度是另一条边的整数倍。如果一边长25 m，另一边长50 m，那么可使用的最大方块为 25 m×25 m。换言之，可以将这块地分成两个这样的方块。
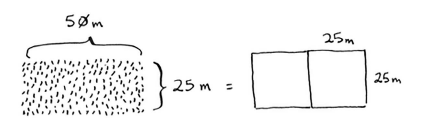
现在需要找出递归条件，这正是D&C的用武之地。根据D&C的定义，每次递归调用都必须缩小问题的规模。如何缩小前述问题的规模呢？我们首先找出这块地可容纳的最大方块。
以此划分。。。直到满足基线条件。
给定一个数字列表，将这些数字相加，最后返回结果。
第一步：找出基线条件。最简单的数组什么样呢？如果数组不包含任何元素或只包含一个元素，计算总和将非常容易。因此这就是基线条件。
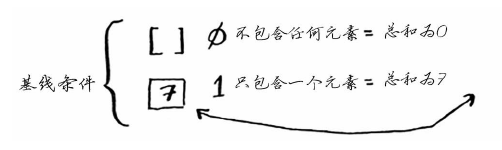
第二步：每次递归调用都必须离空数组更近一步。
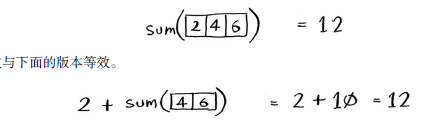
这两个版本的结果都为12，但在第二个版本中，给函数sum传递的数组更短。换言之，这缩小了问题的规模！
1 #!coding:utf8 2 3 def sum_num(li): 4 if len(li) <= 1: # 基线条件 5 return sum(li) 6 else: # 递归条件 7 i = li.pop() 8 return i + sum_num(li) 9 10 print(sum_num([i for i in range(998)]))
快排：
基线条件为数组为空或只包含一个元素。在这种情况下，只需原样返回数组——根本就不用排序。
首先，从数组中选择一个元素，这个元素被称为基准值（pivot）。我们暂时将数组的第一个元素用作基准值。
接下来，找出比基准值小的元素以及比基准值大的元素。这被称为分区（partitioning）。现在你有：
一个由所有小于基准值的数字组成的子数组；
基准值；
一个由所有大于基准值的数组组成的子数组。
分区之后得到的两个子数组是无序的。如果子数组是有序的，就可以像下面这样合并得到一个有序的数组：左边的数组 + 基准值 +右边的数组。
1 def quick_sort(li): 2 if len(li) <= 1: # 基线条件为列表为空或只包含一个元素，这时只需原样返回数组--根本不需要排序。 3 return li 4 elif len(li) == 2: 5 if li[0] > li[1]: 6 li[0], li[1] = li[1], li[0] 7 return li 8 elif len(li) >= 3: 9 # 分区 10 # li1 = li2 = [] # 不能这么写。。 11 li1 = [] 12 li2 = [] 13 pivot = li[0] 14 for i in li[1:]: 15 if i < pivot: 16 li1.append(i) 17 else: 18 li2.append(i) 19 li1 = quick_sort(li1) 20 li2 = quick_sort(li2) 21 22 return li1 + [pivot] + li2
优化之后：
1 #!coding:utf8 2 3 def quick_sort(li): 4 if len(li) <= 1: 5 return li 6 else: 7 pivot = li[0] 8 li1 = quick_sort([i for i in li[1:] if i < pivot]) 9 li2 = quick_sort([i for i in li[1:] if i >= pivot]) 10 return li1 + [pivot] + li2
冒泡排序：
1 #!coding:utf8 2 3 # 冒泡排序 4 # 轮 比较次数 5 # 0 len -1 6 # 1 len - 2 7 # 2 8 # 3 9 # 4 10 # 。。。 11 # i len - i - 1 12 def bubble_sort(li): 13 for i in range(len(li)-1): 14 for j in range(len(li)-i-1): 15 if li[j] < li[j+1]: 16 li[j], li[j+1] = li[j+1], li[j] 17 print(li) 18 19 bubble_sort([5, 3, 7, 2, 1, 0])
散列函数：O(1)
无论给它什么数据，它都还返回一个数字。即`将输入映射到数字`。
散列函数必须满足一些要求。
它必须是一致的。例如，假设你输入apple时得到的是4，那么每次输入apple时，得到的都必须为4。如果不是这样，散列表将毫无用处。
它应将不同的输入映射到不同的数字。例如，如果一个散列函数不管输入是什么都返回1，它就不是好的散列函数。最理想的情况是，将不同的输入映射到不同的数字。
散列表
结合使用散列函数和数组创建了一种被称为散列表（hash table）的数据结构。散列表学习到的第一种包含额外逻辑的数据结构。数组和链表都被直接映射到内存，但散列表更复杂，它使用散列函数来确定元素的存储位置。
散列表也被称为散列映射、映射、字典和关联数组。散列表的速度很快！你可以立即获取数组中的元素，而散列表也使用数组来存储数据，因此其获取元素的速度与数组一样快。
你可能根本不需要自己去实现散列表，任一优秀的语言都提供了散列表实现。Python提供的散列表实现为字典。
散列表的应用：
缓存：缓存是一种常用的加速方式，所有大型网站都使用缓存，而缓存的数据则存储在散列表中！(将页面URL映射到页面数据)
冲突：
假设你有一个数组，它包含26个位置。
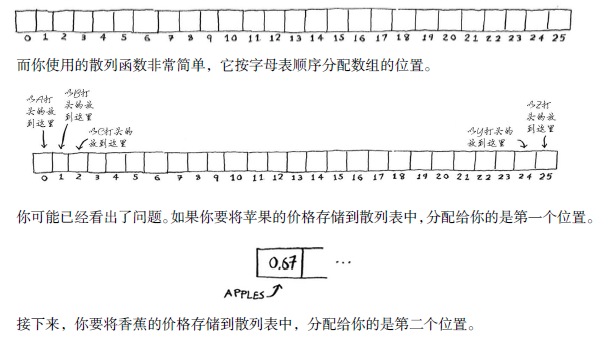
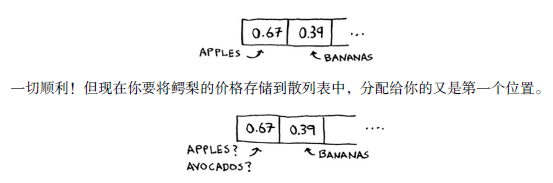
这种情况被称为冲突（collision）：给两个键分配的位置相同。
如果你将鳄梨的价格存储到这个位置，将覆盖苹果的价格，以后再查询苹果的价格时，得到的将是鳄梨的价格！冲突很糟糕，必须要避免。处理冲突的方式很多，最简单的办法如下：如果两个键映射到了同一个位置，就在这个位置存储一个链表。
小结：
散列函数很重要。前面的散列函数将所有的键都映射到一个位置，而最理想的情况是，散列函数将键均匀地映射到散列表的不同位置。
如果散列表存储的链表很长，散列表的速度将急剧下降。然而，如果使用的散列函数很好，这些链表就不会很长！
性能：
在平均情况下，散列表执行各种操作的时间都为O(1)。O(1)被称为常量时间。它并不意味着马上，而是说不管散列表多大，所需的时间都相同。
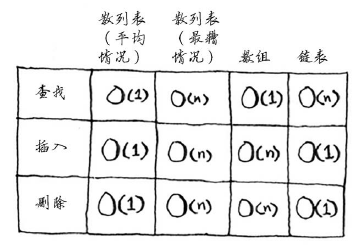
在平均情况下，散列表的查找（获取给定索引处的值）速度与数组一样快，而插入和删除速度与链表一样快，因此它兼具两者的优点！但在最糟情况下，散列表的各种操作的速度都很慢。因此，在使用散列表时，避开最糟情况至关重要。
为此，需要避免冲突。而要避免冲突，需要有：
较低的填装因子；
良好的散列函数。
填装因子：散列表包含的元素数 / 位置总数。
最短路径问题：
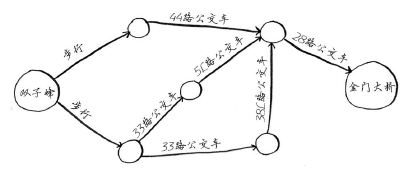
广度优先搜索：解决最短路径问题的算法被称为广度优先搜索。
要确定如何从双子峰前往金门大桥，需要两个步骤。
(1) 使用图来建立问题模型。
(2) 使用广度优先搜索解决问题。
图：模拟一组连接。图由节点和边组成。一个节点可能与众多节点直接相连，这些节点被称为邻居。
广度优先搜索是一种用于图的查找算法，可帮助回答两类问题：
第一类问题，从节点A出发，有前往节点B的路径吗？
第二类问题从节点A出发，前往节点B的哪条路径最短？
如果Alice不是芒果销售商，就将其朋友也加入到名单中。这意味着你将在她的朋友、朋友的朋友等中查找。使用这种算法将搜遍你的整个人际关系网，直到找到芒果销售商。这就是广度优先搜索算法。只有按添加顺序查找时才会达到优先目的。有一个可实现这种目的的数据结构--队列。
队列：
队列是一种先进先出（First In First Out，FIFO）的数据结构，而栈是一种后进先出（Last In First Out，LIFO）的数据结构。
实现图：(通过散列表，即字典)
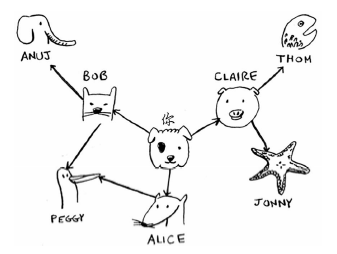
1 graph = {} 2 graph["you"] = ["alice", "bob", "claire"] 3 graph["bob"] = ["anuj", "peggy"] 4 graph["alice"] = ["peggy"] 5 graph["claire"] = ["thom", "jonny"] 6 graph["anuj"] = [] 7 graph["peggy"] = [] 8 graph["thom"] = [] 9 graph["jonny"] = [] 10 print(graph) 11 12 # 结果： 13 {'you': ['alice', 'bob', 'claire'], 'bob': ['anuj', 'peggy'], 'alice': ['peggy'], 'claire': ['thom', 'jonny'], 'anuj': [], 'peggy': [], 'thom': [], 'jonny': []}
Anuj、Peggy、Thom和Jonny都没有邻居，这是因为虽然有指向他们的箭头，但没有从他们出发指向其他人的箭头。这被称为有向图（directed graph），其中的关系是单向的。因此，Anuj是Bob的邻居，但Bob不是Anuj的邻居。无向图（undirected graph）没有箭头，直接相连的节点互为邻居。例如，下面两个图是等价的。
实现算法：
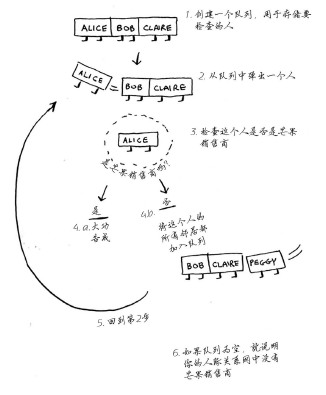
Peggy既是Alice的朋友又是Bob的朋友，因此她将被加入队列两次：一次是在添加Alice的朋友时，另一次是在添加Bob的朋友时。因此，搜索队列将包含两个Peggy。但你只需检查Peggy一次，看她是不是芒果销售商。如果你检查两次，就做了无用功。因此，检查完一个人后，应将其标记为已检查，且不再检查他。如果不这样做，就可能会导致无限循环。
因此，检查一个人之前，要确认之前没检查过他。为此，你可使用一个列表来记录检查过的人。
1 #!coding:utf8 2 from collections import deque 3 4 graph = {} 5 graph["you"] = ["alice", "bob", "claire"] 6 graph["bob"] = ["anuj", "peggy"] 7 graph["alice"] = ["peggy"] 8 graph["claire"] = ["thom", "jonny"] 9 graph["anuj"] = [] 10 graph["peggy"] = [] 11 graph["thom"] = [] 12 graph["jonny"] = [] 13 14 def searcher(graph): 15 search_queue = deque() 16 search_queue += graph['you'] 17 searched = [] 18 19 while search_queue: # 只要队列不为空 20 person = search_queue.popleft() # 就取出其中的第一个人 21 if person in searched: # 如果这个人已经检查过，就跳过检查下一个人 22 continue 23 if person_is_seller(person): # 检查这个人是否是芒果销售商 24 print(person + ' is a mango serler!') # 是芒果销售商 25 return True 26 else: 27 search_queue += graph[person] # 不是芒果销售商。将这个人的朋友都加入搜索队列 28 searched.append(person) # 已检查过的人添加到检查列表 29 return False # 如果到达了这里，就说明队列中没人是芒果销售商 30 31 32 def person_is_seller(name): 33 return name[-1] == 'm' 34 35 searcher(graph)
运行时间：
如果你在你的整个人际关系网中搜索芒果销售商，就意味着你将沿每条边前行（记住，边是从一个人到另一个人的箭头或连接），因此运行时间至少为O(边数)。
你还使用了一个队列，其中包含要检查的每个人。将一个人添加到队列需要的时间是固定的，即为O(1)，因此对每个人都这样做需要的总时间为O(人数)。所以，广度优先搜索的运行时间为O(人数 + 边数)，这通常写作O(V + E)，其中V为顶点（vertice）数，E为边数。
拓扑排序：
如果任务A依赖于任务B，在列表中任务A就必须在任务B后面。这被称为拓扑排序，使用它可根据图创建一个有序列表。
树：
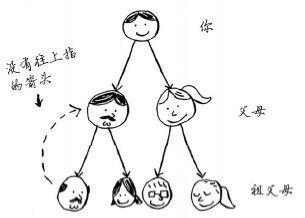
树是一种特殊的图，其中没有往后指的边。
狄克斯特拉算法
最快路径：
狄克斯特拉算法包含4个步骤。
(1) 找出“最便宜”的节点，即可在最短时间内到达的节点。
(2) 更新该节点的邻居的开销，其含义将稍后介绍。
(3) 重复这个过程，直到对图中的每个节点都这样做了。
(4) 计算最终路径。
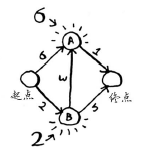
1. 找出最便宜的节点，最便宜的节点为B。
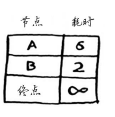
2. 计算(从起点)经节点B前往其(节点B的)各个邻居所需的时间。
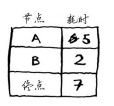
对于节点B的邻居，如果找到前往它的更短路径(直接到节点A需要6分钟，经由节点B到节点A需要5分钟)，就更新其开销。在这里，你找到了：
前往节点A的更短路径（时间从6分钟缩短到5分钟）；
前往终点的更短路径（时间从无穷大缩短到7分钟）。
3. 重复
重复第一步，对节点B来说，便宜节点为A，节点A的邻居为终点。
重复第二步，更新节点A的邻居的开销(从节点B经由节点A到终点的时间比直接到达缩短1分钟)，
现在，你知道：从起点
前往节点B需要2分钟；
前往节点A需要5分钟；
前往终点需要6分钟。
4. 计算最终路径
有关属于：
权重：每条边上的关联数字。
带权重的图称为加权图（weighted graph），不带权重的图称为非加权图（unweighted graph）。
要计算非加权图中的最短路径，可使用广度优先搜索。要计算加权图中的最短路径，可使用狄克斯特拉算法。
图还可能有环，像下面这样：
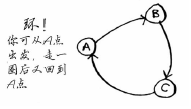
环增加了权重，因此，绕环的路径不可能是最短的路径。
无向图意味着两个节点彼此指向对方，其实就是环！
狄克斯特拉算法只适用于有向无环图。
Rama想拿一本乐谱换架钢琴。
Alex说：“这是我最喜欢的乐队Destroyer的海报，我愿意拿它换你的乐谱。如果你再加5美元，还可拿乐谱换我这张稀有的Rick Astley黑胶唱片。”
Amy说：“哇，我听说这张黑胶唱片里有首非常好听的歌曲，我愿意拿我的吉他或架子鼓换这张海报或黑胶唱片。”
Beethoven惊呼：“我一直想要吉他，我愿意拿我的钢琴换Amy的吉他或架子鼓。”
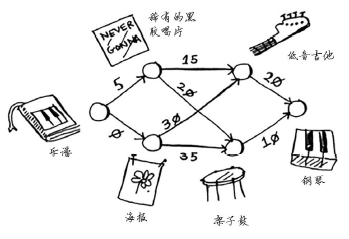
那么问题来了，用乐谱换钢琴，怎么个换法花钱最少。
创建一个表格，列出各个节点的开销，即到达节点需要额外支付多少钱。
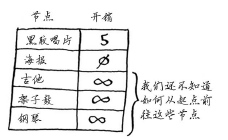
在执行狄克斯特拉算法的过程中，你将不断更新这个表。为计算最终路径，还需在这个表中添加表示父节点的列。
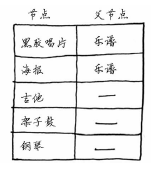
第一步：找出最便宜的节点。在这里，换海报最便宜，不需要支付额外的费用。还有更便宜的换海报的途径吗？这一点非常重要，你一定要想一想。Rama能够通过一系列交换得到海报，还能额外得到钱吗？想清楚后接着往下读。答案是不能，因为海报是Rama能够到达的最便宜的节点，没法再便宜了。
第二步：计算前往该节点的各个邻居的开销。
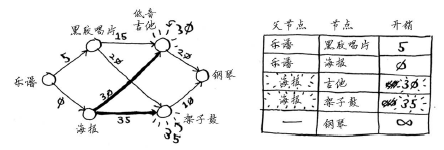
第三步：
再次执行第一步：下一个最便宜的节点是黑胶唱片——需要额外支付5美元。(和之前想的还不一样)
再次执行第二步：更新黑胶唱片的各个邻居的开销。
你更新了架子鼓和吉他的开销！这意味着经“黑胶唱片”前往“架子鼓”和“吉他”的开销更低，因此你将这些乐器的父节点改为黑胶唱片。
下一个最便宜的是吉他，因此更新其邻居的开销。
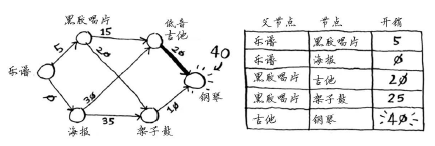
最后，对最后一个节点——架子鼓，做同样的处理。
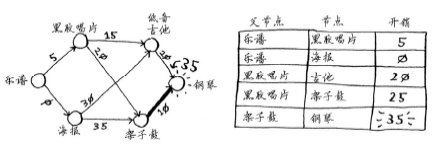
如果用架子鼓换钢琴，Rama需要额外支付的费用更少。因此，采用最便宜的交换路径时，Rama需要额外支付35美元。
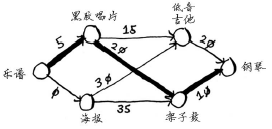
负权边：
假设黑胶唱片不是Alex的，而是Sarah的，且Sarah愿意用黑胶唱片和7美元换海报。换句话说，换得Alex的海报后，Rama用它来换Sarah的黑胶唱片时，不但不用支付额外的费用，还可得7美元。对于这种情况，如何在图中表示出来呢？
从黑胶唱片到海报的边的权重为负！即这种交换让Rama能够得到7美元。现在，Rama有两种
获得海报的方式。
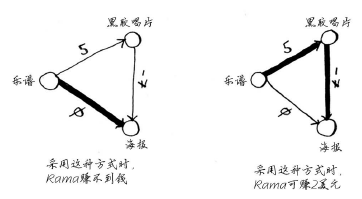
第二种方式更划算——Rama可赚2美元！你可能还记得，Rama可以用海报换架子鼓，但现在
有两种换得架子鼓的方式。
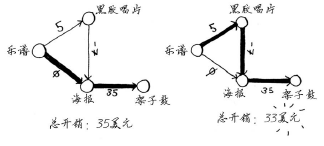
第二种方式的开销少2美元，他应采取这种方式。然而，如果你对这个图运行狄克斯特拉算法，Rama将选择错误的路径——更长的那条路径。如果有负权边，就不能使用狄克斯特拉算法。
实现：
以下面的图为例
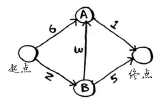
要编写解决这个问题的代码，需要三个散列表。
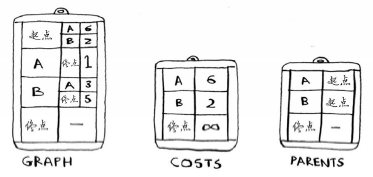
随着算法的进行，你将不断更新散列表costs和parents。
首先，需要实现这个图，可以使用一个散列表。
在前一章中，你像下面这样将节点的所有邻居都存储在散列表中。
graph["you"] = ["alice", "bob", "claire"]
1 #!coding:utf8 2 3 # 权重图，当前节点到邻居节点的映射 4 graph = {} 5 graph["start"] = {} 6 graph["start"]["a"] = 6 7 graph["start"]["b"] = 2 8 9 graph["a"] = {} 10 graph["a"]["fin"] = 1 11 12 graph["b"] = {} 13 graph["b"]["a"] = 3 14 graph["b"]["fin"] = 5 15 16 graph["fin"] = {} 17 18 # print(graph) 19 20 # 开销 21 infinity = float("inf") 22 costs = {} 23 costs["a"] = 6 24 costs["b"] = 2 25 costs["fin"] = infinity 26 # print(costs) 27 # 父节点 28 parents = {} 29 parents["a"] = "start" 30 parents["b"] = "start" 31 parents["fin"] = None 32 33 # 一个数组，记录处理过的节点 34 processed = [] 35 36 def find_lowest_cost_node(costs): 37 lowest_cost = float('inf') 38 lowest_cost_node = None 39 for node in costs: 40 cost = costs[node] 41 if cost < lowest_cost and node not in processed: 42 lowest_cost = cost 43 lowest_cost_node = node 44 return lowest_cost_node 45 46 # 在未处理的节点中找出开销最小的节点，最开始是节点B，然后是节点A，然后是终点，再然后就是空了 47 node = find_lowest_cost_node(costs) 48 while node is not None: 49 cost = costs[node] 50 neighboors = graph[node] 51 for n in neighboors.keys(): # 遍历当前节点的所有邻居 52 new_cost = cost + neighboors[n] 53 if costs[n] > new_cost: # 如果经当前节点前往该邻居更近 54 costs[n] = new_cost # 就更新该邻居的开销 55 parents[n] = node # 同时将该邻居的父节点设置为当前节点 56 processed.append(node) # 将当前节点标记为处理过 57 node = find_lowest_cost_node(costs) # 找出来接下来要处理的节点并循环 58 59 # 路线 60 paths = ['fin'] 61 before = parents['fin'] 62 for n in range(len(parents)-1): 63 paths.insert(0, before) 64 before = parents[before] 65 paths.insert(0, 'start') 66 print(paths) # 路线 67 print(costs['fin']) # 最短距离
7.1实例A图：不是所有节点都要走
1 #!coding:utf8 2 3 # 权重图，当前节点到邻居节点的映射 4 graph = {} 5 graph["start"] = {} 6 graph["start"]["a"] = 5 7 graph["start"]["b"] = 2 8 9 graph["a"] = {} 10 graph["a"]["c"] = 4 11 graph["a"]["d"] = 2 12 13 graph["b"] = {} 14 graph["b"]["a"] = 8 15 graph["b"]["d"] = 7 16 17 graph["c"] = {} 18 graph["c"]["d"] = 6 19 graph["c"]["fin"] = 3 20 21 graph["d"] = {} 22 graph["d"]["fin"] = 1 23 24 graph["fin"] = {} 25 26 # print(graph) 27 28 # 开销 29 infinity = float("inf") 30 costs = {} 31 costs["a"] = 5 32 costs["b"] = 2 33 costs["c"] = infinity 34 costs["d"] = infinity 35 costs["fin"] = infinity 36 # print(costs) 37 # 父节点 38 parents = {} 39 parents["a"] = "start" 40 parents["b"] = "start" 41 parents["c"] = None 42 parents["d"] = None 43 parents["fin"] = None 44 45 # 一个数组，记录处理过的节点 46 processed = [] 47 48 def find_lowest_cost_node(costs): 49 lowest_cost = float('inf') 50 lowest_cost_node = None 51 for node in costs: 52 cost = costs[node] 53 if cost < lowest_cost and node not in processed: 54 lowest_cost = cost 55 lowest_cost_node = node 56 return lowest_cost_node 57 58 # 在未处理的节点中找出开销最小的节点，最开始是节点B，然后是节点A，然后是终点，再然后就是空了 59 node = find_lowest_cost_node(costs) 60 # print(node) 61 while node is not None: 62 cost = costs[node] 63 neighboors = graph[node] 64 for n in neighboors.keys(): # 遍历当前节点的所有邻居 65 new_cost = cost + neighboors[n] 66 if costs[n] > new_cost: # 如果经当前节点前往该邻居更近 67 costs[n] = new_cost # 就更新该邻居的开销 68 parents[n] = node # 同时将该邻居的父节点设置为当前节点 69 # print('==', node, n, costs, cost, parents) 70 processed.append(node) # 将当前节点标记为处理过 71 # print('===', node, processed) # 通过打印这条信息可以发现，到节点`fin`时没有处理 72 node = find_lowest_cost_node(costs) # 找出来接下来要处理的节点并循环 73 74 print(parents) 75 # 路线 76 # paths = ['fin'] 77 # before = parents['fin'] 78 # # for n in range(len(parents)-1): # 对于有未经过的节点不适用 79 # # while parents[before] != 'start': # 这个把起点的子节点丢失了 80 # for n in range(len(parents)-1): 81 # paths.insert(0, before) 82 # before = parents[before] 83 # if before == 'start': 84 # paths.insert(0, before) 85 # break 86 87 k = 'fin' 88 paths = [k] 89 for n in range(len(parents)): 90 before = parents[k] 91 if before == 'start': 92 paths.insert(0, before) 93 break 94 paths.insert(0, before) 95 k = before 96 97 print(paths) # 路线 98 print(costs['fin']) # 最短距离 99 100 101 # == b a {'a': 5, 'b': 2, 'c': inf, 'd': inf, 'fin': inf} 2 {'a': 'start', 'b': 'start', 'c': None, 'd': None, 'fin': None} 102 # == b d {'a': 5, 'b': 2, 'c': inf, 'd': 9, 'fin': inf} 2 {'a': 'start', 'b': 'start', 'c': None, 'd': 'b', 'fin': None} # 到节点D还有更近的，但这一步只更新到这里 103 # == a c {'a': 5, 'b': 2, 'c': 9, 'd': 9, 'fin': inf} 5 {'a': 'start', 'b': 'start', 'c': 'a', 'd': 'b', 'fin': None} 104 # == a d {'a': 5, 'b': 2, 'c': 9, 'd': 7, 'fin': inf} 5 {'a': 'start', 'b': 'start', 'c': 'a', 'd': 'a', 'fin': None} # 又更新了节点D 105 # == d fin {'a': 5, 'b': 2, 'c': 9, 'd': 7, 'fin': 8} 7 {'a': 'start', 'b': 'start', 'c': 'a', 'd': 'a', 'fin': 'd'} # 接下来是`fin`，但是`fin`没有邻居 106 # == c d {'a': 5, 'b': 2, 'c': 9, 'd': 7, 'fin': 8} 9 {'a': 'start', 'b': 'start', 'c': 'a', 'd': 'a', 'fin': 'd'} 107 # == c fin {'a': 5, 'b': 2, 'c': 9, 'd': 7, 'fin': 8} 9 {'a': 'start', 'b': 'start', 'c': 'a', 'd': 'a', 'fin': 'd'}
7.1实例B：有环
1 # == a c {'a': 10, 'b': inf, 'c': 30, 'fin': inf} 10 {'a': 'start', 'b': None, 'c': 'a', 'fin': None} 2 # == c b {'a': 10, 'b': 31, 'c': 30, 'fin': inf} 30 {'a': 'start', 'b': 'c', 'c': 'a', 'fin': None} 3 # == c fin {'a': 10, 'b': 31, 'c': 30, 'fin': 60} 30 {'a': 'start', 'b': 'c', 'c': 'a', 'fin': 'c'} 4 # == b a {'a': 10, 'b': 31, 'c': 30, 'fin': 60} 31 {'a': 'start', 'b': 'c', 'c': 'a', 'fin': 'c'} # 有换也能处理，环不更新花销
7.1实例C：有负数(也有环)
1 # == a b {'a': 2, 'b': 2, 'c': inf, 'fin': inf} 2 {'a': 'start', 'b': 'start', 'c': None, 'fin': None} # 节点A和节点B花销相等 2 # == b c {'a': 2, 'b': 2, 'c': 4, 'fin': inf} 2 {'a': 'start', 'b': 'start', 'c': 'b', 'fin': None} 3 # == b fin {'a': 2, 'b': 2, 'c': 4, 'fin': 4} 2 {'a': 'start', 'b': 'start', 'c': 'b', 'fin': 'b'} 4 # == c a {'a': 2, 'b': 2, 'c': 4, 'fin': 4} 4 {'a': 'start', 'b': 'start', 'c': 'b', 'fin': 'b'} # 带有`-1`的环负数没有起到作用，节点A的父节点仍然是起点 5 # == c fin {'a': 2, 'b': 2, 'c': 4, 'fin': 4} 4 {'a': 'start', 'b': 'start', 'c': 'b', 'fin': 'b'}
贪婪算法：
教室调度问题：
假设有如下课程表，你希望将尽可能多的课程安排在某间教室上。
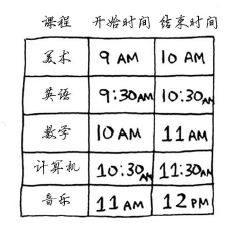
具体做法如下。
(1) 选出结束最早的课，它就是要在这间教室上的第一堂课。
(2) 接下来，选择第一堂课结束后才开始，并且结束最早的课，这将是要在这间教室上的第二堂课。
重复这样做就能找出答案！
贪婪算法的思想：每步都选择局部最优解，最终得到的就是全局最优解。
背包问题：
假设你是个贪婪的小偷，背着可装35磅（1磅≈0.45千克）重东西的背包，在商场伺机盗窃各种可装入背包的商品。你力图往背包中装入价值最高的商品，例如，你可盗窃的商品有下面三种。
根据贪婪算法的原则，音响最贵，应该拿音响，但是之后就没有空间装其他东西了，如果拿电脑和吉他反而价值更高。
在这里，贪婪策略显然不能获得最优解，但非常接近。不过小偷去购物中心行窃时，不会强求所偷东西的总价最高，只要差不多就行了。
从这个示例你得到了如下启示：在有些情况下，完美是优秀的敌人。有时候，你只需找到一个能够大致解决问题的算法，此时贪婪算法正好可派上用场，因为它们实现起来很容易，得到的
结果又与正确结果相当接近。
练习中的问题：
(1). 你在一家家具公司工作，需要将家具发往全国各地，为此你需要将箱子装上卡车。每个箱子的尺寸各不相同，你需要尽可能利用每辆卡车的空间，为此你将如何选择要装上卡车的箱子呢？
(2). 你要去欧洲旅行，总行程为7天。对于每个旅游胜地，你都给它分配一个价值——表示你有多想去那里看看，并估算出需要多长时间。你如何将这次旅行的价值最大化？这显然不是狄克特拉斯算法。
集合覆盖问题：
假设你办了个广播节目，要让全美50个州的听众都收听得到。为此，你需要决定在哪些广播台播出。在每个广播台播出都需要支付费用，因此你力图在尽可能少的广播台播出。现有广播台名单如下。
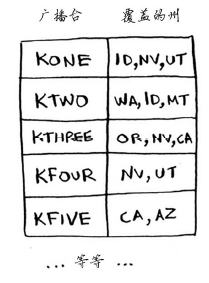
每个广播台都覆盖特定的区域，不同广播台的覆盖区域可能重叠。
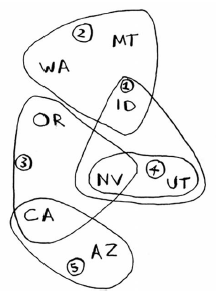
具体方法如下。
(1) 列出每个可能的广播台集合，这被称为幂集（power set）。可能的子集有2n个。
(2) 在这些集合中，选出覆盖全美50个州的最小集合。
问题是计算每个可能的广播台子集需要很长时间。由于可能的集合有2的n次方个，因此运行时间为O(2的n次方)。
使用下面的贪婪算法可得到非常接近的解。
(1) 选出这样一个广播台，即它覆盖了最多的未覆盖州。即便这个广播台覆盖了一些已覆盖的州，也没有关系。
(2) 重复第一步，直到覆盖了所有的州。
在这个例子中，贪婪算法的运行时间为O(n的2次方)，其中n为广播台数量。
1 #!coding:utf8 2 3 # 首先，创建一个列表，其中包含要覆盖的州。 4 states_needed = set(["mt", "wa", "or", "id", "nv", "ut", "ca", "az"]) 5 6 # 可供选择的广播台清单 7 stations = {} 8 stations["kone"] = set(["id", "nv", "ut"]) 9 stations["ktwo"] = set(["wa", "id", "mt"]) 10 stations["kthree"] = set(["or", "nv", "ca"]) 11 stations["kfour"] = set(["nv", "ut"]) 12 stations["kfive"] = set(["ca", "az"]) 13 14 # 使用一个集合来存储最终选择的广播台。 15 final_stations = set() 16 17 # 不断地循环，直到states_needed为空。 18 while states_needed: 19 # 遍历所有的广播台，从中选择覆盖了最多的未覆盖州的广播台。将这个广播台存储在best_station中。 20 best_station = None 21 states_covered = set() # 包含该广播台覆盖的所有未覆盖的州 22 for station, states_for_station in stations.items(): 23 covered = states_needed & states_for_station # 表示当前广播台覆盖的还未覆盖的周 24 if len(covered) > len(states_covered): 25 best_station = station 26 states_covered = covered 27 print('==', best_station) 28 final_stations.add(best_station) # 将best_station添加到最终的广播台列表中。 29 states_needed -= states_covered # 由于该广播台覆盖了一些州，因此不用再覆盖这些州。 30 31 print(final_stations)
NP完全问题：
回看旅行商问题：
阶乘
方法：随便选择出发城市，然后每次选择要去的下一个城市时，都选择还没去的最近的城市。假设旅行商从马林出发。
旅行商问题和集合覆盖问题有一些共同之处：你需要计算所有的解，并从中选出最小/最短的那个。这两个问题都属于NP完全问题。
NP问题的识别：
Jonah正为其虚构的橄榄球队挑选队员。他列了一个清单，指出了对球队的要求：优秀的四分卫，优秀的跑卫，擅长雨中作战，以及能承受压力等。他有一个候选球员名单，其中每个球员都满足某些要求。
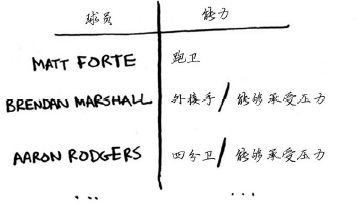
Jonah需要组建一个满足所有这些要求的球队，可名额有限。
规律吧：
元素较少时算法的运行速度非常快，但随着元素数量的增加，速度会变得非常慢。
涉及“所有组合”的问题通常是NP完全问题。
不能将问题分成小问题，必须考虑各种可能的情况。这可能是NP完全问题。
如果问题涉及序列（如旅行商问题中的城市序列）且难以解决，它可能就是NP完全问题。
如果问题涉及集合（如广播台集合）且难以解决，它可能就是NP完全问题。
如果问题可转换为集合覆盖问题或旅行商问题，那它肯定是NP完全问题。
P类问题和NP类问题：
P类问题是指可以在多项式时间复杂度内解决的问题。NP类问题是指可以在多项式时间复杂度内验证的问题。因为可解决的问题一定可验证，因此所有P类问题都是NP类问题，但是，可验证的问题不一定可解决，如果用集合表示的话就是集合P属于集合NP，但是集合NP是否也属于集合P还未解决，更进一步说P是否等于NP还未解决，即`P=NP?`，作为千禧年七大数学难题之一的问题，值100万美元呢，解决了它就能娶你喜欢的人了。
动态规划
即使贪婪算法也无法解决背包问题。
动态规划，一种解决棘手问题的方法，将问题分解成小问题，并着手解决这些小问题。
解决背包问题：
简单算法：尝试各种可能的商品组合，并找出价值最高的组合。时间复杂度为O(2的n次方)，所以行不通。
动态规划：先解决小问题，再逐步解决大问题。
每个动态规划算法都从一个网格开始，背包问题的网格如下。
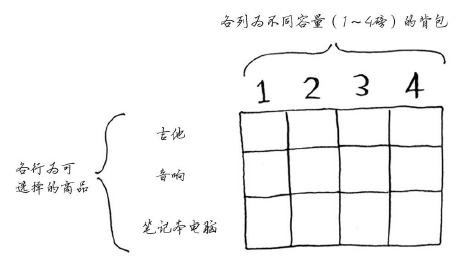
向空单元格里填数，填满时问题就解决了。在每一行，可填的商品都为当前行的商品以及之前各行的商品。
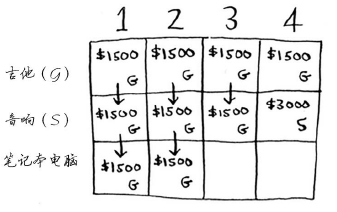
填第3个歌时就需要用到公式了：
填完之后的样子：
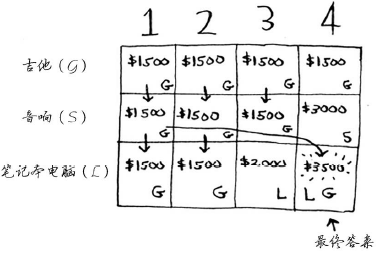
最终答案就是笔记本和吉他。
背包问题FAQ
(1). 再增加一件商品将如何呢
此时需要重新执行前面所做的计算，只需要简单地在后面加上一行即可。
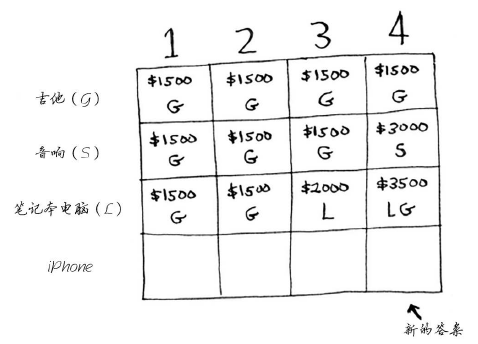
最终结果：
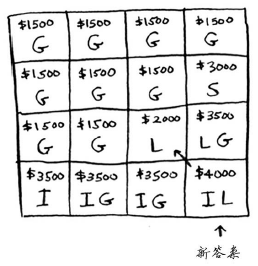
(2). 行的排列顺序发生变化时结果将如何
结果不变
(3). 可以逐列而不是逐行填充网格吗?
就这个问题而言，这没有任何影响，但对于其他问题，可能有影响。
(4). 增加一件更小的商品将如何呢? 假设你还可以偷一条项链，它重0.5磅，价值1000美元。
由于项链的加入，你需要考虑的粒度更细，因此必须调整网格。
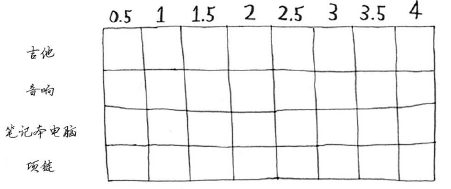
(5). 可以偷商品的一部分吗?
使用动态规划时不行。但是可以使用贪婪算法。首先，尽可能多地拿价值最高的商品；如果拿光了，再尽可能多地拿价值次高的商品，以此类推。
(6). 旅游行程最优化
假设你要去伦敦度假，假期两天，但你想去游览的地方很多。你没法前往每个地方游览，因此你列个单子。
这也是一个背包问题！但约束条件不是背包的容量，而是有限的时间；不是决定该装入哪些商品，而是决定该去游览哪些名胜。(在时间尽量少的情况下，评分最高)
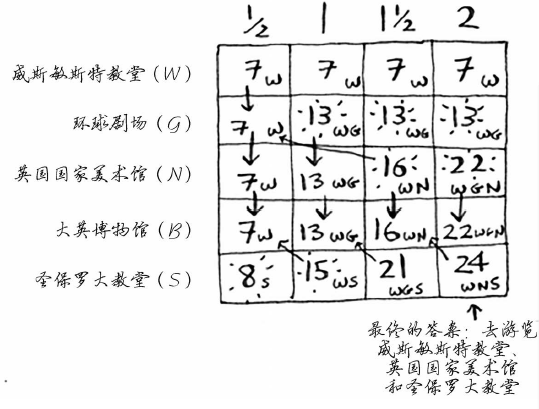剩余的部分找的是上一行，因为不可重复拿。
(7). 处理相互依赖的情况
假设你还想去巴黎，因此在前述清单中又添加了几项。
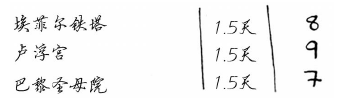其中从伦敦到巴黎需要0.5天时间，已经包含在每项中。到达巴黎后，每个地方都只需1天时间。因此玩这3个地方需要的总时间为3.5天。
因为仅当每个子问题都是离散的，即不依赖于其他子问题时，动态规划才管用。这意味着使用动态规划算法解决不了去巴黎玩的问题。
(8). 计算最终的解时会涉及两个以上的子背包吗?
根据动态规划算法的设计，最多只需合并两个子背包，即根本不会涉及两个以上的子背包。不过这些子背包可能又包含子背包。
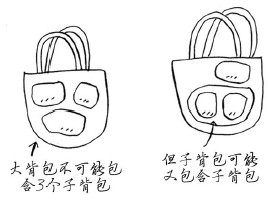
(9). 最优解可能导致背包没装满吗?
完全可能。假设你还可以偷一颗钻石。这颗钻石非常大，重达3.5磅，价值100万美元，比其他商品都值钱得多。你绝对应该把它给偷了！但当你这样做时，余下的容量只有0.5磅，别的什么都装不下。
最长公共子串
通过前面的动态规划问题，你得到了哪些启示呢？
动态规划可帮助你在给定约束条件下找到最优解。在背包问题中，你必须在背包容量给定的情况下，偷到价值最高的商品。
在问题可分解为彼此独立且离散的子问题时，就可使用动态规划来解决。
要设计出动态规划解决方案可能很难。下面是一些通用的小贴士。
每种动态规划解决方案都涉及网格。
单元格中的值通常就是你要优化的值。在前面的背包问题中，单元格的值为商品的价值。
每个单元格都是一个子问题，因此你应考虑如何将问题分成子问题，这有助于你找出网格的坐标轴。
假设你管理着网站dictionary.com。用户在该网站输入单词时，你需要给出其定义。但如果用户拼错了，你必须猜测他原本要输入的是什么单词。例如，Alex想查单词fish，但不小心输入了hish。在你的字典中，根本就没有这样的单词，但有几个类似的单词。在这个例子中，只有两个类似的单词，真是太小儿科了。实际上，类似的单词很可能有数千个。Alex输入了hish，那他原本要输入的是fish还是vista呢？
第一步，绘制表格
用于解决这个问题的网格是什么样的呢？要确定这一点，你得回答如下问题。
单元格中的值是什么？
如何将这个问题划分为子问题？
网格的坐标轴是什么？
在动态规划中，你要将某个指标最大化(比如背包问题中就是价值要求最大；旅程最优化问题中就是评分要求最大)。
在这个例子中，你要找出两个单词的最长公共子串。hish和fish都包含的最长子串是什么呢？hish和vista呢？这就是你要计算的值。
单元格中的值通常就是你要优化的值。在这个例子中，这很可能是一个数字：两个字符串都包含的最长子串的长度。
如何将这个问题划分为子问题呢？你可能需要比较子串：不是比较hish和fish，而是先比较his和fis。每个单元格都将包含这两个子串的最长公共子串的长度。这也给你提供了线索，让你觉得坐标轴很可能是这两个单词。因此，网格可能类似于下面这样。
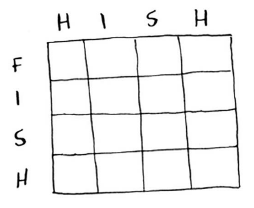
第二步，填充表格
现在，你很清楚网格应是什么样的。填充该网格的每个单元格时，该使用什么样的公式呢？由于你已经知道答案——hish和fish的最长公共子串为ish，因此可以作点弊。
实际上，根本没有找出计算公式的简单办法，你必须通过尝试才能找出管用的公式。有些算法并非精确的解决步骤，而只是帮助你理清思路的框架。
请尝试为这个问题找到计算单元格的公式。给你一点提示吧：下面是这个单元格的一部分。
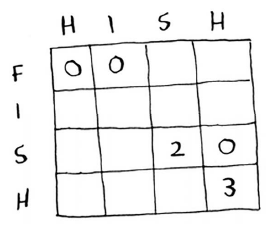
其他单元格的值呢？别忘了，每个单元格都是一个子问题的值。为何单元格(3, 3)的值为2呢？又为何单元格(3, 4)的值为0呢？
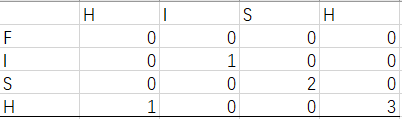
想法是(1, 1)对应的是两个单词的子句`F`和`H`，(1, 2)对应的子句为`F`和`HI`，得出来的答案一致，但是不好落实到代码上。。。这是个问题啊！！
答案揭晓，mmp...
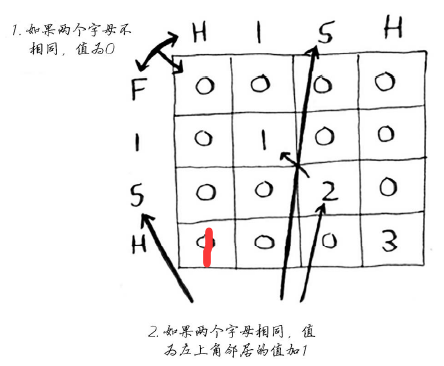
查找单词hish和vista的最长公共子串时，网格如下。
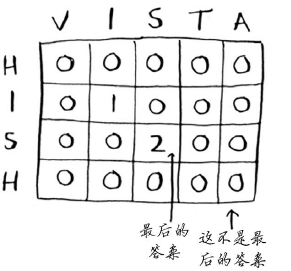
对于前面的背包问题，最终答案总是在最后的单元格中。但对于最长公共子串问题，答案为网格中最大的数字——它可能并不位于最后的单元格中。
我们回到最初的问题：哪个单词与hish更像？hish和fish的最长公共子串包含三个字母，而hish和vista的最长公共子串包含两个字母。因此Alex很可能原本要输入的是fish。
最长公共子序列：
假设Alex不小心输入了fosh，他原本想输入的是fish还是fort呢？
伪代码如下：
最长公共子序列的应用：
生物学家根据最长公共序列来确定DNA链的相似性，进而判断度两种动物或疾病有多相似。最长公共序列还被用来寻找多发性硬化症治疗方案。
你使用过诸如git diff等命令吗？它们指出两个文件的差异，也是使用动态规划实现的。
前面讨论了字符串的相似程度。编辑距离（levenshtein distance）指出了两个字符串的相似程度，也是使用动态规划计算得到的。编辑距离算法的用途很多，从拼写检查到判断用户上传的资料是否是盗版，都在其中。
你使用过诸如Microsoft Word等具有断字功能的应用程序吗？它们如何确定在什么地方断字以确保行长一致呢？使用动态规划！
K最近邻算法：
如果判断这个水果是橙子还是柚子呢？一种办法是看它的邻居。来看看离它最近的三个邻居。
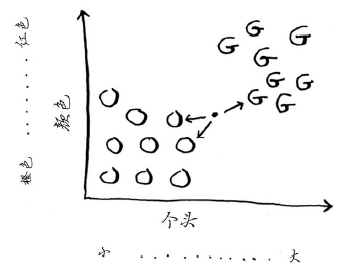
在这三个邻居中，橙子比柚子多，因此这个水果很可能是橙子。祝贺你，你刚才就是使用K最近邻（k-nearest neighbours，KNN）算法进行了分类！
创建推荐系统：
假设你是Netflix，要为用户创建一个电影推荐系统。从本质上说，这类似于前面的水果问题！你可以将所有用户都放入一个图表中。这些用户在图表中的位置取决于其喜好，因此喜好相似的用户距离较近。假设你要向Priyanka推荐电影，可以找出五位与他最接近的用户。假设在对电影的喜好方面，Justin、JC、Joey、Lance和Chris都与Priyanka差不多，因此他们喜欢的电影很可能Priyanka也喜欢！
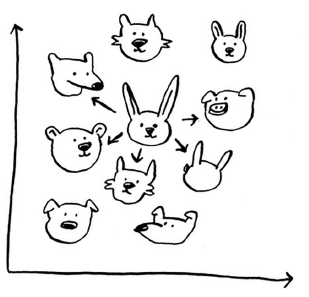
有了这样的图表以后，创建推荐系统就将易如反掌：只要是Justin喜欢的电影，就将其推荐给Priyanka。但还有一个重要的问题没有解决。在前面的图表中，相似的用户相距较近，但如何确定两位用户的相似程度呢？
特征提取
在前面的水果示例中，你根据个头和颜色来比较水果，换言之，你比较的特征是个头和颜色。现在假设有三个水果，你可抽取它们的特征。
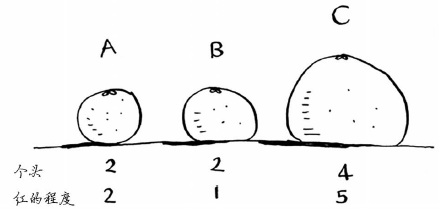
再根据这些特征绘图。
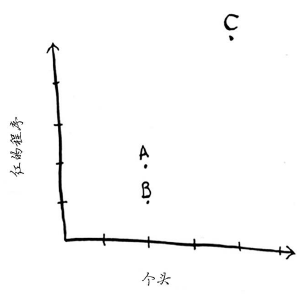
从上图可知，水果A和B比较像。
下面来度量它们有多像。要计算两点的距离，可使用毕达哥拉斯公式(只有两个参数时就是勾股定理)。
距离，
这个距离公式印证了你的直觉：A和B很像。
在推荐系统中，就需要以某种方式将所有用户放到图中。因此，你需要将每位用户都转换为一组坐标，就像前面对水果所做的那样。这样就可以计算用户之间的距离了。
下面是一种将用户转换为一组数字的方式。用户注册时，要求他们指出对各种电影的喜欢程度。这样，对于每位用户，都将获得一组数字！
Priyanka和Justin都喜欢爱情片且都讨厌恐怖片。Morpheus喜欢动作片，但讨厌爱情片（他讨厌好好的动作电影毁于浪漫的桥段）。前面判断水果是橙子还是柚子时，每种水果都用2个数字表
示，在这里，每位用户都用5个数字表示。经计算，Priyanka和Justin的距离的距离为2，Priyanka和Morpheus的距离为24，上述距离表明，Priyanka的喜好更接近于Justin而不是Morpheus。现在要向Priyanka推荐电影将易如反掌：只要是Justin喜欢的电影，就将其推荐给Priyanka，反之亦然。你这就创建了一个电影推荐系统！
如果你是Netflix用户，Netflix将不断提醒你：多给电影评分吧，你评论的电影越多，给你的推荐就越准确。现在你明白了其中的原因：你评论的电影越多，Netflix就越能准确地判断出你与哪些用户类似。
练习
10.1 在Netflix示例中，你使用距离公式计算两位用户的距离，但给电影打分时，每位用户标准并不都相同。假设你有两位用户——Yogi和Pinky，他们欣赏电影的品味相同，但Yogi给喜欢的电影都打5分，而Pinky更挑剔，只给特别好的电影打5分。他们的品味一致，但根据距离算法，他们并非邻居。如何将这种评分方式的差异考虑进来呢？
10.2 假设Netflix指定了一组意见领袖。例如，Quentin Tarantino和Wes Anderson就是Netflix的意见领袖，因此他们的评分比普通用户更重要。请问你该如何修改推荐系统，使其偏重于意见领袖的评分呢？
回归
假设你不仅要向Priyanka推荐电影，还要预测她将给这部电影打多少分。
假设你在伯克利开个小小的面包店，每天都做新鲜面包，需要根据如下一组特征预测当天该烤多少条面包：
天气指数1～5（1表示天气很糟，5表示天气非常好）；
是不是周末或节假日（周末或节假日为1，否则为0）；
有没有活动（1表示有，0表示没有）。
你还有一些历史数据，记录了在各种不同的日子里售出的面包数量。
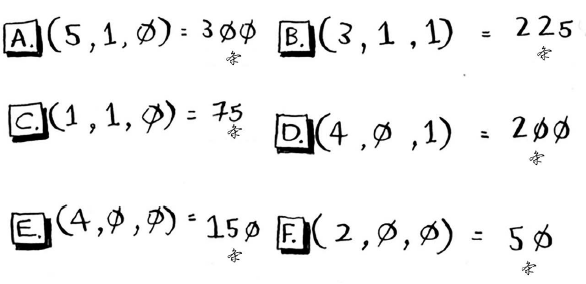
今天是周末，天气不错(坐标为(4, 1, 0))。根据这些数据，预测你今天能售出多少条面包呢？
设置K为4，距离如下，因此最近的邻居为A、B、D和E。
将这些天售出的面包数平均，结果为218.75。这就是你今天要烤的面包数！
余弦相似度：
前面计算两位用户的距离时，使用的都是距离公式。但在实际工作中，经常使用余弦相似度（cosine similarity）。假设有两位品味类似的用户，但其中一位打分时更保守。他们都很喜欢Manmohan Desai的电影Amar Akbar Anthony，但Paul给了5星，而Rowan只给4星。如果你使用距离公式，这两位用户可能不是邻居，虽然他们的品味非常接近。余弦相似度不计算两个矢量的距离，而比较它们的角度，因此更适合处理前面所说的情况。本书不讨论余弦相似度，但如果你要使用KNN，就一定要研究研究它！
通过计算两个向量的夹角余弦值来评估它们的相似度。余弦相似度将向量根据坐标值绘制到向量空间中，如常见的二维空间。
计算方法，
挑选合适的特征
所谓合适的特征，就是：
与要推荐的电影紧密相关的特征；
不偏不倚的特征（例如，如果只让用户给喜剧片打分，就无法判断他们是否喜欢动作片）。
在挑选合适的特征方面，没有放之四海皆准的法则，你必须考虑到各种需要考虑的因素。。。
机器学习简介
OCR
OCR指的是光学字符识别（optical character recognition），这意味着你可拍摄印刷页面的照片，计算机将自动识别出其中的文字。Google使用OCR来实现图书数字化。
OCR是如何工作的呢？我们来看一个例子。请看下面的数字。
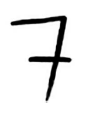
如何自动识别出这个数字是什么呢？可使用KNN。
(1) 浏览大量的数字图像，将这些数字的特征提取出来。
(2) 遇到新图像时，你提取该图像的特征，再找出它最近的邻居都是谁！
这与前面判断水果是橙子还是柚子时一样。一般而言，OCR算法提取线段、点和曲线等特征。
遇到新字符时，可从中提取同样的特征。
与前面的水果示例相比，OCR中的特征提取要复杂得多，但再复杂的技术也是基于KNN等简单理念的。这些理念也可用于语音识别和人脸识别。你将照片上传到Facebook时，它有时候能够自动标出照片中的人物，这是机器学习在发挥作用！
OCR的第一步是查看大量的数字图像并提取特征，这被称为训练（training）。大多数机器学习算法都包含训练的步骤：要让计算机完成任务，必须先训练它。下一个示例是垃圾邮件过滤器，其中也包含训练的步骤。
垃圾邮件过滤器：
垃圾邮件过滤器使用一种简单算法——朴素贝叶斯分类器（Naive Bayes classifier）... 太过简单，跟没说一样mmp...
预测股票市场:
在根据以往的数据来预测未来方面，没有万无一失的方法。未来很难预测，由于涉及的变数太多，这几乎是不可能完成的任务。我尼玛。。。