监督学习(supervised learning)
假设我们有一个数据集(dataset),给出居住面积和房价的关系如下:
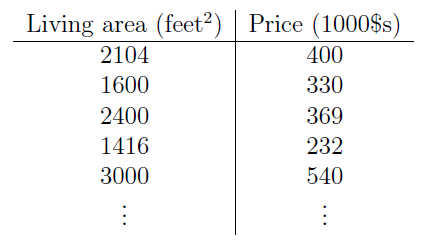
我们以居住面积为横坐标,房价为纵坐标,组成数据点,如(2104, 400),并把这些数据点描到坐标系中,如下:
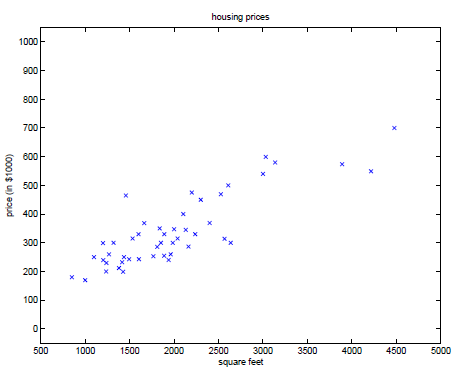
由这些数据,我们怎么才能预测(predict)其他房价呢?其中房价作为居住面积的函数。
为了方便描述,我们用x(i)表示输入变量(即居住面积),也叫做输入特征(features);同时,用y(i)表示输出(即房价),也叫做目标(target)变量。有序对 (x(i), y(i))叫做一个训练样本点(training example);我们用来学习(learn)的数据集,包含m个样本点,也叫做训练集(training set),表示为{(x(i), y(i)); i=1,...,m}。其中上标(i)表示样本点在训练集中的索引,跟指数没关系。另外,我们用X表示输入变量的取值空间,Y表示输出的取值空间,在本文中,X=Y=R。
我们的目的就是学习出一个函数h: X->Y,使得h(x)能够很好的预测y,即|h(x)-y|越小越好。由于历史原因,函数h也叫做假设(hypothesis)。整个流程形象化描述下:
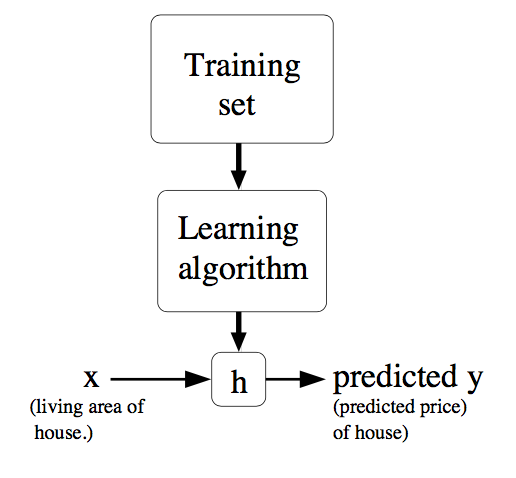
当我们想要预测的目标变量是连续的(continuous),这种学习问题被称之为回归(regression);而离散(discrete)时,则叫做分类(classification)。
线性回归(linear regression)
为了让上面的问题更加一般化,假设我们除了居住面积和房价,还知道房间个数,如下:
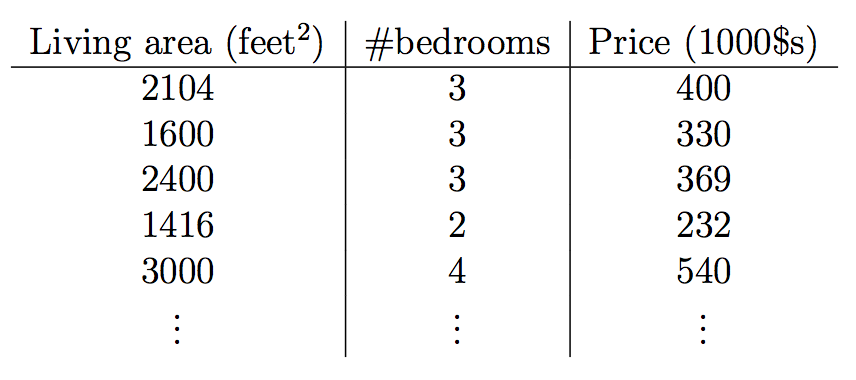
这样,x就是2维空间R2中的向量。x1(i)表示训练集中第i个房子的居住面积,而x2(i)就是它的房间个数。
学习之前,我们需要先决定函数h的表达式。最原始的想法就是,用x的线性函数来拟合(approximate)y。如下:
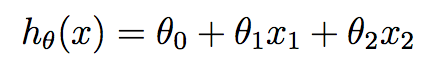
其中,θi 是参数,也叫权值(weight)。在不会引起误解的情况下,我们通常把hθ(x)中的下标θ去掉,简单表示为h(x)。进一步地,我们令x0=1(即截距),使得:
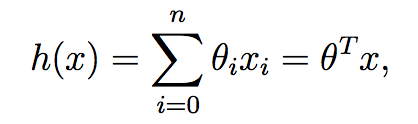
上式中,我们把θ和x都看做向量,这里其实是行向量,θT是θ的转置(即对应的列向量)。这里之所以要转成列向量,是因为要把两个向量的数量积看做是两个矩阵相乘。
有了函数表达式,接下来就是要利用训练集把参数θ学习出来。为此,我们定义代价函数(cost function)如下:
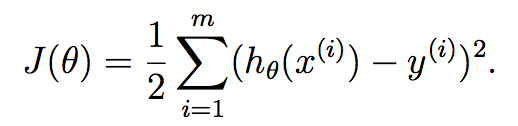
为什么这样定义代价函数呢?如果以前看过最小二乘法(least-squres),就会很熟悉上式。
LMS(Least Mean Square,最小均方)算法
我们需要找出使得代价J(θ)最小的θ。为此,我们估算一个θ的初始值,并不断改变它使得J(θ)更小,直到J(θ)不能再小。具体做法是利用梯度下降(gradient descent)算法,给θ赋一个初始值,然后按照如下表达式不断更新:
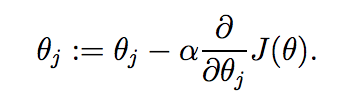
上式更新对θ向量的每个分量θj(j=0,...,n)是同时进行的,其中α叫做学习率(learning rate)。 接下来,我们需要解出右边的偏导(partial derivative),不失一般性地,先假设训练集中只有一个样本(x, y),这样,我们就可以忽略J(θ)中的累加运算,得到如下计算过程,这里需要熟悉导数运算法则,另外,求导的关键在于,对谁求导,谁就是变量,其他都是常量:
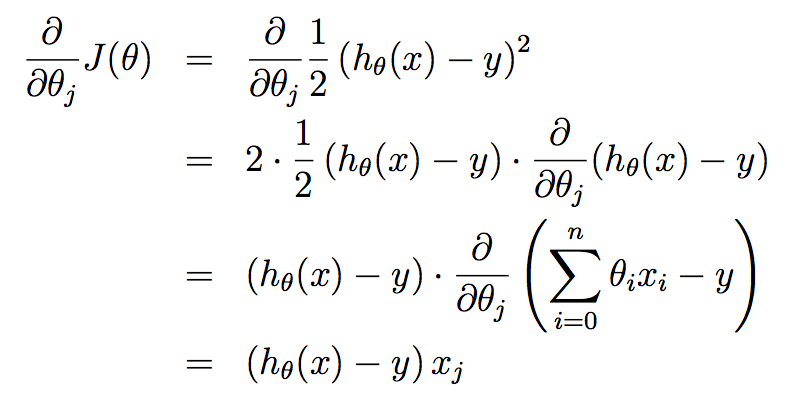
把计算后的偏导代回原式,就可以得到如下更新规则(即LMS更新规则),也叫Widrow-Hoff学习规则:
![]()
从上式更新规则可以看出,θj的更新增量α(y(i)-hθ(x(i)))xj(i)跟y(i)-hθ(x(i))成正比。通俗来讲就是,当预测值hθ(x(i))接近真实值y(i),即误差(error)越小时,参数θj需要做出的更新越小,反之同理。上述更新规则是通过一个样本计算出来的,推广到m个样本呢?有两种方法,第一种就是把之前的累加运算补回来(因为和的导数等于导数的和),如下:
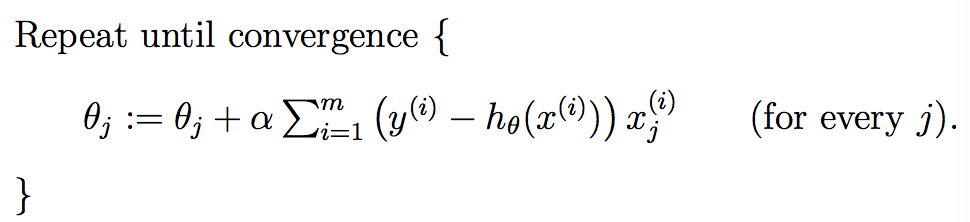
批量梯度下降(batch gradient descent)。
标准方程(normal equations)
矩阵微分(matrix derivatives)
分类和逻辑回归
接下来,我们看看二元分类(binary classification)问题,即预测值y=0或1。0也叫负类(negative class),1则叫正类(positive class)。二元分类中用到的原理同样适用于多元分类。另外,样本(x(i), y(i))中的y(i)也叫做类标(label)。
sigmoid函数
广义线性模型(generalized linear models)
softmax回归
参数拟合(parameter fitting),对数似然(log-likelihood)
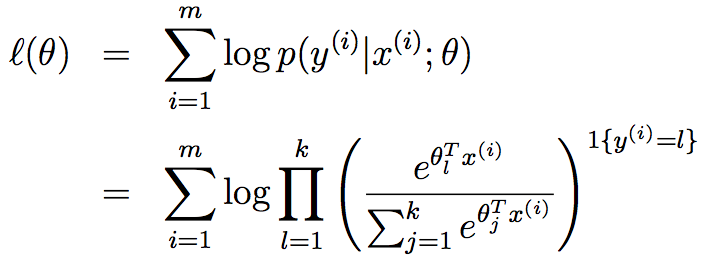
原文链接:
http://cs229.stanford.edu/notes/cs229-notes1.pdf