JDOJ-P1260 VIJOS-P1083 小白逛公园

首先，在这里给大家推荐一个网站，https://neooj.com:8082,这是我母校的网站

言归正传，题目描述

VIJOS-P1083 小白逛公园

Time Limit: 1 Sec Memory Limit: 128 MB

Description

小新经常陪小白去公园玩，也就是所谓的遛狗啦…在小新家附近有一条“公园路”，路的一边从南到北依次排着n个公园，小白早就看花了眼，自己也不清楚该去哪些公园玩了。一开始，小白就根据公园的风景给每个公园打了分。小新为了省事，每次遛狗的时候都会事先规定一个范围，小白只可以选择第a个和第b个公园之间（包括a、b两个公园）选择连续的一些公园玩。小白当然希望选出的公园的分数总和尽量高咯。同时，由于一些公园的景观会有所改变，所以，小白的打分也可能会有一些变化。那么，就请你来帮小白选择公园吧。

Input

第一行，两个整数N和M，分别表示表示公园的数量和操作（遛狗或者改变打分）总数。接下来N行，每行一个整数，依次给出小白开始时对公园的打分。接下来M行，每行三个整数。第一个整数K，1或2。K=1表示，小新要带小白出去玩，接下来的两个整数a和b给出了选择公园的范围（1≤a,b≤N）；K=2表示，小白改变了对某个公园的打分，接下来的两个整数p和s，表示小白对第p个公园的打分变成了s（1≤p≤N）。其中，1≤N≤500 000，1≤M≤100 000，所有打分都是绝对值不超过1000的整数。

Output

小白每出去玩一次，都对应输出一行，只包含一个整数，表示小白可以选出的公园得分和的最大值。

Sample Input

5 3

-3

1 2 3

2 2 -1

1 2 3

Sample Output

-1

思路

　　注：以下写的i代表的是一个左儿子的编号，i+1代表的是一个右儿子的编号，new代表的是他俩的父亲

　　对于这道题目，是区间查询单点修改。又由于数据范围比较大，所以很容易分析出来用线段树进行维护。

　　再分析应该怎么维护每一个区间，这道题应该维护四个状态，区间和sumi，从左开始最大连续和lefti，从右开始最大连续和righti，以及在这个区间中最大连续和maxi，具体如左图所示　　　　

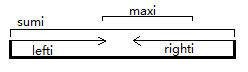
　　对于建树，难的是怎么可以合并这些节点，如右图所示，每两个节点就可以这样合并，首先解释一下如何合并出来新的节点的左边连续最大和，可以看出，左面的和（sumi）加上右面的最大左边连续和（left（i+1）），也就是new_left1，但是这只是一种可能，还有一种可能是就是左边节点的左边最大连续和，这两个值取max，left（new）=max（new_left1，lefti）；同样右边也是这样求，right（new）=max（new_right1，righti）；求和好求，直接加就好啦，sum（new）=sumi+sum（i+1）；求max就不太好求了，由于左儿子的右边最大和右儿子的左边最大可以合并，所以我又开了一个new_max1，max（new）=max（new_max1，maxi，max（i+1））。

　　修改比较好修改，直接找到当前节点O（1）修改就好了，但要注意的是，修改过后我们需要重新维护一下当前点以及当前点以上与这个点有关的所有点，维护过程就是之前建树的过程，时间复杂度O（n*log（n））；查询比较复杂，搜索区间和查询区间有三种情况（如下图）对于这三种情况进行以下讨论，会轻松的发现，当find_r>mid=（dfs_l+dfs_r）>>1时，应该便利右儿子，同理当find_l<=mid=（dfs_l+dfs_r）>>1时，应该便利左儿子，当查询区间完全包含搜索区间时，便没有必要查询，直接返回。当然本题是要查最大值，然而最大连续段有可能横跨多个区间，所以可以在找到的小节点上再建一棵线段树，最后直接输出新线段树的根节点信息就可以了，顺便说一下新的节点的建树和原本的建树一样，由于新的节点即答案的新线段树不好用数组写法，所以我用了动态开点线段树，而基础线段树用的是数组写法。

  1 #include<stdio.h>
  2 int left[2000001];
  3 int right[2000001];
  4 int sum[2000001];
  5 int max[2000001];
  6 int cnt;
  7 int ans_left[1000001];
  8 int ans_right[1000001];
  9 int ans_sum[1000001];
 10 int ans_max[1000001];
 11 int ans_lson[1000001];
 12 int ans_rson[1000001];
 13 void swap(int &a,int &b)
 14 {
 15     int tmp=a;
 16     a=b,b=tmp;
 17 }
 18 int max1(int a,int b)
 19 {
 20     if(a>b)
 21         return a;
 22     return b;
 23 }
 24 void preserve(int p)
 25 {
 26     max[p]=max1(max[p<<1],max[(p<<1)+1]);
 27     max[p]=max1(max[p],right[p<<1]+left[(p<<1)+1]);
 28     left[p]=max1(sum[p<<1]+left[(p<<1)+1],left[p<<1]);
 29     right[p]=max1(sum[(p<<1)+1]+right[p<<1],right[(p<<1)+1]);
 30     sum[p]=sum[p<<1]+sum[(p<<1)+1];
 31 }
 32 void build(int l,int r,int p)
 33 {
 34     if(l==r)
 35     {
 36         int a;
 37         scanf("%d",&a);
 38         left[p]=sum[p]=right[p]=max[p]=a;
 39         return;
 40     }
 41     build(l,(l+r)>>1,p<<1);
 42     build(((l+r)>>1)+1,r,(p<<1)+1);
 43     preserve(p);
 44 }
 45 void update(int p,int l,int r,int place,int delta)
 46 {
 47     if(l==r)
 48     {
 49         left[p]=sum[p]=right[p]=max[p]=delta;
 50         return;
 51     }
 52     int mid=(l+r)>>1;
 53     if(place<=mid)
 54         update(p<<1,l,mid,place,delta);
 55     else
 56         update((p<<1)+1,mid+1,r,place,delta);
 57     preserve(p);
 58 }
 59 void find(int p,int l,int r,int x,int y)
 60 {
 61     int place=++cnt;
 62     ans_lson[place]=ans_rson[place]=ans_sum[place]=0;
 63     if(l>=x&&r<=y)
 64     {
 65         ans_max[place]=max[p];
 66         ans_sum[place]=sum[p];
 67         ans_left[place]=left[p];
 68         ans_right[place]=right[p];
 69         return;
 70     }
 71     int mid=(l+r)>>1,times=0;
 72     if(x<=mid)
 73     {
 74         ans_lson[place]=cnt+1;
 75         find(p<<1,l,mid,x,y);
 76         times++;
 77         ans_max[place]=ans_max[ans_lson[place]];
 78         ans_sum[place]=ans_sum[ans_lson[place]];
 79         ans_left[place]=ans_left[ans_lson[place]];
 80         ans_right[place]=ans_right[ans_lson[place]];
 81     }
 82     if(y>mid)
 83     {
 84         ans_rson[place]=cnt+1;
 85         find((p<<1)+1,mid+1,r,x,y);
 86         times++;
 87         ans_max[place]=ans_max[ans_rson[place]];
 88         ans_sum[place]=ans_sum[ans_rson[place]];
 89         ans_left[place]=ans_left[ans_rson[place]];
 90         ans_right[place]=ans_right[ans_rson[place]];
 91     }
 92     if(times==2)
 93     {
 94         int son_l=ans_lson[place];
 95         int son_r=ans_rson[place];
 96         ans_max[place]=max1(ans_max[son_l],ans_max[son_r]);
 97         ans_max[place]=max1(ans_max[place],ans_right[son_l]+ans_left[son_r]);
 98         ans_left[place]=max1(ans_sum[son_l]+ans_left[son_r],ans_left[son_l]);
 99         ans_right[place]=max1(ans_sum[son_r]+ans_right[son_l],ans_right[son_r]);
100         ans_sum[place]=ans_sum[son_l]+ans_sum[son_r];
101     }
102 }
103 int main()
104 {
105     int n,m;
106     scanf("%d%d",&n,&m);
107     build(1,n,1);
108     for(int i=1;i<=m;i++)
109     {
110         int kind,a,b;
111         scanf("%d%d%d",&kind,&a,&b);
112         if(kind==1)
113         {
114             if(a>b)
115                 swap(a,b);
116             for(int i=1;i<=cnt;i++)
117                 ans_max[i]=ans_right[i]=ans_left[i]=ans_sum[i]=(int)-1e9;
118             cnt=0;
119             find(1,1,n,a,b);
120             printf("%d
",ans_max[1]);
121         }
122         else
123             update(1,1,n,a,b);
124     }
125 }