1、概率图模型: Bayesian Networks

　　整个专栏对最近学习的概率图模型（Probabilistic Graphical Models）做一个总结，本篇主要总结Bayesian Networks的基本原理。

1、对于多变量的分布

　　PGM的主要目的是提供一种有效的工具来解约多概率变量模型。用联合概率来表示多概率变量模型如下：

　　　　　　　　　　　　　　　　　　　　　　　　　　P(X₁,X₂,...,X_n)                                                    (1)

　　PGM的方法是把这个联合概率变成条件概率。一个简单的例子，可以表示成：

　　　　　　　　　　　　　　　　　　　P(X₁,X₂,...,X_n) = P(X₁)P(X₂|X₁)P(X₃|X₁,X₂)...P(Xn|X₁...X_n-1)         (2)

　　公式（2）中所有的variable（X_1，X₂等）之间都不独立，假设另一种极端的情况所有的variable之间全部独立的情况，则条件概率分布（CPD）可以表示成：

　　　　　　　　　　　　　　　　　　　             P(X₁,X₂,...,X_n) = P(X₁)P(X₂)...P(X_n)                     (3)

　　对于公式（2）中的情况，假设一共有n个variable，每一个variable中有k个values，因为其是依赖关系因此一共有 kⁿ种情况，因为对于X1有k种取值的情况，那么在X1已知的前提之下，X2也是有五种情况，两个variables组成一个二维的向量，共有k²种情况，依次类推，其数量级便是kⁿ。但是对于相互独立的事件而言，共有nk中情况，每个时间都是独立的，每一个variable的选择都是C¹_K，比起公式（2）数量级大大的减小。但是在大多数现实情况中，并不是这样的，PGM模型通常会取两者的中间地带，在计算效率和合理的建模能力之间折中。

2、例子The Dishonest Casino

　　假设一种赌场游戏，有两个骰子，一个是Fair Die，1-6数字出现的概率是相同的；另一个是Loaded die，1-5出现的概率是1/10，6出现的概率是1/2。Casino player在两个骰子之间进行切换。每次下注1美元，你用Fair Die骰子，每次和Casino player比较大小，数字大的人可以得到两个人的赌注2美元。

　　给出Casino player投出骰子的序列：

　　124552 6 4 6214 614 613 613666 166 466 1 6 366 1 6 366 1 6 3 6 1 6515 61511514 61235 62344

　　问题：（1）投出该序列的可能性？（EVALUATION problem 评估问题）

　　　　　（2）序列哪一部分是用Loaded die投的？（DECODING question 解码问题）

　　　　    （3）Casino player切换骰子的频率？（LEARNING question 学习问题）

　　针对这几个问题：

　　　　　 （1）选择variables：X_n——表示第n次投掷骰子的结果；Y_n——表示第n次是否是用Loaded die投掷的，其中X是已知的，Y是未知的。

　　　　　 （2）选择结构：模型如下图，假设对骰子的选择是我们的一种策略，所以Yt和Yt+1是相关的，并且每次的投掷数与骰子有关Yt → Xt。

　　　　　 （3）选择概率：P(Yt+1|Yt)，P(Xt|Yt)

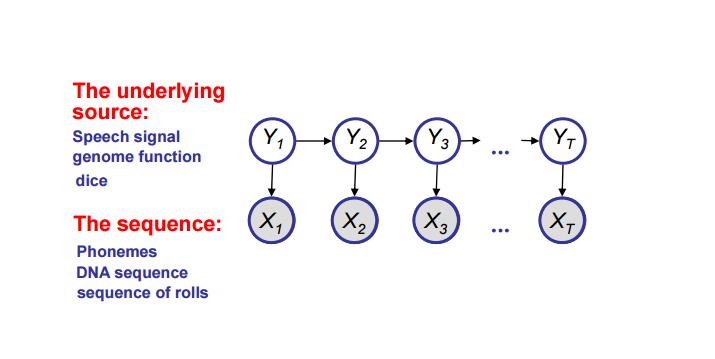
图1（取自CMU 10708课程）

　　因此可以求得联合概率分布：

　　　　p(x,y) = p(x1,...,xT,y1,...,yT) = p(y1)p(y2|y1)...p(yT|yT-1)p(x1|y1)p(x2|y2)...p(xT|yT)

　　　　　　   = p(y1,...,yT)p(x1,...,xT|y1,...,yT)

　　　　因此可得边缘概率：p(x) = ∑_y p(x,y)

　　　　后验概率：p(y|x) = p(x,y) / p(x)

3、贝叶斯网络

　　贝叶斯网络是一种PGM模型，是有向开环图（DAG），用来表示variables之间的条件依赖关系和独立关系。节点表示variables，有向边表示两个variable之间的依赖关系。

　　3-1、因式分解

　　　　　　　　　　　　　　         P(X1, X2, . . . , Xn) = ∏_i=1:nP(Xi |Parents(Xi)）

　　3-2、独立性

　　对于variables X,Y，若两者相互独立，则满足：P(A,B) = P(A)P(B) , P(A|B) = P(A) , P(B|A) = P(B)，在贝叶斯网络中，如下图网络是一个学生的各种关系图，Difficulty表示考试的难度，Intelligence表示学生的天赋，这两个决定了学生的成绩Grade，成绩决定了学生可以拿到什么样的推荐信Letter，Intelligence决定了学生会有怎样的SAT成绩等等。在网络中有几种流动形式X->Y , X<-Y , X->W->Y , X<-W<-Y , X<-W->Y , X->W<-Y。

　　X->Y和Y->X一定是相互依赖的，其他几种情况的依赖情况如下表所示，√表示链是激活的，即X、Y之间有依赖关系，×表示链是未激活的，即X、Y之间是相互独立的关系，拿最后一个V型结构来举例，Difficulty->Grade<-Intelligence这一条线上，其中学生的成绩是已知的了，那么如果课程的难度越难，成绩一定的情况下，说明这个同学越聪明、能力越强，Difficulty与Intelligence之间是相互影响的，没有独立；但是如果学生的成绩未知，那么考试的难度是和学生的智力完全没有关系的两件事，因此Difficulty与Intelligence之间是相互独立的。

	W未知	W已知
X->W->Y	√	×
X<-W<-Y	√	×
X<-W->Y	√	×
X->W<-Y	×	√

图2（取自coursera Stanford PGM课程）

　　总结：对于一条链，X1->X2->...->Xk，如果这条链是激活的，那么满足下面两个条件

　　　　  （1）对于任何的V型结构，Xi-1 -> Xi <- Xi+1，Xi 或者其子孙节点至少有一个是已知的；

　　　　  （2）对于任何的V型结构，Xi-1 -> Xi <- Xi+1，除了Xi 其他均未知。

　　3-3、I-maps

　　定义：如果图G中的所有依赖独立性分布，在分布P中全部能够找到，那么G就叫做分布P的I-map，I 表示依赖独立分布的集合， I(G)为I(P)的子集，及P中有的依赖独立分布可能图G中没有，但是图G中所有的依赖独立分布，在P中全部能够找到。

　　依赖独立（D-separated）即在已知Z的情况下，A和B无通路，则A与B依赖独立。基座d-sep_G(x,y|z) 等价于 P：（x⊥y|z）。

　　在一个图G中，如果给定了节点Xi的父节点，那么它与除了其后裔节点的所有节点依赖独立，以图2为例，如果已知了Letter的父节点Grade，那么Letter与Difficulty、Intelligence、Coherence依赖独立。更多对于D-separated的解释可见博客：https://my.oschina.net/dillan/blog/134011

　　3-4、P-maps

　　定义：如果 I(P) = I(G)，则图G叫做概率分布P的p-map（perfect map）。

　　并不是每一个概率分布P都有p-map，例如：

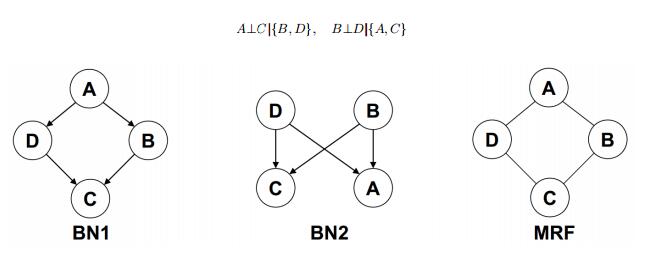
图3（取自http://www.cs.cmu.edu/~epxing/Class/10708-14/scribe_notes/scribe_note_lecture3.pdf）

　　对于图顶显示的两个概率分布，BN1不能满足B⊥D | A , BN2不能满足B⊥D | C的条件，但是马尔科夫网络可以表示，马尔科夫网络比起贝叶斯网络有更好的表现性。