任何实际的信道都不是理想的,在传输信号时会产生各种失真以及带来多种干扰。
数字通信的优点就是在接受端只要能够从失真的波形识别出原来的信号,那么这种失真对通信质量就没有影响。

上图中信号通过实际信道后虽然有失真,但在接收端还可以识别出原来的码元。

上图中,通过信道后,码元的波形已经严重失真,接收端已经不能识别码元时0还是1。
码元传输速度越高,或信号传输的距离越远,或噪声干扰越大,或传输媒体质量越差,在信道的接收端,波形的失真就越严重。
影响信道上的数字信息传输速率的因素有两个:码元的传输速度和每个码元承载的比特信息量。
码元的传输速率受信道能够通过的频率范围影响,每个码元承载的比特信息量则受信道的信噪比影响。
(1)信道能够通过的频率范围
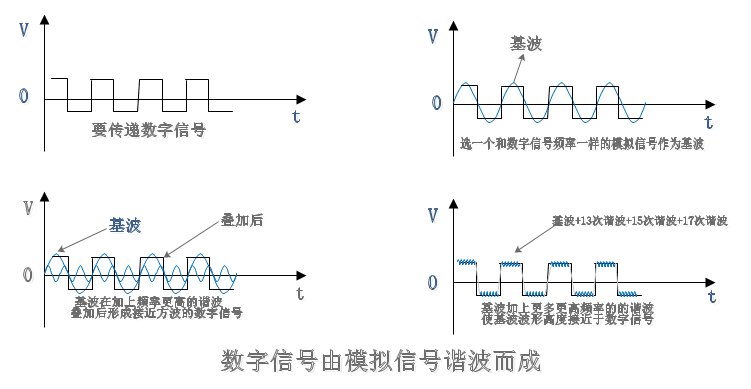
在信道上传输的数字信号其实是使用多个频率的模拟信号进行多次谐波而成的方波,如图所示。
假如数字信号频率位1000Hz,需要使用1000Hz的模拟信号作为基波,基本信号和更高频率谐波叠加形成数字信号的波形。
经过多次更高频率的波进行谐波,可以形成接近数字信号的波形,现在大家应该明白了为什么数字信号中包含更高频率的谐波了。

具体的信道所能通过的模拟信号的频率范围总是有限的。能够通过的最高频率减去最低频率就是该信道的带宽。
如图所示的电话线,假定其允许频率范围从300~3300Hz的模拟信号能够通过,低于300Hz和高于3300Hz的模拟信号均不能通过,则电话线的带宽位3000Hz。

前面讲了模拟信号通过信道的频率是有一定范围的,如上图所示。
数字信号通过信道,数字信号中高频分量(高频模拟信号)有可能不能通过信道或者衰减,接收到的波形前沿和后沿就变得不那么陡峭。
码元之间所占用的时间界限也不再明显,而是前后都拖了尾巴。这样在接收端收到的信号波形就失去了码元之间清晰的界限,这种现象叫做“码间串扰”。
严重的码间串扰将使得本来分得很清楚的一串代码变得模糊而无法识别。
早在1924年,奈奎斯特就推导出了著名的耐氏法则。
他给出了在假定的理想条件下,为了避免码间串扰,码元的传输速率的上限值。
在任何信道中,码元的传输速率是有上限的,否则就会出现码间串扰的问题,使接收端对码元的判决(即识别)称为不可能。
如果信道的频带越宽,也就是能够通过的信号高频分量越多,那么就可以使用更高速率传递码元而不会出现码间串扰。
理想低通信道的最高码元传输速率=2WBaud w是理想低通信道的带宽,单位是Hz。 Band是波特,是码元传输速率的单位。
使用奈氏准则给出的公式,可以根据信道的带宽,计算出码元的最高传输速率。
(2)信噪比
既然代码的传输速率有上限,如果打算让信道更快的传输信息,就需要让一个码元承载更多的比特信息量。
有二进制码元,一个码元代表一个比特,八进制码元,一个码元表示三比特,十六进制码元,一个码元表示四比特。
要是可以无限提高一码元携带比特信息量,信道传输数据的速率岂不是可以无线提高?其实信道传输信息的能力也是有上限的。
噪声存在于所有的电子设备和通信信道中。由于噪声是随机产生的,它的瞬时值有时会很大。
在电压范围一定的情况下,十六进制码元波形之间的差别要比八进制码元波形之间的差别小。
在真实信道传输由于噪声干扰,码元波形差别太小的在接受端就不易清晰的识别。
信道的极限信息传输速率受那些因素影响了。下面我们来看看香农公式。
噪音的影响是相对的,如果信号相对较强,那么噪声的影响就相对较小。因此信噪比就很重要。
所谓信噪比就是信号的平均功率和噪声的平均功率之比,常记为S/N,并用分贝(dB)作为度量单位。即
信噪比(dB) =10log10(S/N)(dB)
例如,当S/N=10时,信噪比为10dB;而当S/N=1000时,信噪比为30dB。
在1948年,信息论的创始人x香农推导出著名的香农公式。香农公式指出:信道的极限信息传输速率C是:
C = Wlog2(1+S/N) (b/s)
式中,w为信道的带宽(以Hz为单位);s为信道内所传信号的平均功率;N为信道内部的高斯噪声功率。
香农公式表明,信道的带宽或信道中的信噪比越大,信息的极限传输速率就高。
香农公式的意义在于:只要信息传输速率低于信道的极限信息传输速率,就一定可以找到某种方法来实现无差错的传输。