机器学习系列（6） 逻辑回归

逻辑回归

一、逻辑回归的适用性：

优点：

1. 逻辑回归对线性关系的拟合效果好
2. 逻辑回归拟合和计算非常快
3. 逻辑回归返回的分类结果不是固定的0,1，而是以小数的方式出现，可以把结果当成连续数据来使用

缺点：

对数据和场景要求高

二、逻辑回归的基本原理

2.1 什么是逻辑回归

面对一个分类问题，建立一个代价函数，然后通过优化方式迭代求解出最优的模型参数，然后测试验证我们这个求解的模型的好坏。

2.2 逻辑回归步骤

• 寻找预测函数h

构造的预测函数形式为sigmoid函数，形式为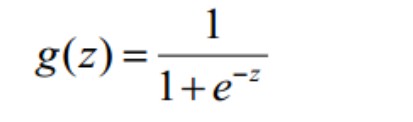

• 构造损失函数j

• 想办法使得J函数最小并求得回归参数

三、sklearn实现逻辑回归

from sklearn.linear_model import LogisticRegression as LR
from sklearn.datasets import load_breast_cancer
import numpy as np
import matplotlib as plt
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

data = load_breast_cancer()
X = data.data
y = data.target

# 重要参数 penalty & C
# penalty：可以输入l1或者l2来指定使用哪一种正则化方式，不写默认l2
# C： C越小，损失函数越小，模型对损失函数惩罚越严重
# max_iter：梯度下降
lrl1 = LR(penalty='l1', solver='liblinear',C=0.5, max_iter=1000)
lrl2 = LR(penalty='l2', solver='liblinear',C=0.5,max_iter=1000)
# 逻辑回归coef_，可以查看每个特征对应的参数
lrl1 = lrl1.fit(X,y)
lrl1.coef_
lrl2 = lrl2.fit(X,y)
lrl2.coef_
# 在实际使用中，基本上默认L2正则化，如果效果不好，就换l1试试

'''
处理样本不均衡的问题，主流的是采样法，通过重复样本的方式来平衡标签，可以进行上采样（增加少数类的样本)，或者下采样（减少少数类的样本)，
对于逻辑回归，上采样时最好的办法
'''