Apriori 算法需要多次扫描数据,I/O是很大的瓶颈。为了解决这个问题,FP Growth 算法采用了一些技巧,无论多少数据,只需要扫描两次数据集即可。
FP Tree数据结构
为了减少 I/O 次数,FP Tree 算法引入了一些数据结构来临时存储数据。这个数据结构包括三部分,如下图所示:
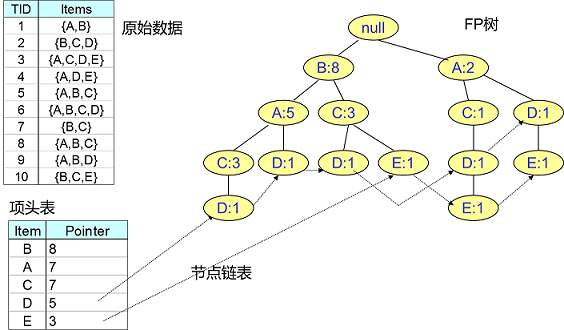
1)项头表:里面记录了所有的 $1$ 项频繁集出现的次数,按照次数降序排列。比如上图中 $B$ 在所有 $10$ 组数据中出现了 $8$ 次,因此排在第一位。
2)FP Tree:它将我们的原始数据集映射到了内存中的一颗 FP 树,这个 FP 树比较难理解,它是怎么建立的呢?这个我们后面再讲。
3)节点链表:所有项头表里的 $1$ 项频繁集都是一个节点链表的头,它依次指向 FP 树中该 $1$ 项频繁集出现的位置。
项头表的建立
1)第一次扫描数据,得到所有频繁一 $1$ 项集的的计数。然后删除支持度低于阈值的项,将 $1$ 项频繁集放入项头表,并按照支持度降序排列。
2)第二次也是最后一次扫描数据,将读到的原始数据剔除非频繁 $1$ 项集,并按照支持度降序排列。
举个例子,我们有 $10$ 条数据,如下图所示:
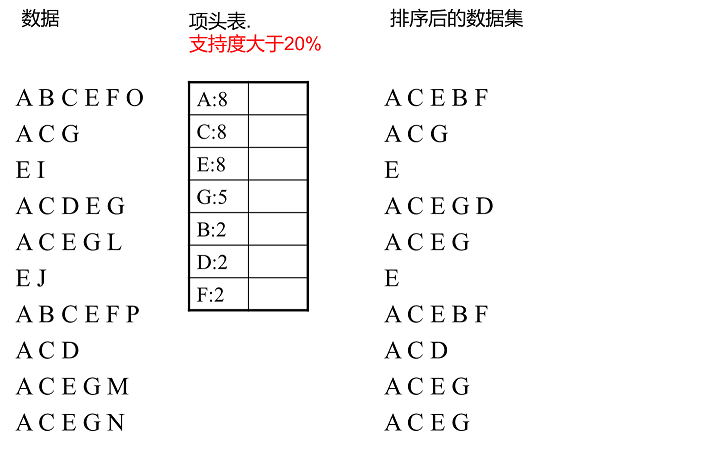
a. 第一次扫描数据并对 $1$ 项集计数,我们发现 $O,I,L,J,P,M,N$ 都只出现一次,支持度低于 20% 的阈值,因此他们不会出现
在下面的项头表中。剩下的 $A,C,E,G,B,D,F$ 按照支持度的大小降序排列,组成了我们的项头表。
b. 接着我们第二次扫描数据,对于每条数据剔除非频繁1项集,并按照支持度降序排列。比如数据项 $ABCEFO$,里面 $O$ 是非频繁 $1$ 项集,
因此被剔除,只剩下了 $ABCEF$。按照支持度的顺序排序,它变成了 $ACEBF$。其他的数据项以此类推。为什么要将原始数据集里的频
繁 $1$ 项数据项进行排序呢?这是为了我们后面的 FP 树的建立时,可以尽可能的共用祖先节点。
FP Tree的建立
有了项头表和排序后的数据集,我们就可以开始 FP 树的建立了。开始时 FP 树没有数据,建立 FP 树时我们一条条的读入排序后的数据集,
插入 FP 树,插入时按照排序后的顺序,排序靠前的节点是祖先节点,而靠后的是子孙节点。如果有共用的祖先,则对应的公用祖先节点计
数加 $1$。插入后,如果有新节点出现,则项头表对应的节点会通过节点链表链接上新节点。直到所有的数据都插入到 FP 树后,就建立完成。
还是用上面的例子来描述:
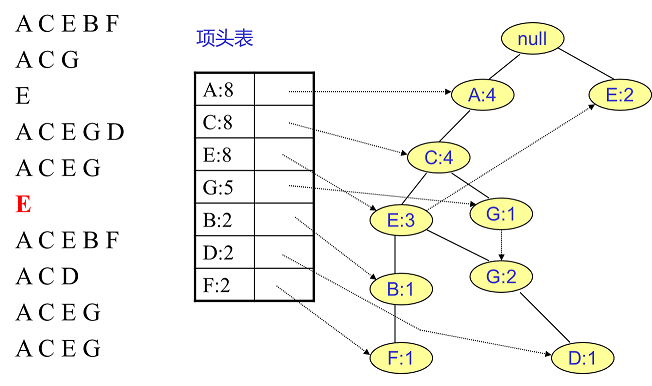
首先,我们插入第一条数据 $ACEBF$,如下左图所示。此时 FP 树没有节点,因此 $ACEBF$ 是一个独立的路径,所有节点计数为 $1$, 项头
表通过节点链表链接上对应的新增节点。
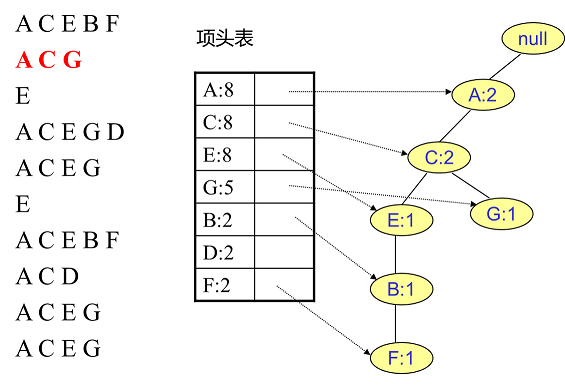
接着我们插入数据 $ACG$,如下右图所示。由于 $ACG$ 和现有的 FP 树可以有共有的祖先节点序列 $AC$,因此只需要增加一个新节点 $G$,将
新节点 $G$ 的计数记为 $1$。同时 $A$ 和 $C$ 的计数加 $1$ 成为 $2$。当然,对应的 $G$ 节点的节点链表要更新

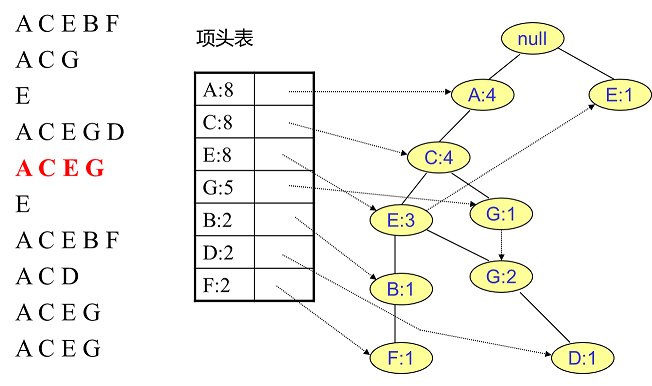
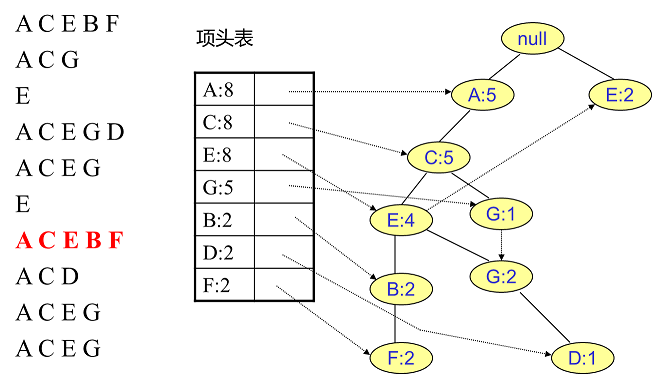
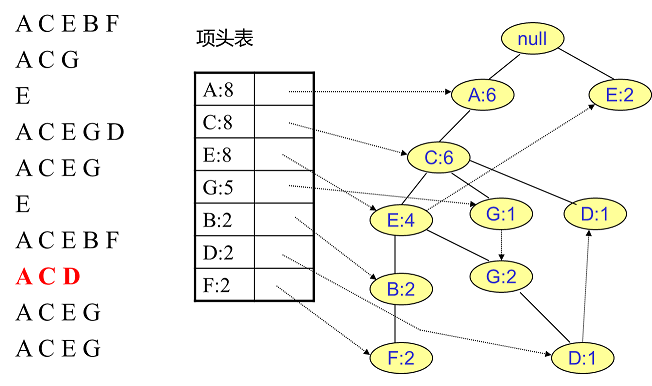
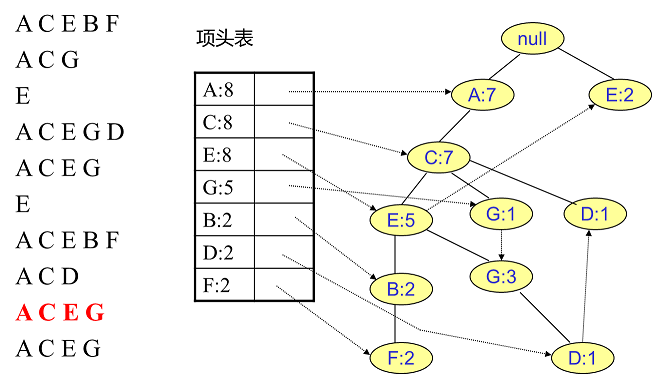
同样的办法可以更新后面 $8$ 条数据,如下 $8$ 张图(从左到右,从上到下阅读)。


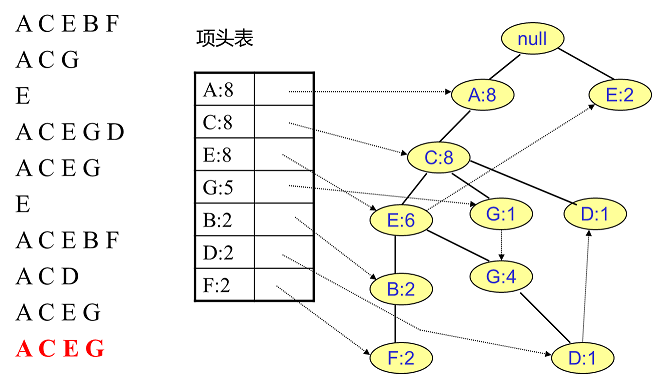
FP Tree的挖掘
得到了 FP 树和项头表以及节点链表,我们首先要从项头表的底部项依次向上挖掘。对于项头表对应于FP树的每一项,我们要找到它的条件模式基。
所谓条件模式基是以我们要挖掘的节点作为叶子节点所对应的 FP 子树。得到这个 FP 子树,我们将子树中每个节点的的计数设置为叶子节点的计数,
并删除计数低于支持度的节点。从这个条件模式基,我们就可以递归挖掘得到频繁项集了。
怎么理解呢?
一开始遍历了一次数据库得到频繁 $1$ 项集,但现在我们还想得到频繁 $2$ 项集,频繁 $3$ 项集等,直到找出最长的频繁多项集,利用的思想就是:
任意一个 $k$ 项集,它一定是以频繁 $1$ 项集中的元素结尾的。所以,我们只要找出以项头表中元素结尾的所有频繁多项集即可。
还是以上面的例子来讲解。
我们看看先从最底下的 $F$ 节点开始,我们先来寻找 $F$ 节点的条件模式基,由于 $F$ 在 FP 树中只有一个节点,因此候选就只有下图左所示的一条路径,
对应 $left { A:8,C:8,E:6,B:2,F:2 ight }$。我们接着将所有的祖先节点计数设置为叶子节点的计数,即 FP 子树变成 $left { A:2,C:2,E:2,B:2,F:2 ight }$。一般
我们的条件模式基可以不写叶子节点,因此最终 $F$ 的条件模式基如下图所示。

通过它,我们很容易得到所有以 $F$ 结尾的频繁多项集:
1)频繁 $2$ 项集:$left { A:2,F:2 ight }, left { C:2,F:2 ight },left { E:2,F:2 ight },left { B:2,F:2 ight }$。
2)频繁 $3$ 项集:$left { A:2,C:2,F:2 ight }, left { A:2,E:2,F:2 ight },left { A:2,B:2,F:2 ight },left { C:2,E:2,F:2 ight },left { C:2,B:2,F:2 ight },left { E:2,B:2,F:2 ight }$
还有以 $F$ 结尾的频繁 $4$ 项集,频繁 $5$ 项集,就不写了,无非就是排列组合而已。当然一直递归下去,最长的频繁项集为频繁 $5$ 项集,为
$left { A:2,C:2,E:2,B:2,F:2 ight }$。
$F$ 挖掘完了,我们开始挖掘 $D$ 节点。$D$ 节点比 $F$ 节点复杂一些,因为它有两个叶子节点,得到的 FP 子树如下图所示。
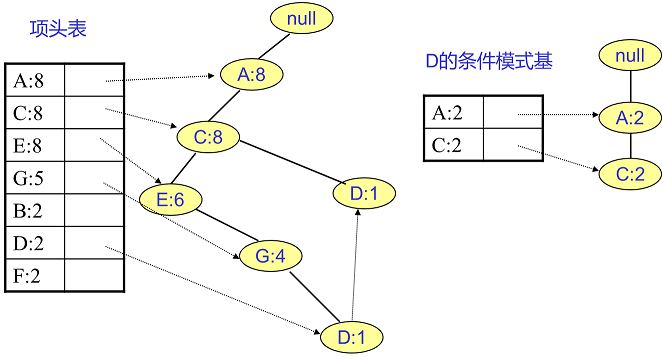
我们接着将所有的祖先节点计数设置为叶子节点的计数,即变成 $left { A:2, C:2,E:1, G:1,D:1, D:1 ight }$,此时 $E$ 节点和 $G$ 节
点由于在条件模式基里面的支持度低于阈值,被我们删除,最终在去除低支持度节点并不包括叶子节点后D的条件模式基为 $left { A:2, C:2 ight }$。
通过它,我们很容易得到以 $D$ 结尾的频繁多项集,对应的最大的频繁项集为频繁 $3$ 项集 $left { A:2,C:2,D:2 ight }$。
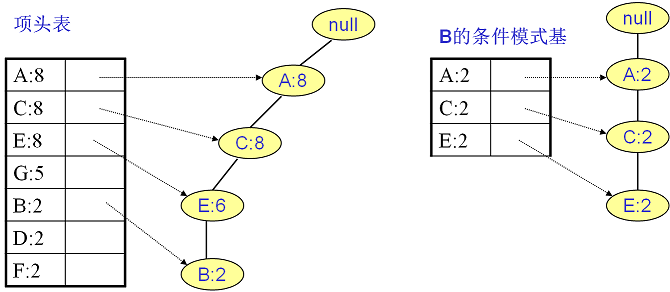
同样的方法可以得到 $B$ 的条件模式基如下图左图,递归挖掘到 $B$ 的最大频繁项集为频繁 $4$ 项集 $left { A:2, C:2, E:2,B:2 ight }$。
继续挖掘 $G$ 的频繁项集,挖掘到的 $G$ 的条件模式基如下图右图,递归挖掘到 $G$ 的最大频繁项集为频繁 $4$ 项集 $left { A:5, C:5, E:4,G:4 ight }$。
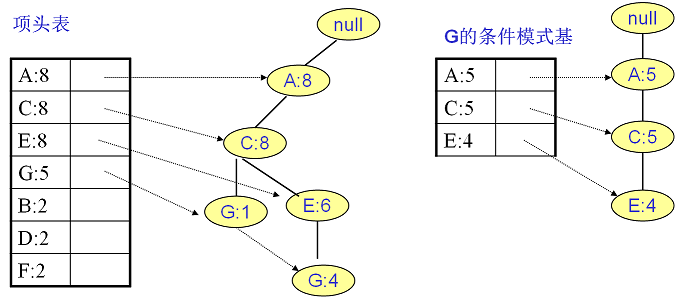
$E$ 的条件模式基如下左图,递归挖掘到 $E$ 的最大频繁项集为频繁 $3$ 项集 $left { A:6, C:6, E:6 ight }$。
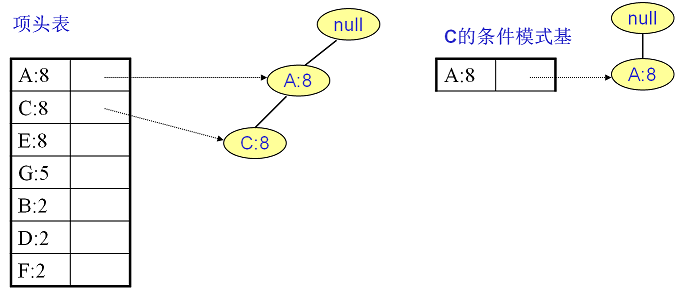
$C$ 的条件模式基如下右图,递归挖掘到 $C$ 的最大频繁项集为频繁 $2$ 项集 $left { A:8, C:8 ight }$。

从上面的分析可以看到,最大的频繁项集为5项集。包括 $left { A:2, C:2, E:2,B:2,F:2 ight }$。