Apriori 算法是常用的用于挖掘出数据关联规则的算法,它用来找出数据值中频繁出现的数据集合,找出这些集合的模式有助于我们做一些决策。
频繁项集的评估标准
什么样的数据才是频繁项集呢?一起出现次数多的数据集就是频繁项集吗!的确,这也没有说错,但是有两个问题:
1)当数据量非常大的时候,我们没法直接肉眼发现频繁项集,这催生了关联规则挖掘的算法,比如 Apriori, PrefixSpan, CBA。
2)我们缺乏一个频繁项集的标准。比如 $10$ 条记录,里面 $A$ 和 $B$ 同时出现了三次,那么我们能不能说 $A$ 和 $B$ 一起构成频繁项集呢?
因此我们需要一个评估频繁项集的标准。
支持度:几个关联的数据在数据集中出现的次数占总数据集的比重,即几个数据关联出现的概率。如果我们有两个想分析关联性的数据 $X$ 和 $Y$,则
对应的支持度为:
$$Support(X,Y) = P(X,Y)$$
置信度:体现了一个数据出现后,另一个数据出现的概率,或者说数据的条件概率。如果我们有两个想分析关联性的数据 $X$ 和 $Y$,$X$ 对 $Y$ 的置信度为
$$Confidence(X Leftarrow Y) = P(X | Y)$$
提升度:表示含有Y的条件下,同时含有X的概率,与X总体发生的概率之比,即:
$$Lift(X Leftarrow Y) = frac{P(X | Y)}{P(X)} = frac{Confidence(X Leftarrow Y)}{Support(X)}$$
提升度体先了 $X$ 和 $Y$ 之间的关联关系, 提升度大于 $1$,则 $X Leftarrow Y$ 是有效的强关联规则,提升度小于等于 $1$,则 $X Leftarrow Y$ 是无效的强关联规则。
$Apriori$ 算法思路
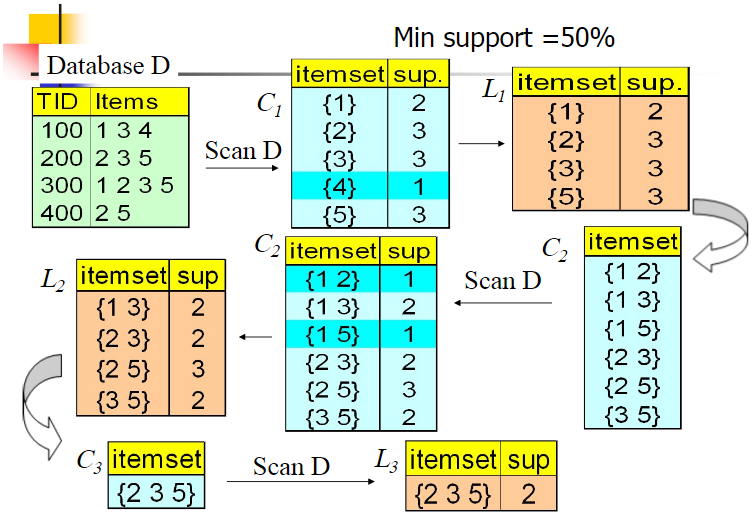
我们的数据集 $D$ 有 $4$ 条记录,现在我们用 $Apriori$ 算法来寻找频繁 $k$ 项集,最小支持度设置为 50%。
1)计算 $5$ 个数据的支持度,生成候选频繁 $1$ 项集 $C_{1}$,然后进行剪枝,数据 $4$ 由于支持度只有 25% 被剪掉,最终的频繁 $1$ 项集为 $L_{1}$。
2)现在我们自连接 $L_{1}$ 生成候选频繁 $2$ 项集,因为每一项的长度要为 $2$,所以连接的两项必须满足只有一个元素不同,连接后生成 $C_{2}$。
3)扫描数据集计算候选频繁 $2$ 项集的支持度,接着进行剪枝,由于 $1,2$ 和 $1,5$ 的支持度只有 25% 而被筛除,得到最终的频繁 $2$ 项集 $L_{2}$。
4)现在我们自连接 $L_{2}$ 生成候选频繁 $3$ 项集,因为生成的每一项只有 $3$ 个元素,所以能够连接的两项必须有 $1$ 个元素相同,如 $1,3$ 和 $2,5$ 就是无法连接的。
5)最终得到的真正频繁 $3$ 项集为 $2,3,5$ 一组。由于此时我们无法再进行数据连接,进而得到候选频繁 $4$ 项集,最终的结果即为频繁 $3$ 三项集 $2,3,5$。
上面的剪枝可以利用 $Apriori$ 的性质:任何一个频繁项集的任一子集也应该是频繁项集。
从算法的步骤可以看出,$Aprior$ 算法每轮迭代都要扫描数据集,因此在数据集很大,数据种类很多的时候,算法效率很低。