阅读本篇之前,可先阅读一下梯度下降法。下面介绍一下牛顿法的基本思路。记原始的函数为 $F(x)$,它对应的二阶泰勒展开式为 $f(x)$
将目标函数 $F(x)$ 进行二阶泰勒展开(如果不了解这个可先阅读博客)得:
$$f(x) = f(x_{0}) + abla f(x_{0})^{T}(x - x_{0}) + frac{1}{2}(x - x_{0})^{T}G(x_{0})(x - x_{0})$$
接下来对这个函数求一阶偏导数和二阶偏导数,如果不知道怎么求,可先阅读以下博客:向量内积求偏导、二次型求偏导、向量对向量求偏导。
函数 $f(x)$ 对列向量 $x$ 求偏导得
$$ abla f(x) = abla f(x_{0}) + G(x_{0})(x - x_{0})$$
这个结果向量是由 $f(x)$ 对各坐标轴的偏导数组成。
将列向量 $ abla f(x)$ 继续对 $x^{T}$ 求偏导,结果为
$$ abla^{2} f(x) = G(x_{0})$$
这个结果矩阵由 $f(x)$ 的各个二阶偏导数组成,即海森矩阵,很明显它是一个与自变量无关的常矩阵。这就很神奇:原函数 $F(x )$在 $x_{0}$ 点
的海森矩阵居然就是泰勒展开式 $f(x)$ 在任一点处海森矩阵(因为是常矩阵,与变量无关了)。
我们知道某点是极值点的必要条件是其一阶偏导数为 $0$,即梯度向量为 $0$,令
$$ abla f(x) = 0$$
这个方程并不一定有解,就算有解,解出来的就一定是局部极小值点吗?很显然不一定,所以牛顿法做了一个极强的假设:每个迭代点或泰勒展开点 $x_{k}$ 处,
矩阵 $G(x_{k})$ 正定。对于第一次迭代,因为 $G(x_{0})$ 正定,故矩阵可逆,所以可解得
$$x_{1} = x_{0} - G^{-1}(x_{0}) abla f(x_{0})$$
那这个点是极小值点吗?因为 $G(x_{0})$ 是正定的,所以泰勒二阶展开式 $f(x)$ 的海森矩阵就是正定矩阵,所以必然存在极小值。
之后将一阶偏导数为 $0$ 的点 $x_{1}$ 作为下一次泰勒二阶展开点,继续求偏导数为 $0$ 的点 $x_{2}$,如此循环。。。
现在,我们来分析下这个新的点对应的函数值 $f(x_{1})$ 是否较原来的 $f(x_{0})$ 小?因为已经假设矩阵 $G(x_{0})$ 正定,所以有
$$- abla f(x_{0})^{T}G^{-1}(x_{0}) abla f(x_{0}) < 0$$
说明向量 $- G^{-1}(x_{0}) abla f(x_{0})$ 和梯度向量的夹角是一个钝角,所以在这个方向上函数值是减少的。
但是我们根本没有办法保证原函数 $f(x)$ 对每一次迭代点的海森矩阵都是正定的,即无法保证牛顿法的每一次迭代方向一定沿着函数值下降的方向。
所以,牛顿法不能保证迭代最终能够收敛。
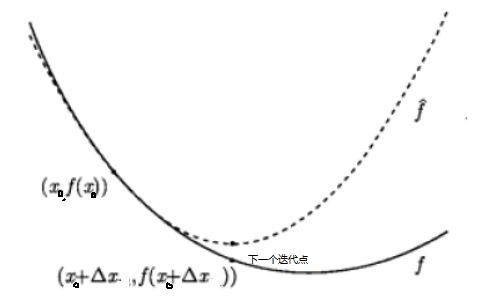
从几何上说,牛顿法就是用一个二次曲面去拟合你当前所处位置的局部曲面,而梯度下降法是用一个平面去拟合当前的局部曲面,通常情况下,二次
曲面的拟合会比平面更好,所以牛顿法选择的下降路径会更符合真实的最优下降路径。