相似是研究线性变换矩阵之间的关系,首先需要确定一个线性空间,这是必要的,研究不同线性空间中变换矩阵的关系没啥意义,确
定了线性空间,那么向量的维数,基中向量的个数都被定下来了。
定义:若 $A$ 和 $B$ 都是 $n$ 阶矩阵,如果存在可逆矩阵 $P$,使得 $P^{-1}AP = B$,则称矩阵 $A$ 与 $B$ 相似,记为 $Asim B$。
理解相似矩阵,得先理解线性变换。
通俗一点来描述相似矩阵:同一个线性变换,不同参考系下的矩阵,称为相似矩阵。
为什么我们需要相似矩阵呢?
对空间中的某一个向量做变换,需要先确定线性空间,并选定一组基来建立坐标系,选择的坐标系越复杂,所做的变换也就越复杂,
计算量也越大,比如,需要将空间中的某一个向量 $alpha$ 逆时针旋转 $45$ 度,下面是选择的几组参考系:
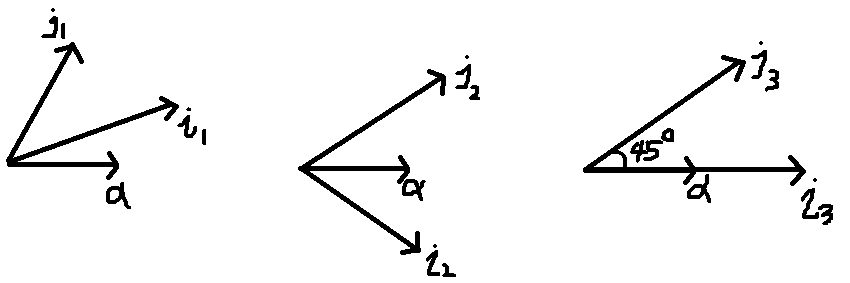
很明显在第三种坐标系,很容易写出向量 $alpha$ 逆时针旋转 $45$ 度后的坐标。
所以:相似矩阵的目的是为了找到更简单的坐标系来描述变换。
建立不同的参考系,逆时针旋转 $45$ 度这个变换的矩阵都不一样,但是它们描述的是同一个线性变换,即本家兄弟,见面不认识,岂不成了笑
话。好在,我们可以找到同一个线性变换的矩阵兄弟们的一个性质,那就是:一定能找到一个非奇异矩阵 $P$,使得
$$P^{-1}AP = B$$
这个 $P$ 就是基 $(i_{1},j_{1})$ 到基 $(i_{2},j_{2})$ 的过渡矩阵,即
$$(i_{2},j_{2}) = (i_{1},j_{1}) cdot P$$
设向量 $alpha$ 在基 $i_{1},j_{1}$ 下的坐标为 $v_{1} = (x_{1},y_{1})^{T}$,在基 $i_{2},j_{2}$ 下的坐标为 $v_{2} = (x_{2},y_{2})^{T}$,于是
$$P cdot v_{2} = v_{1}$$
设逆时针旋转 $45$ 度在基 $i_{1},j_{1}$ 下的变换矩阵为 $A$,在基 $i_{2},j_{2}$ 下的变换矩阵为 $B$,基于两个参考系的坐标变换关系有
$$Av_{1} = PBv_{2}$$
由 $v_{1}$ 和 $v_{2}$ 的关系有
$$APv_{2} = PBv_{2}$$
故
$$P^{-1}AP = B$$