算法描述:
搜索时,只要尽可能,就在图中尽量深入。
深度优先搜索总是对最近才发现的结点v的出发边进行探索,直到该结点的所有出发边都被发现为止。一旦
结点v的所有出发边都被发现,探索则回溯到v的前驱结点,来探索该前驱结点的出发边。该过程一直持续到从
源节点可以到达的所有结点都被发现为止。
深度优先搜索树:
同广度优先搜索树一样,树中除根结点外的每个结点的父节点,为图中访问到该结点的前驱结点。
其前驱子图的数学定义为:
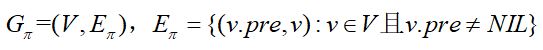
这里和广搜不同的是,深搜没有限定源结点的数量,所以其前驱子图可能是一个森林。
算法实现:
1.邻接矩阵法
int visited[N];
int edges[N][N];
void DFS(int start)
{
visited[start] = 1;
for(int i = 0; i < N; ++i)
{
if (edges[start][i] == 1 && visited[i] == 0)
{
DFS(i);
}
}
}
2. 邻接链表法
int visited[N];
vector<int> v[N];
void DFS(int start)
{
visited[start] = 1;
for(int i = 0; i < v[start].size(); ++i)
{
if (visited[i] == 0)
{
DFS(i);
}
}
}
邻接链表法时间复杂度分析:
使用聚合分析法进行分析,易知每个结点都会调用一次DFS(i),所以DFS(i)和visited[start] = 1这两行代码的代价为O(V)。
循环和判断操作的次数为所有的邻接边,故代价为O(E),所以总的时间复杂度为O(V+E)。