一:什么是卷积
离散卷积的数学公式可以表示为如下形式:
f(x) = - 其中C(k)代表卷积操作数,g(i)代表样本数据, f(x)代表输出结果。
举例如下:
假设g(i)是一个一维的函数,而且代表的样本数为G = [1,2,3,4,5,6,7,8,9]
假设C(k)是一个一维的卷积操作数, 操作数为C=[-1,0,1]
则输出结果f(x)可以表示为 F=[1,2,2,2,2,2,2,2,1] //边界数据未处理
以上只是一维的情况下,当对一幅二维数字图像加以卷积时,其数学意义可以解释如下:
源图像是作为输入源数据,处理以后要的图像是卷积输出结果,卷积操作数作为Filter
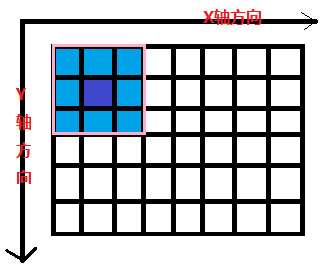
在XY两个方向上对源图像的每个像素点实施卷积操作。如图所示:
粉红色的方格每次在X/Y前进一个像素方格,就会产生一个新的输出像素,图中深蓝色的代
表要输出的像素方格,走完全部的像素方格,就得到了所有输出像素。
图中,粉红色的矩阵表示卷积操作数矩阵,黑色表示源图像– 每个方格代表一个像素点。
二:卷积在数字图像处理中应用
一副数字图像可以看作一个二维空间的离散函数可以表示为f(x, y), 假设有对于二维卷积操
作函数C(u, v) ,则会产生输出图像g(x, y) = f(x, y) *C(u,v), 利用卷积可以实现对图像模糊处理,边缘检测,产生轧花效果的图像。
一个简单的数字图像卷积处理流程可以如下:
1. 读取源图像像素
2. 应用卷积操作数矩阵产生目标图像
3. 对目标图像进行归一化处理
4. 处理边界像素
三使用模板处理图像相关概念:
模板:矩阵方块,其数学含义是一种卷积运算。
卷积运算:可看作是加权求和的过程,使用到的图像区域中的每个像素分别于卷积核(权矩阵)的每个元素对应相
乘,所有乘积之和作为区域中心像素的新值。
卷积核:卷积时使用到的权用一个矩阵表示,该矩阵与使用的图像区域大小相同,其行、列都是奇数,
是一个权矩阵。
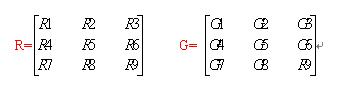
卷积示例:
3 * 3 的像素区域R与卷积核G的卷积运算:
R5(中心像素)=R1G1 + R2G2 + R3G3 + R4G4 + R5G5 + R6G6 + R7G7 + R8G8 + R9G9
四使用模板处理图像的问题:
边界问题:当处理图像边界像素时,卷积核与图像使用区域不能匹配,卷积核的中心与边界像素点对应,
卷积运算将出现问题。
处理办法:
A. 忽略边界像素,即处理后的图像将丢掉这些像素。
B. 保留原边界像素,即copy边界像素到处理后的图像。
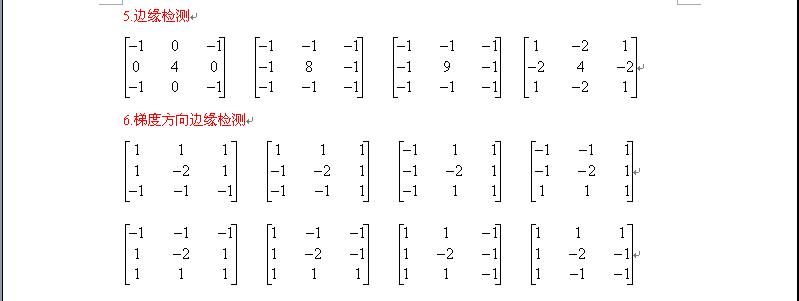
五.常用模板:
六其他
-----------------------------------------------------------------------------------------------------------
以下用$符号表示从负无穷大到正无穷大的积分。
一维卷积:
y(t)=g(k)*x(k)=$g(k)x(t-k)
先把函数x(k)相对于原点反折,然后向右移动距离t,然后两个函数相乘再积分,就得到了在t处的输出。对每个t值重复上述过程,就得到了输出曲线。
二维卷积:
h(x,y)=f(u,v)*g(u,v)=$$f(u,v)g(x-u,y-v)
先将g(u,v)绕其原点旋转180度,然后平移其原点,u轴上像上平移x, v轴上像上平移y。然后两个函数相乘积分,得到一个点处的输出。
在图像中卷积是什么意思呢,就是图像就是图像f(x),模板是g(x),然后将模版g(x)在模版中移动,每到一个位置,就把f(x)与g(x)的定义域相交的元素进行乘积并且求和,得出新的图像一点,就是被卷积后的图像.模版又称为卷积核.卷积核做一个矩阵的形状。由于大多数模板都是对称的,所以模板不旋转。
二维图像卷积运算
import numpy as np from scipy import signal from scipy import misc import matplotlib.pyplot as plt face=misc.face(gray=True) #创建一个灰度图像 scharr=np.array([[-3-3j,0-10j,+3-3j], [-10+0j,0+0j,+10+0j], [-3+3j,0+10j,+3+3j]]) #设置一个特殊的卷积和 grad=signal.convolve2d(face,scharr,boundary='symm',mode='same') #把图像的face数组和设计好的卷积和作二维卷积运算,设计边界处理方式为symm fig,(ax1,ax2)=plt.subplots(1,2,figsize=(10,6)) #建立1行2列的图fig ax1.imshow(face,cmap='gray') #显示原始的图 <matplotlib.image.AxesImage object at 0x00000000078FC198> ax1.set_axis_off() #不显示坐标轴 ax2.imshow(np.absolute(grad),cmap='gray') #显示卷积后的图 <matplotlib.image.AxesImage object at 0x00000000078FCE48> ax2.set_axis_off() #不显示坐标轴 fig.show() #显示绘制好的画布