最小二乘法多项式曲线拟合原理与实现 https://blog.csdn.net/jairuschan/article/details/7517773/
算法+OpenCV】基于opencv的直线和曲线拟合与绘制(最小二乘法) https://www.cnblogs.com/fengliu-/p/8031406.html



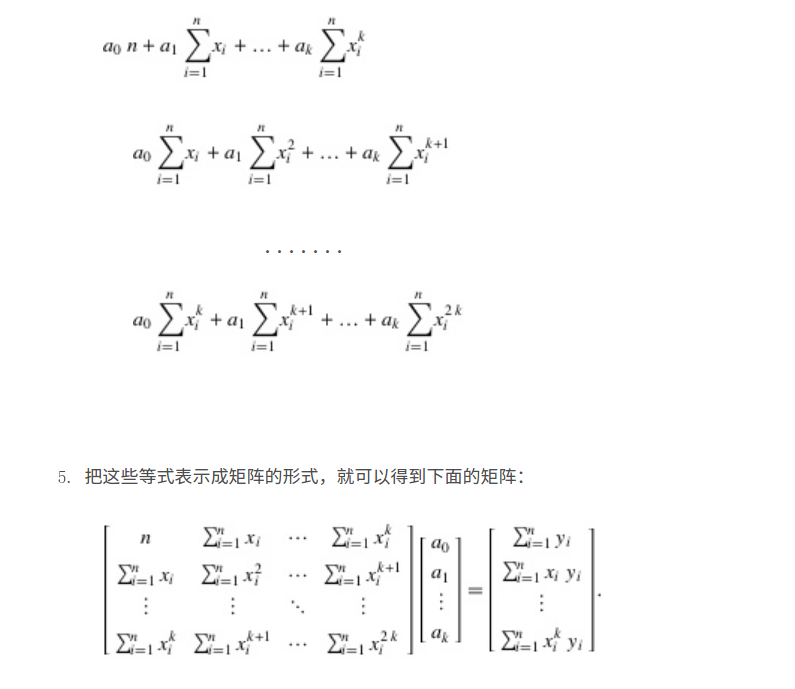

基于opencv c++代码如下:
#include <iostream>
#include <opencv.hpp>
#include<opencv2/opencv.hpp>
using namespace std;
using namespace cv;
void FitPolynomialCurve(const std::vector<cv::Point>& points, int n, cv::Mat& A){
//最小二乘法多项式曲线拟合原理与实现 https://blog.csdn.net/jairuschan/article/details/7517773/
//https://www.cnblogs.com/fengliu-/p/8031406.html
int N = points.size();
cv::Mat X = cv::Mat::zeros(n + 1, n + 1, CV_64FC1);
for (int i = 0; i < n + 1; i++){
for (int j = 0; j < n + 1; j++){
for (int k = 0; k < N; k++){
X.at<double>(i, j) = X.at<double>(i, j) +
std::pow(points[k].x, i + j);
}
}
}
cv::Mat Y = cv::Mat::zeros(n + 1, 1, CV_64FC1);
for (int i = 0; i < n + 1; i++){
for (int k = 0; k < N; k++){
Y.at<double>(i, 0) = Y.at<double>(i, 0) +
std::pow(points[k].x, i) * points[k].y;
}
}
A = cv::Mat::zeros(n + 1, 1, CV_64FC1);
cv::solve(X, Y, A, cv::DECOMP_LU);
}
int main(int argc, char **argv)
{
string path = "/data_1/everyday/1224/2.jpeg";
Mat img = imread(path);
Mat img_gray,img_bi;
cvtColor(img,img_gray,CV_BGR2GRAY);
threshold(img_gray,img_bi,80,255,THRESH_BINARY_INV);
vector<vector<Point> > contours;
vector<Vec4i> hierarchy;
findContours( img_bi, contours, hierarchy, CV_RETR_EXTERNAL, CV_CHAIN_APPROX_SIMPLE , Point(0, 0) );
std::cout<<contours[0].size()<<std::endl;
cv::Mat img_draw = cv::Mat(img.rows,img.cols,CV_8UC3,Scalar(0,0,255));
drawContours(img_draw,contours,-1,Scalar(255,255,255));
int n = 3;
cv::Mat A;
FitPolynomialCurve(contours[0], n, A);
std::vector<cv::Point> points_fitted;
for (int x = 0; x < 800; x++)
{
double y = A.at<double>(0, 0) + A.at<double>(1, 0) * x +
A.at<double>(2, 0)*std::pow(x, 2) + A.at<double>(3, 0)*std::pow(x, 3);
points_fitted.push_back(cv::Point(x, y));
}
cv::polylines(img_draw, points_fitted, false, cv::Scalar(0, 0, 0), 1, 8, 0);
imshow("img_src",img);
imshow("img_draw",img_draw);
imshow("img_bi",img_bi);
waitKey(0);
return 0;
}
效果图如下:

但是我后面又整了个S形状的图像,找不到能够很好拟合的函数阶数。
#include <iostream>
#include <opencv.hpp>
#include<opencv2/opencv.hpp>
using namespace std;
using namespace cv;
void FitPolynomialCurve(const std::vector<cv::Point>& points, int n, cv::Mat& A){
//最小二乘法多项式曲线拟合原理与实现 https://blog.csdn.net/jairuschan/article/details/7517773/
//https://www.cnblogs.com/fengliu-/p/8031406.html
int N = points.size();
cv::Mat X = cv::Mat::zeros(n + 1, n + 1, CV_64FC1);
for (int i = 0; i < n + 1; i++){
for (int j = 0; j < n + 1; j++){
for (int k = 0; k < N; k++){
X.at<double>(i, j) = X.at<double>(i, j) +
std::pow(points[k].x, i + j);
}
}
}
cv::Mat Y = cv::Mat::zeros(n + 1, 1, CV_64FC1);
for (int i = 0; i < n + 1; i++){
for (int k = 0; k < N; k++){
Y.at<double>(i, 0) = Y.at<double>(i, 0) +
std::pow(points[k].x, i) * points[k].y;
}
}
A = cv::Mat::zeros(n + 1, 1, CV_64FC1);
cv::solve(X, Y, A, cv::DECOMP_LU);
}
int main(int argc, char **argv)
{
string path = "/data_1/everyday/1224/3.jpeg";
Mat img = imread(path);
Mat img_gray,img_bi;
cvtColor(img,img_gray,CV_BGR2GRAY);
threshold(img_gray,img_bi,80,255,THRESH_BINARY_INV);
vector<vector<Point> > contours;
vector<Vec4i> hierarchy;
findContours( img_bi, contours, hierarchy, CV_RETR_EXTERNAL, CV_CHAIN_APPROX_SIMPLE , Point(0, 0) );
std::cout<<contours[0].size()<<std::endl;
cv::Mat img_draw = cv::Mat(img.rows,img.cols,CV_8UC3,Scalar(0,0,255));
drawContours(img_draw,contours,-1,Scalar(255,255,255));
int n = 9;
cv::Mat A;
FitPolynomialCurve(contours[0], n, A);
std::vector<cv::Point> points_fitted;
for (int x = 0; x < 800; x++)
{
double y = A.at<double>(0, 0) + A.at<double>(1, 0) * x +
A.at<double>(2, 0)*std::pow(x, 2) + A.at<double>(3, 0)*std::pow(x, 3) + A.at<double>(4, 0)*std::pow(x, 4) + A.at<double>(5, 0)*std::pow(x, 5)
+ A.at<double>(6, 0)*std::pow(x, 6) + A.at<double>(7, 0)*std::pow(x, 7) + A.at<double>(8, 0)*std::pow(x, 8) + A.at<double>(9, 0)*std::pow(x, 9);
//+ A.at<double>(10, 0)*std::pow(x, 10) + A.at<double>(11, 0)*std::pow(x, 11) + A.at<double>(12, 0)*std::pow(x, 12);
points_fitted.push_back(cv::Point(x, y));
}
cv::polylines(img_draw, points_fitted, false, cv::Scalar(0, 0, 0), 1, 8, 0);
imshow("img_src",img);
imshow("img_draw",img_draw);
imshow("img_bi",img_bi);
waitKey(0);
return 0;
}

突然想明白,这个S形状曲线一个x对应好几个y,不行。需要一个x唯一对应一个y的曲线才能拟合。然后又顺手画了一个,果真可以拟合。

当然代码每次根据不同的阶数写好多A.at
double CurveY(double x, cv::Mat& A){
double y = 0.0;
double *a = A.ptr<double>();
for (int i = 0; i < A.rows; i++){
y += a[i] * pow(x, i);
}
return y;
}