编程作业2.2：Regularized Logistic regression

题目

在本部分的练习中，您将使用正则化的Logistic回归模型来预测一个制造工厂的微芯片是否通过质量保证（QA），在QA过程中，每个芯片都会经过各种测试来保证它可以正常运行。假设你是这个工厂的产品经理，你拥有一些芯片在两个不同测试下的测试结果，从这两个测试，你希望确定这些芯片是被接受还是拒绝，为了帮助你做这个决定，你有一些以前芯片的测试结果数据集，从中你可以建一个Logistic回归模型。

编程实现

在这部分训练中，我们将要通过加入正则项提升逻辑回归算法。简而言之，正则化是成本函数中的一个术语，它使算法更倾向于“更简单”的模型（在这种情况下，模型将更小的系数）。这个理论助于减少过拟合，提高模型的泛化能力。

1.Visualizing the data

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

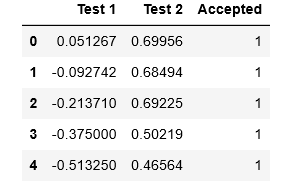
data2 = pd.read_csv('D:BaiduNetdiskDownloaddata_setsex2data2.txt', names=['Test 1', 'Test 2', 'Accepted'])
data2.head()

def plot_data():
    
    # 把数据分成 positive 和 negetive 两类
    positive = data2[data2['Accepted'].isin([1])]
    negative = data2[data2['Accepted'].isin([0])]
    
    fig, ax = plt.subplots(figsize=(8,5))
    ax.scatter(positive['Test 1'], positive['Test 2'], s=50, c='b', marker='o', label='Accepted')
    ax.scatter(negative['Test 1'], negative['Test 2'], s=50, c='r', marker='x', label='Rejected')
    ax.legend(loc=2)
    ax.set_xlabel('Test 1 Score')
    ax.set_ylabel('Test 2 Score')
    
plot_data()

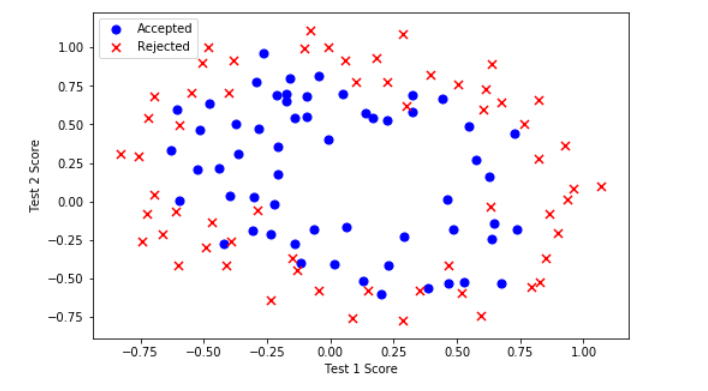
注意到其中的正负两类数据并没有线性的决策界限。因此直接用logistic回归在这个数据集上并不能表现良好，因为直接用logistic回归只能用来寻找一个线性的决策边界。
所以接下会提到一个新的方法。

2.Feature mapping

一个拟合数据的更好的方法是从每个数据点创建更多的特征。

我们将把这些特征映射到所有的x1和x2的多项式项上，直到第六次幂。

# 特征映射函数
def feature_mapping(x1, x2, power):
    data = {}
    for i in np.arange(power + 1): # for(i=0,i<power+1,i++)
        for p in np.arange(i + 1): # for(p=0,p<i+1,p++)
            data["f{}{}".format(i - p, p)] = np.power(x1, i - p) * np.power(x2, p) # f{i-p}{p} = x1^(i-p) * x2^(p)

#      data = {"f{}{}".format(i - p, p): np.power(x1, i - p) * np.power(x2, p)
#                 for i in np.arange(power + 1)
#                 for p in np.arange(i + 1)
#             }
    return pd.DataFrame(data)


x1 = data2['Test 1'].values
x2 = data2['Test 2'].values

# 把特征映射到power=6
_data2 = feature_mapping(x1, x2, power=6)
_data2.head()

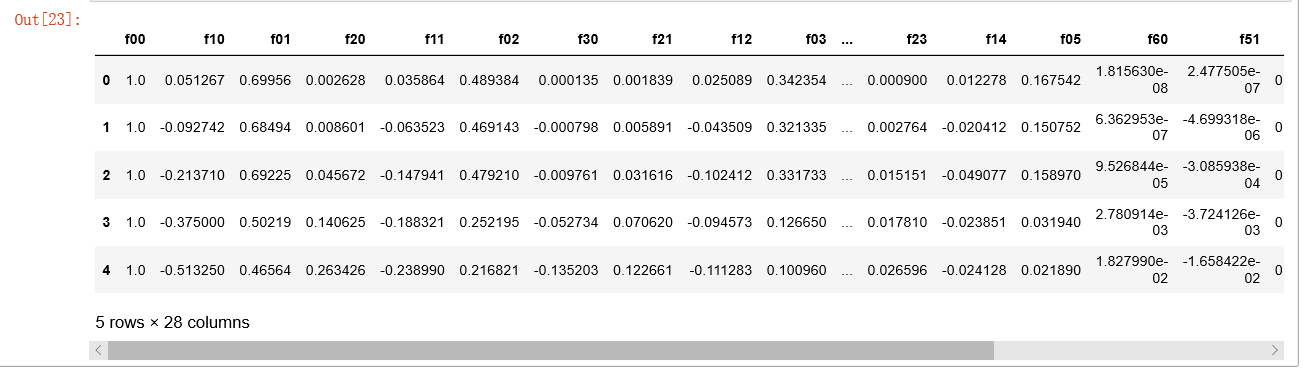
经过映射，我们将有两个特征的向量转化成了一个28维的向量。
在这个高维特征向量上训练的logistic回归分类器将会有一个更复杂的决策边界，当我们在二维图中绘制时，会出现非线性。
虽然特征映射允许我们构建一个更有表现力的分类器，但它也更容易过拟合。

在接下来的练习中，我们将实现正则化的logistic回归来拟合数据，并且可以看到正则化如何帮助解决过拟合的问题。

3.Regularized Cost function

正则化逻辑回归的代价函数如下：

[J( heta)=frac1m sum_{i=1}^m left( - y^{left(i ight)} log left( h_ heta left( x^{left( i ight)} ight) ight) - left( 1-y^{left( i ight)} ight) log left( 1- h_ heta left( x^{left( i ight)} ight) ight) ight) + frac {lambda}{2m} sum_{j=1}^n heta_j^2 ]

注意： 不惩罚第一项( heta_0)

先获取特征，标签以及参数theta，确保维度良好：

# 这里因为做特征映射的时候已经添加了偏置项，所以不用手动添加了。
X = _data2.values 
y = data2['Accepted'].values
theta = np.zeros(X.shape[1]) # X.shape[1]获取X的列数，这里theta是列向量
X.shape, y.shape, theta.shape 

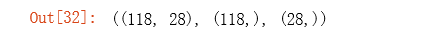
def sigmoid(z):
    return 1 / (1 + np.exp(- z))

# 定义代价函数（能够返回代价函数值）
def cost(theta, X, y):
    first = (-y) * np.log(sigmoid(X @ theta)) # 注意这里的 theta 是列向量
    second = (1 - y)*np.log(1 - sigmoid(X @ theta))
    return np.mean(first - second)

# 定义带正则项的代价函数
def costReg(theta, X, y, l=1):
    # 不惩罚第一项
    _theta = theta[1: ] #选取第二项以后的； _theta为27*1的向量；theta[1: ]是列向量
    
    # theta@_theta：这个numpy一维数组的特殊用法，也就相当于求内积，也就是元素平方的和。
    # @在numpy中表示矩阵相乘的意思，等价于np.dot()
    reg = (l / (2 * len(X))) *( (_theta).T @ _theta)  # _theta@_theta == inner product（点积，结果是一个数）；这里用_theta@_theta 和(_theta).T @ _theta是一样的
    
    return cost(theta, X, y) + reg

计算正则化代价函数的初始值：

# 计算正则化代价函数的初始值：
costReg(theta, X, y, l=1)  

4.Regularized gradient

因为我们未对({ heta }_{0})进行正则化，所以梯度下降算法将分两种情形：

[frac{partial }{partial heta_0} J( heta)=frac1m sum_{i=1}^m left( h_ heta left( x^{ left(i ight) } ight) -y^{ left(i ight) } ight) x_{0}^{left(i ight)} ]

[frac{partial }{partial heta_j} J( heta)=frac1m sum_{i=1}^m left( h_ heta left( x^{ left(i ight) } ight) -y^{ left(i ight) } ight) x_{j}^{left(i ight)} + frac lambda m heta_j，其中j=1,2,cdots,n ]

# 定义计算梯度值（导数值）
def gradient(theta, X, y):
    return (X.T @ (sigmoid(X @ theta) - y))/len(X)  
# the gradient of the cost is a vector of the same length as θ where the jth element (for j = 0, 1, . . . , n)

# 定义正则化梯度值（导数值）
def gradientReg(theta, X, y, l=1):
    reg = (l / len(X)) * theta
    reg[0] = 0  # 不惩罚第一项
    return gradient(theta, X, y) + reg

gradientReg(theta, X, y, 1)

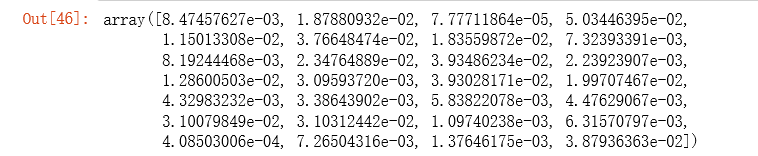
5.Learning θ parameters

import scipy.optimize as opt

# 这里使用fimin_tnc方法来拟合
# func：优化的目标函数
# x0：初值
# fprime：提供优化函数func的梯度函数，不然优化函数func必须返回函数值和梯度，或者设置approx_grad=True
# args：元组，是传递给优化函数的参数
result2 = opt.fmin_tnc(func=costReg, x0=theta, fprime=gradientReg, args=(X, y, 1))
result2

计算经过高级优化算法之后正则化代价函数的值：

# result2[0] 是优化过后的参数值
costReg(result2[0], X, y, l=1)

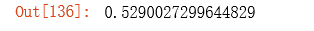
6.Evaluating logistic regression

def predict(theta, X):
    probability = sigmoid(X @ theta)
    return [1 if x >= 0.5 else 0 for x in probability]  # return a list


final_theta = result2[0]
predictions = predict(final_theta, X)
correct = [1 if a==b else 0 for (a, b) in zip(predictions, y)]
accuracy = sum(correct) / len(correct)
accuracy

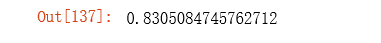
可以看到预测精度达到了83%。

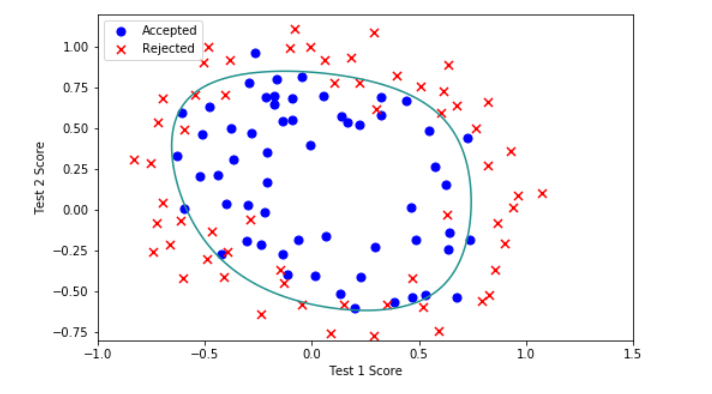
7.Decision boundary

x = np.linspace(-1, 1.5, 250)
xx, yy = np.meshgrid(x, x)

z = feature_mapping(xx.ravel(), yy.ravel(), 6).values
z = z @ final_theta
z = z.reshape(xx.shape)

plot_data()
plt.contour(xx, yy, z, 0)
plt.ylim(-.8, 1.2)

总结

当我们选取非常多的特征来拟合数据（本练习最终映射了28个特征）的时候，很容易出现过拟合的现象（即对训练集的数据拟合的非常好，但是泛化新样本的能力却不太好），这时候就需要进行正则化。(lambda)是正则化参数，它的作用是可以更好的拟合数据集，保持参数尽量地小，从而保持假设函数模型相对简单，避免出现过拟合的现象。

(lambda)值的选取也很重要，当(lambda)过大时，容易出现欠拟合，偏差大的情况，当(lambda)的值太小，容易出现过拟合，方差大的情况。

• (lambda=0)
  
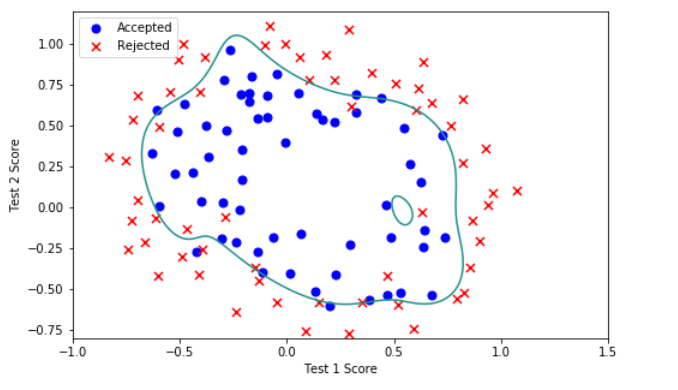
• (lambda=1)
  
• (lambda=10)
  
• (lambda=100)
  

对比以上(lambda)取0、1、10、100的情况，某种程度上说，(lambda=1)是比较合适的。所以正则化中(lambda)值的选取非常重要。

参考资料

什么是多项式的特征映射？

Scipy优化算法--scipy.optimize.fmin_tnc()/minimize()