normal equation(正规方程)
- 正规方程是通过求解下面的方程来找出使得代价函数最小的参数的:
[frac{partial}{partial heta_j}Jleft( heta
ight)=0
]
- 假设我们的训练集特征矩阵为 (X)(包含了(x_0=1))并且我们的训练集结果为向量 (y),则利用正规方程解出向量:
[ heta ={{left( {X^T} X
ight)}^{-1}}{X^T}y
]
- 梯度下降与正规方程的比较:
- 梯度下降:需要选择学习率(alpha);需要多次迭代;当特征数量n大时也能较好适用,适用于各种类型的模型;
- 正规方程:不需要选择学习率(alpha);不需要迭代,一次运算就可以得出( heta)的最优解;需要计算({left( {X^T} X ight)}^{-1});如果特征数量n较大则运算代价大,因为矩阵逆的计算时间复杂度为(O(n^3)),通常来说当n小于10000时还是可以接受的,只适用于线性模型,不适合逻辑回归模型等其他模型。
编程实现
在编程作业1.1:单变量线性回归的基础上实现:
# 正规方程
def normalEqn(X, y):
theta = np.linalg.inv(X.T@X)@X.T@y #X.T@X等价于X.T.dot(X);np.linalg.inv():矩阵求逆
return theta
final_theta2=normalEqn(X, y)#感觉和批量梯度下降的theta的值有点差距
final_theta2
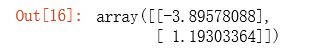
在之前运行完梯度下降算法之后,我们输出( heta)的值如下:

可以看出两种方法求出的( heta)值基本相似。