在弄清楚InfoGAN之前,可以先理解一下变分推断目的以及在概率论中的应用与ELBO是什么,以及KL散度 https://blog.csdn.net/qy20115549/article/details/93074519
https://blog.csdn.net/qy20115549/article/details/86644192。
如果理解了变分推断,KL散度,ELBO,对于InfoGAN中的重要方法就可以很容易理解了。
这里首先看一下简单的对数推导为方便对InfoGAN文中的公式的阅读:
![]()
下面的笔记参阅:
https://blog.csdn.net/u011699990/article/details/71599067
https://www.cnblogs.com/zzycv/p/9312039.html
先记一下预备知识就当作复习了。
条件熵公式推导:
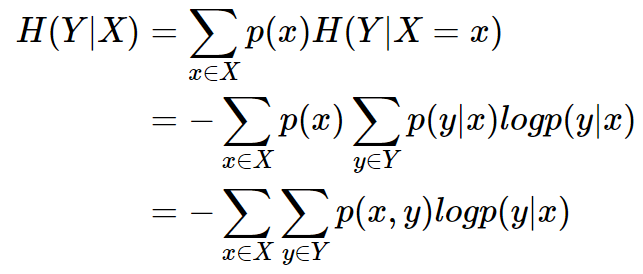
用另一个变量对原变量分类后, 原变量的不确定性就会减小, 不确定程度减小了就是信息增益。
互信息(Mutual Information, MI)是变量间相互依赖性的度量, 它度量两个事件集合之间的相关性。
两个离散随机变量X和Y的互信息可定义为:
![]()
p(x,y)是X和Y的联合概率分布函数, 而p(x)和p(y)分别是X和Y的边缘概率分布函数
在连续随机变量的情形下:
![]()
I(X;Y)的一些计算:

GAN
总的来说,这个生成模型就是通过两个神经网络互相之间的竞争对抗来进行训练。这两个网络中有一个是生成器,它需要将随机的噪声分布z映射到我们需要得到的真实分布x,另外一个网络就是判别器,从真实数据和生成的数据中间随机采样,判断这个数据是否是真实数据,在这里判别器D相当于一个二分类器。所以,整个优化问题就转换为一个minmax game,D(x)代表x来自真实数据的概率,在训练过程中,最大化D(x)的值,同时,最小化生成器生成数据的能力,从而达到两个网络互相竞争,互相进步,生成器生成数据的能力越来越强,判别器判别数据的能力也越来越强。

如果从表征学习的角度来看GAN模型,会发现,由于在生成器使用噪声z的时候没有加任何的限制,所以在以一种高度混合的方式使用z,z的任何一个维度都没有明显的表示一个特征,所以在数据生成过程中,我们无法得知什么样的噪声z可以用来生成数字1,什么样的噪声z可以用来生成数字3,我们对这些一无所知,这从一点程度上限制了我们对GAN的使用。

InfoGAN
基于上面的分析,作者就在生成器中除了原先的噪声z还增加了一个隐含编码c,提出了一个新的GAN模型—InfoGAN,其中Info代表互信息,它表示生成数据x与隐藏编码c之间关联程度的大小,为了使得x与c之间关联密切,所以我们需要最大化互信息的值,据此对原始GAN模型的值函数做了一点修改,相当于加了一个互信息的正则化项。是一个超参,通过之后的实验选择了一个最优值1。

上面的I(C|X)中的|应该为";" 即I(C;X), I(C;X=G(Z,C))

在实践的过程中, 发现在计算互信息的值时, 需要用到后验分布(P(C|X),但是这是一个很难采样和估计的一个值。作者想出通过定义一个辅助分布来协助估计后验分布。这就与文中第一次给出的简单的对数推导连上了。

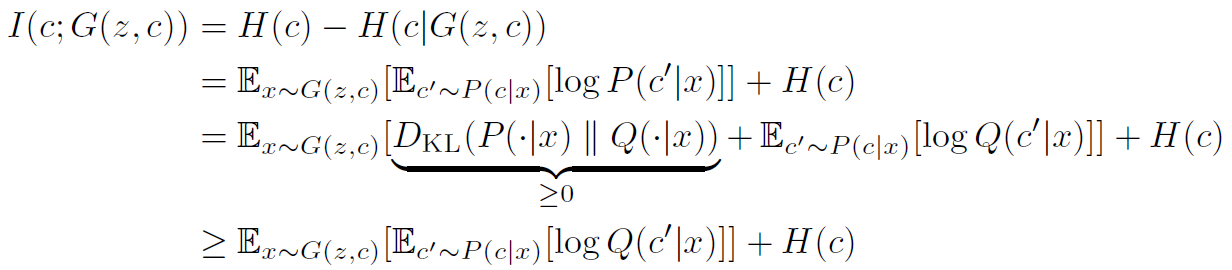
在引入辅助分布之后,通过变分分布最大化来最大化这个互信息的下界,这里是整个推导过程。


使用Q来接近p得到了互信息的变分估计, 在论文中提到, 为了优化方便, 作者固定了隐编码的分布, 因此H(C)是一个常量.通过对G,Q的优化来最大化L(G,Q),当时,不等式取等号,从而得到最大化互信息的效果。所以InfoGAN的最优化问题中的互信息正则项替换为L(G,Q)。但是在L(G,Q)中发现,还是有个后验分布。 作者利用一个定理来消除这个后验分布, 如下:
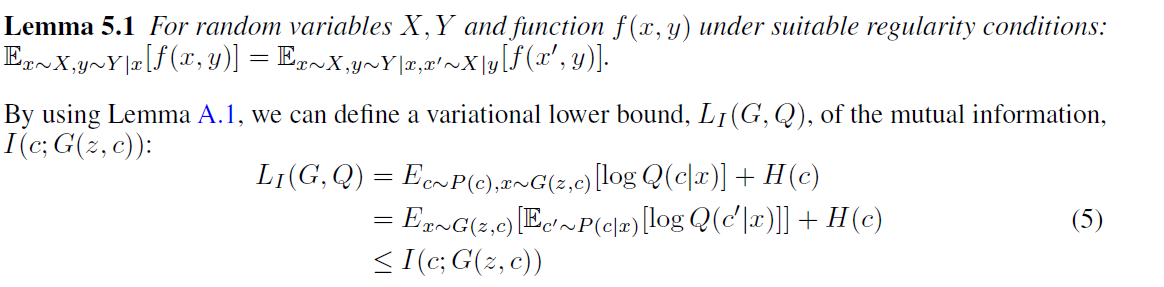
更详细的推导如下:

定理的证明:

因此就可以得到最小最大值InfoGAN,V(D,G)减去超参数λ与互信息变分正则化项的乘积,
![]()
在InfoGAN模型中,GAN的网络结构用的是DCGAN。给生成器输入隐含编码c和噪声z,生成假的数据,从假数据和真实数据中随机采样,输入给定D进行判断,是真还是假。Q通过与D共享卷积层,可以减少计算花销。在这里,Q是一个变分分布,在神经网络中直接最大化,Q也可以视作一个判别器,输出类别c。

实验,主要有两个目标,第一个是验证互信息可以被有效的最大化,第二个是验证InfoGAN是否可以学到可分解的可解释的特征。在第一个实验中,使用MNIST数据集,隐含编码c设为包括10个类别的离散编码,均匀分布,并使用GAN中同样加了一个辅助分布Q做对比试验。实验中发现,InfoGAN中L可以很快收敛到H(c),而GAN中,生成的图片与隐含编码c之间的互信息几乎没有,说明GAN中并没有用到这个隐含编码。

第二个实验来尝试学习数据集中可分解的特征。同样的使用MNIST数据集,在这里使用了三个隐含编码,c1用十个离散数字进行编码,每个类别的概率都是0.1,c2,c3连续编码,是-2到2的均匀分布。通过实验发现,c1可以作为一个分类器,分类的错误率为5%,图片a中第二行将7识别为9,但是不是意味着c1的0-9分别代表着生成数字的0-9,这是为了可视化效果,对数据重新排序的结果。如果在常规的GAN模型中添加c1编码,发现生成的图片与c1没有明显的关联。通过观察发现,c2表示生成数字的旋转的角度,c3表示生成数字的宽度。图c显示,小的c2值表示数字向左偏,大的c2值表示数字向右偏。图d显示,c3的值越大,生成的数字越宽。

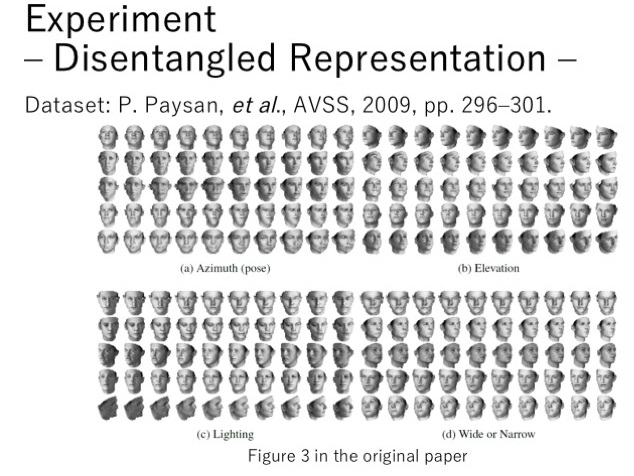
除了MNIST数据集外,还在其他数据集上做了实验。比如在一个3D的人脸数据集中,使用多个连续的编码,得到了一些不同的特征。比如图a中,可以得到人脸转向的特征,图b得到了人脸仰角大小的特征,图c得到了图片亮度的特征,图d得到人脸宽窄的特征。
在3d椅子的数据集中,图a表示可以得到不同椅子旋转角度不同的特征,图b表示可以得到不同椅子宽度不同的特征。

在一个街景的楼栋数字数据集中,也得到了不同的特征。如图a所示,可以获取这些数字图片不同的亮度,图b所示,可以区分出图片中不同的数字。

在CelebA数据集中,同样的可以通过不同的编码获取一些特征,比如人脸不同的转向角度,是否带了眼镜,发型的不同,情绪的变化。

最后提出了一些未来工作的设想,将互信息最大化应用到其他的方法,尝试学习层级特征,用来提高半监督学习,发现更高维度的数据。通过这篇paper当中的实验发现,隐含编码c学习到的内容很丰富,可以用来进行半监督学习的分类。(往真实数据中添加噪声,可以使训练更稳定)