Numpy的介绍
1. Ndarray:N-dimensional array, N维数组
2. 一种由相同类型的元素组成的多维数组,元素数量是事先指定好的
例:建立Ndarray多维数组 ndarray父类实现矩阵的创建基本方式:
arr = np.array(
[
[1,2,3,4],
[2,3,4,5]
])
这是一个二维数组arr.ndim为2 这个数组的形状arr.shape为(2, 4)即2行4列
这个数组的元素个数np.size为8个,这个数组的数据类型arr.dtype为int32
shape属性-->几行几列
ndim属性-->几维度 向量-->1维度 矩阵-->二维度 数组-->3维度
size属性-->数组元素的个数
dtype-->元素类型
1 # 矩阵的定义 2 import numpy as np 3 b = np.array([[1,2,3,4], [2,3,4,5]]) 4 print(b) 5 print(type(b)) 6 7 # 矩阵的性质几行几列 8 print('shape',b.shape) # (2,4) 9 # 几维度 向量-->1维度 矩阵-->二维度 数组-->3维度 10 print(b.ndim) # 2 11 # 元素类型 12 print(b.dtype) # int32 13 # 数组元素的个数 14 print(b.size) # 8 => 2*4
3. 元素的数据类型由dtype(data-type)对象来指定,每个ndarray只有一种dtype类型
例:
np.array(['Python','cctv','ibeifeng','hello world'],dtype='|S4')
输出结果array([b'Pyth', b'cctv', b'ibei', b'hell'], dtype='|S4')
其中S4中的S表示字符串型,4表示每个字符串长度为4,所以输出结果每个数组只有4个字符
arr3 = np.array(['1','2','3','4'],dtype='int') # 表明arr3为整型
# 输出array([1, 2, 3, 4])
arr3 = np.array(['1','2','3','4'],dtype='float') # 表明arr3为浮点型
# 输出array([1., 2., 3., 4.])
4. 大小固定,创建好数组时一旦指定好大小,就不会再发生改变
数组的形状可以方便的读取数字例如
arr1 = np.array([[[ 1, 2, 3, 4, 5],
[ 2, 3, 4, 5, 6],
[ 3, 7, 4, 5, 6],
[ 3, 1, 4, 6, 7]],
[[11, 2, 23, 54, 5],
[28, 32, 42, 53, 46],
[35, 27, 74, 55, 86],
[63, 61, 44, 64, 87]]])
这个数组的形状为(2,4,5)可以通过arr1[0][1][1]这个形式取到3
ndarray的常见创建方式
- array函数:接收一个普通的Python序列,转成ndarray
- zeros函数:创建指定长度或形状的全零数组
np.zeros((3,4)) 创建3行4列全为0的数组,且默认为float型
3. ones函数:创建指定长度或形状的全1数组
np.ones((3,4),dtype=int) 创建3行4列全为1的整形数组,如果没有dtype=int,默认为float型
4. empty函数:创建一个没有任何具体值的数组(准确地说是一些未初始化的垃圾值)
np.empty((7,4)) 创建7行4列随机值数组,float型
ndarray的其他创建方式
1.arrange函数:类似与python的range函数,通过指定开始值、终值和步长来创建一维数组,注意数组不包括终值
np.arange(2,20,3)
# 输出 array([ 2, 5, 8, 11, 14, 17])
2. linspace函数:通过指定开始值、终值和元素个数来创建一维数组,可以通过endpoint关键字指定是否包括终值,缺省设置是包括终值,它创建的是等差数列
np.linspace(2,20,3) 包含20
# 输出 array([ 2., 11., 20.])
3.logspace函数:和linspace类似,但它创建的是等比数列
np.logspace(2,20,3)
# 输出 array([1.e+02, 1.e+11, 1.e+20])
4.使用随机数填充数组,即使用numpy.random模块的random()函数,数组所包含的元素数量由参数决定
np.random.random((2,3,4))
# 输出 array([[[0.40595225, 0.80061568, 0.16821289, 0.05557114],
[0.96146758, 0.81135374, 0.93132755, 0.11023897],
[0.79526355, 0.61563423, 0.78924163, 0.21849418]],
[[0.36029206, 0.883596 , 0.60343721, 0.38746385],
[0.92802328, 0.91256992, 0.61305594, 0.86444498],
[0.6619579 , 0.55846171, 0.37563522, 0.35721423]]])
np.random.random_sample()生成一位随机数
ndarry的shape属性巧算
np.arange(2,20,2).reshape((3,-1)) # -1 则会自动计算维度
# 输出 array([[ 2, 4, 6],
[ 8, 10, 12],
[14, 16, 18]])
总结:
- 先规范显示出数组
- 层层去中括号对,直到无中括号对,每去一层,一个维度,去掉一层[],后的元素个数(逗号隔开)即该维度的元素个数
NumPy中的数据类型
1. 创建NumPy数组时可以通过dtype属性显示指定数据类型,如果不指定,NumPy会自己推断出合适的数据类型,所以一般无需显示指定
arr2=np.arange(2,10,2),无需指定可判断为int32型
2. astype方法,可以转换数组的元素数据类型,得到一个新数组
arr3 = arr2.astype('float') # 为float64型
# 输出array([2., 4., 6., 8.])
arr4 = arr2.astype('|U2') # 使用unicode编码,每个元素长度为2
# 输出array(['2', '4', '6', '8'], dtype='<U2')
3.数值型dtype的命名方式:一个类型名(比如int、float),后面接着一个用于表示各元素位长的数字
比如表中的双精度浮点值,即Python中的float对象,需要占用8个字节(即64位),因此该类型在NumPy中就记为float64
4.每种类型有一个相对应的类型代码,即简写方式,参照下面的表
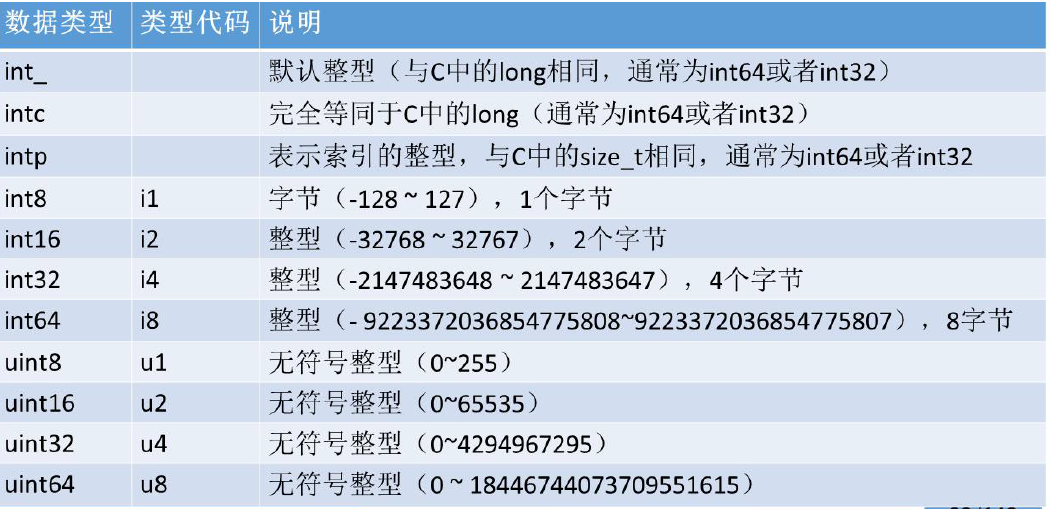
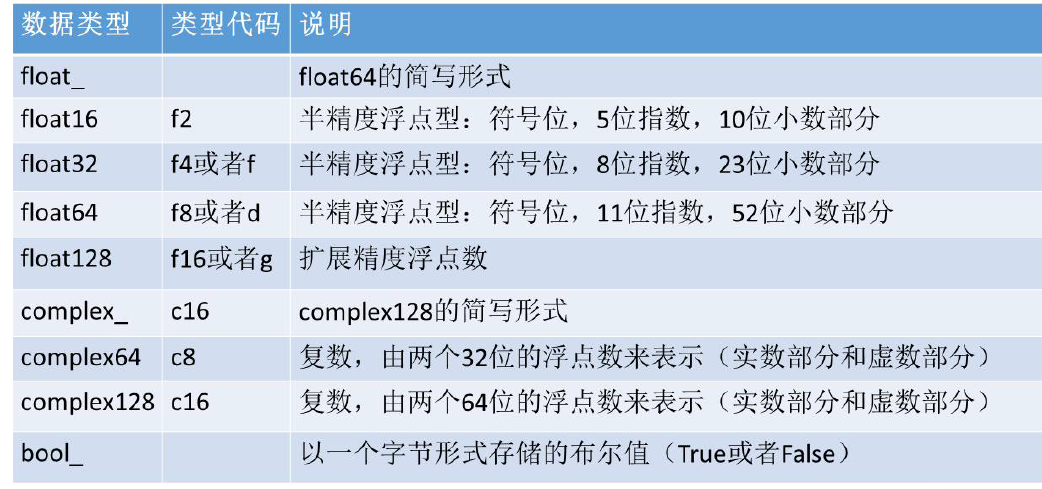

改变ndarray的形状
1. 直接修改ndarray的shape值
2. 使用reshape函数,可以创建一个改变了尺寸的新数组,原数组的shape保持不变,但注意他们共享内存空间,
因此修改任何一个也对另一个产生影响,因此注意新数组的元素个数必须与原数组一样
arr=np.arange(20)
arr.reshape((4,5))
# 输出array([[ 0, 1, 2, 3, 4],
[ 5, 6, 7, 8, 9],
[10, 11, 12, 13, 14],
[15, 16, 17, 18, 19]])
reshape函数不会改变原来的ndarray,但是得到的新的ndarray是原数组的视图
视图
多个变量使用(指向)一个内存地址(空间)
对于ndarray的一些方法操作,首先区分是否会改变原变量,以此来判断是视图还是副本
副本
把原来的内容,重新复制(拷贝)了一份新的数据,放到新的内存地址(空间)
即使修改了其中一个变量的元素值,并不会影响另外一个变量
3. 当指定新数组某个轴的元素为-1时,将根据数组元素的个数自动计算此轴的长度
arr2=arr.reshape((2,-1))
# array([[ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9],
[10, 11, 12, 13, 14, 15, 16, 17, 18, 19]])
NumPy基本操作
- 数组与标量、数组之间的运算
- 数组的矩阵积(matrix product)
- 数组的索引与切片
- 数组转置与轴对换
- 通用函数:快速的元素级数组函数
- 聚合函数
- np.where函数
- np.unique函数
数组与标量、数组之间的运算
- 数组不用循环即可对每个元素执行批量运算,这通常就叫做矢量化,即用数组表达式代替循环的做法
- 矢量化数组运算性能要比纯Python方式快上一两个数量级
- 大小相等的数组之间的任何算数运算都会将运算应用到元素级
元素级运算
- 像上面例子展现出来的,加、减、乘、除、幂运算等,可以用于数组与标量、大小相等数组之间
- 在NumPy中,大小相等的数组之间运算,为元素级运算,即只用于位置相同的元素之间,所得到的运算结果组成一个新的数组,运算结果的位置跟操作数位置相同
arr1=np.random.random((2,3))
arr2=np.arange(1,7).reshape(2,3) #arr2必须转换为2行3列才能和arr1进行加、减、
乘、除、幂运算
数组的矩阵积(matrix product)
1. 两个二维矩阵(多维数组即矩阵)满足第一个矩阵的列数与第二个矩阵的行数相同,那么可以进行矩阵乘法,即矩阵积不是元素级的运算
因为矩阵积是第一个矩阵的行与第二个矩阵的列相乘
f
a,b,c . g = a*f+b*g+c*h
(行) h
(列)
注意:矩阵积:第一个矩阵的列轴(水平的轴)要等于第二个矩阵的行轴(垂直的轴)
- 两个矩阵相乘结果所得到的数组中每个元素为,第一个矩阵中与该元素行号相同的元素与第二个矩阵中与该元素列号相同的元素,两两相乘后求和