数据标准化方法及其Python代码实现

 

数据的标准化(normalization)是将数据按比例缩放，使之落入一个小的特定区间。目前数据标准化方法有多种，归结起来可以分为直线型方法(如极值法、标准差法)、折线型方法(如三折线法)、曲线型方法(如半正态性分布)。不同的标准化方法，对系统的评价结果会产生不同的影响，然而不幸的是，在数据标准化方法的选择上，还没有通用的法则可以遵循。

常见的方法有：min-max标准化（Min-max normalization），log函数转换，atan函数转换，z-score标准化（zero-mena normalization，此方法最为常用），模糊量化法，均值归一化。本文只介绍min-max标准化、Z-score标准化方法、均值归一化、log函数转换、atan函数转换。

data = [1, 3, 4, 5, 2, 13, 23, 71, 11, 19, 9, 24, 38]

一、min-max标准化（Min-Max Normalization）

也称为离差标准化，是对原始数据的线性变换，使结果值映射到[0 - 1]之间。转换函数如下：

from __future__ import print_function, division


# min-max标准化方法
data0 = [(x - min(data))/(max(data) - min(data)) for x in data]

二、Z-score标准化方法

这种方法给予原始数据的均值（mean）和标准差（standard deviation）进行数据的标准化。经过处理的数据符合标准正态分布，即均值为0，标准差为1，转化函数为：

from __future__ import print_function
import math


# 均值
average = float(sum(data))/len(data)


# 方差
total = 0
for value in data:
    total += (value - average) ** 2
 
stddev = math.sqrt(total/len(data))


# z-score标准化方法
data1 = [(x-average)/stddev for x in data]

三、均值归一化

两种方式，以max为分母的归一化方法和以max-min为分母的归一化方法

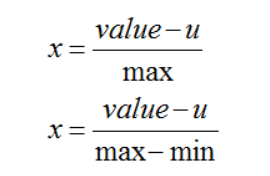
from __future__ import print_function

# 均值
average = float(sum(data))/len(data)


# 均值归一化方法
data2_1 = [(x - average )/max(data) for x in data]

data2_2 = [(x - average )/(max(data) - min(data)) for x in data]

 四、log函数转换方法

from __future__ import print_function

import math


# log2函数转换
data3_1 = [math.log2(x) for x in data]


# log10函数转换
data3_2 = [math.log10(x) for x in data]

 五、atan函数转换方法

from __future__ import print_function

import math


# atan函数转换方法
data4 = [math.atan(x) for x in data]