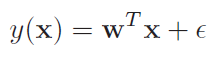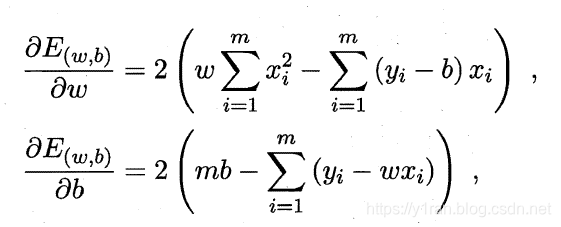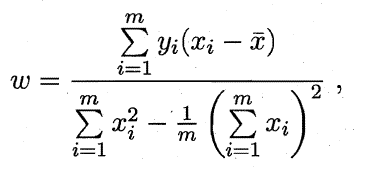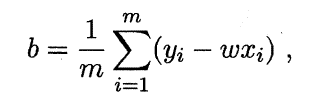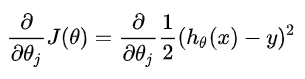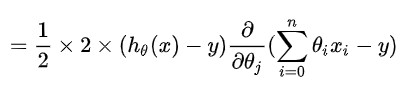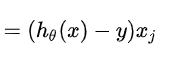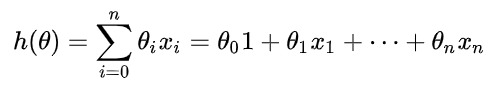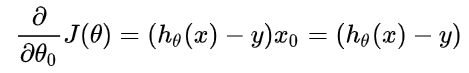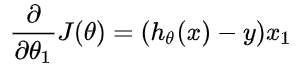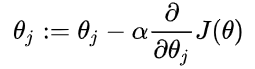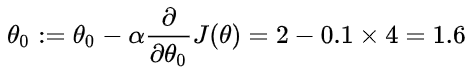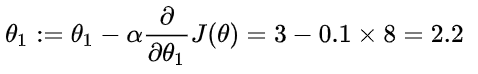前言
从这一篇文章开始，就正式进入「美团」算法工程师带你入门机器学习系列的正文了，之前的几篇算是导读和预热，想必大家看的并不过瘾。从这里开始，我们将会以线性回归为起点，贯通回归方法在机器学习算法中所扮演的角色、具有的功能和使用的方法。
说起回归，它是我们在高中时就接触过的内容。具体的，回归（Regression）是指研究一组随机变量(Y1 ，Y2 ，…，Yi)和另一组随机变量(X1，X2，…，Xk)之间关系的统计分析方法，又称多重回归分析。通常Y1，Y2，…，Yi是因变量，X1、X2，…，Xk是自变量。因变量，就是指被影响、决定的变量，本身不参与运算，而自变量则是指自身发生变化、改变并参与运算，最终影响因变量的变量。这些内容都是高中学习过的基础，这里仅仅做个回顾，不深入复习。
现在，让我们先抛开机器学习、算法、模型这类名词，从最简单的线性回归来看看，到底什么是回归（的诱惑）
线性回归是什么？
我们前面提到过，回归是计算因变量和自变量之间统计关系的一种方法。而线性回归可以理解为学习变量之间线性关系的方法。作为一切回归的基础，它已经存在了时间长了，是无数教科书的主题。
虽然看起来，线性回归与一些更现代的统计学习方法，比如支持向量机相比，有些过于简单。但在我们后续章节介绍的方法中，线性回归仍是一种非常有用的统计学习方法，它可以被用来简单的测试数据和分析数据。 基于这个出发点，许多有趣的机器学习方法可以被看作是概线性回归的扩展。在谈及具体的回归方法之前，让我们先来看看线性回归为什么叫回归。
在19世纪的英国，有一位著名的生物学家高尔顿，在研究父母和孩子身高的遗传关系时，发现了一个直线方程，通过这个方程，他几乎准确地拟合了被调查父母的平均身高 x 和 子女平均身高 y 之前的关系：
这在当时可是一件不得了的事情，那这个方程是什么意思呢？它代表父母身高每增加1个单位, 其成年子女的平均身高只增加0.516个单位，反映了一种“衰退”效应（“回归”到正常人平均身高）。虽然之后的x与 y变量之间并不总是具有“衰退”（回归）关系，但是为了纪念高尔顿这位伟大的统计学家，“线性回归”这一名称就保留了下来。
一元线性回归
回归最简单的情形是一元线性回归，也即由彼此间存在线性关系的一个自变量和一个因变量组成，方程写作Y=a+bX+ε（X是自变量，Y是因变量，ε是随机误差）我们先来看一个例子：
假设有如下数据点，横轴代表一个产品的广告费X，纵轴代表产品的销售额Y。回归可以看做是用Y=a+bX+ε这条直线去拟合这些数据点，也就是尽量使这些数据点与直线的距离之和（也叫作平方误差和）最小。
通过最小二乘法或梯度下降（后面会讲这两个方法），我们得到如下方程：
那么，当一个新的广告计划出现，我们通过已知的X（广告投入）代入方程，就可以尽可能准确的算出预期的产品销售额了~当然，反过来，使用一个预期的产品销售额，也可以反推出我们需要投入的广告费用。
多元线性回归
当自变量大于1的时候，比如X=(x1, x2)，我们称它为多元线性回归，写作
其中，y(x)也就是我们说的因变量，x为自变量，但是0次项和1次项的系数(a, b)被一个向量w所代替。这里的w是一个简单的矩阵线性乘法问题，对应了以下的向量
如果对于线性代数问题还有不理解的小伙伴，可以自行查阅《线性代数同济版》
来看一个例子：给定⼀个有关房屋的数据集，其中每栋房屋的相关数据包括⾯积（平⽅⽶）、房龄（年）和价格（元）。假设我们想使⽤任意⼀栋房屋的⾯积（设x1）和房龄（设x2）来估算它的真实价格（设y）。那么x1 和x2 即每栋房屋的特征（feature），y 为标签（label）或真实值（ground truth）。在线性回归模型中，房屋估计价格（设
）的表达式为
其中w1，w2 是权重（weight），通常用向量
来表示，b 是偏差（bias），也就是前面一元回归里我们用到的b。这⾥的权重和偏差都叫做线性回归模型的参数（parameter）
线性回归的假设
线性回归作为被严谨证明过的数学方法，有7个必备的假设前提。理论上，必须满足这7个严格的假设，我们才能确保线性回归学习到的公式/方程是统计意义成立的。但在实际使用时，我们只需要满足前3个最重要的假设即可（其他的一般都默认成立）。以后在学习其他算法前，我们也需要了解类似的假设。
关于线性回归，最主要的3条假设如下
- 随机误差的均值为0
- 随机误差的方差为σ^2
- σ^2与X的值无关
这里规定的σ^2并不是一个具体数值，只需要大于0即可。主要是为了说明随机误差的方差是存在的，方差（二阶中心矩）不存在，比如无限大，则这个模型就是病态的，这里涉及到高等代数，感兴趣的同学可以自行深入。
若进一步假定随机误差遵从正态分布，就叫做正态线性模型。若有k个自变量和1个因变量，则因变量的值分为两部分：一部分由自变量影响，即表示为它的函数，函数形式已知且含有未知参数；另一部分由其他的未考虑因素和随机性影响，即随机误差。
一般来说，随机误差在参数学习中起到的作用有限，但我们在真正使用模型时还是需要先看看数据是否满足线性回归的前提，否则容易对模型参数产生拟合问题。
线性回归的本质
一般来说，回归分析是通过规定因变量和自变量来确定变量之间的因果关系，建立回归模型，并根据实测数据来求解模型的各个参数，然后评价回归模型是否能够很好的拟合实测数据，如果能够很好的拟合，则可以根据自变量作进一步预测，比如我们提到的广告费用与产品销售额的关系。
当函数为参数未知的线性函数时，称为线性回归分析模型；当函数为参数未知的非线性函数时，称为非线性回归分析模型。当自变量个数大于1时称为多元回归，当因变量个数大于1时称为多元回归。
当X和Y只有一个维度（一元回归），且因变量和自变量的关系是线性关系，线性图表示就是一条直线，而多维度（多元回归）学习到的参数方程，体现到空间中就是一个超平面。
要注意的是，我们平时可能会把拟合与回归弄混淆，但其实二者有本质区别。你可以把现实世界的数据看做“表象”，把你拟合出来的那个模型看做“本质”。由表象到本质的过程就是“回归”。而拟合是一种得到函数的手段，常和数值领域的“插值”放在一起，也就是得到回归函数的手段。
当回归函数未知时，我们可以通过拟合这种手段算出回归函数，求这个回归函数的问题叫做回归问题。一个是问题的类别，一个是解决方法的类别，回归和拟合的差别就在这里。
数学理论的世界是精确的，譬如在广告-销量方程中，你代入x=0就能得到唯一的 y=7.1884，但这个y并不是我们真实观测到的，而是估计值。现实世界中的数据就像散点图，我们只能尽可能地在杂乱中寻找规律，很难100%的完美拟合一条直线出来。用数学的模型去拟合现实的数据，这就是统计。统计不像数学那么精确，统计的世界不是非黑即白的，它有“灰色地带”，但是统计会将理论与实际间的差别表示出来，也就是“误差”。
我们在前面学习到的公式，就是线性回归作为一种学习算法的本质，即模型
通过求解参数w，我们知道了自变量和因变量之间的线性关系，即我们拟合的直线
这个直线就是我们学习到的模型，尽可能地学习到一个完美的W，这就是线性回归的本质和作用，也是一切机器学习学习算法的本质——函数（参数）学习。
线性回归的参数学习
现在我们来看一看如何学习到这个完美的W。线性回归的目标可以理解为减少残差平方和，回到总体均值。在探究线性回归的学习方法之前，我们先定义如下表示，方便后续解释：
表示输入变量（自变量），第一部分例子中的X。
表示输出变量（因变量），第一部分例子中的Y。
一对
表示一组训练样本。
m个训练样本
称为训练集。
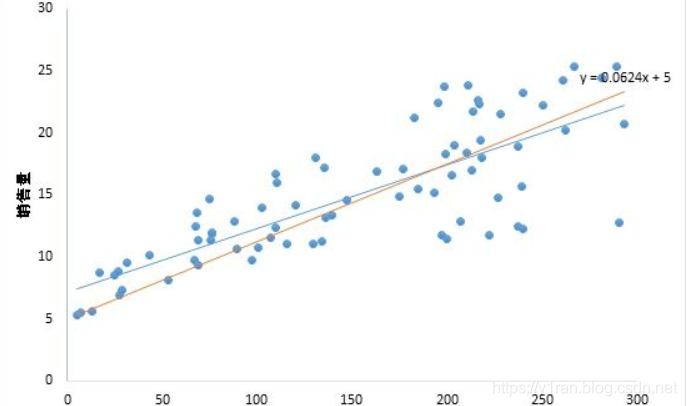
回到上面一元回归的例子来，既然是用直线拟合散点，为什么最终得到的直线是y = 0.0512x + 7.1884，而不是下图中的橙色的y = 0.0624x + 5呢？毕竟这两条线看起来都可以拟合这些数据。
我们很容发现，数据不是真的落在一条直线上，而是分布在直线周围，所以我们要找到一个评判标准，用于评价哪条直线才是最“合适”的。这就是我们以后时常会见到的东西——损失函数
在这里，我们使用的损失函数叫做残差，也就是真实值和预测值间的差值（也可以理解为距离），用公式表示是：
对于某个广告投入
，我们有对应的实际销售量
和预测出来的销售量（通过将
代入直线公式计算得到），计算 
的值，再将其平方（为了消除负号），将所有的 
相加，就能量化出拟合的直线和实际之间的误差。
这里使用的均方误差有非常好的几何意义，它对应了常用的欧几里得距离或简称"欧氏距离" (Euclidean distance)，也就是图里的数据点和直线之间的距离。基于均方误差最小化来进行模型求解的方法，称为“最小二乘法” (least square method)。在线性回归中，最小二乘法就是试图找到一条直线，使所有样本到直线上的欧氏距离之和最小。
最小二乘法
求解方程参数，使
最小化的过程，称为线性回归模型的最小二乘"参数估计" (parameter estimation)。我们可将E(w,b)分别对W 和b求导，得到
我们令上面两个式子的导数为零可得到W和b最优解的闭式(closed-form) 解（也就是可以直接通过公式代入算出来的解）
其中
，为X的均值
当X和Y为多元回归时，我们也有多元情况下的最小二乘法，写作
同样地，另这个偏导数为0，我们可以得到
这个东西也叫作正规方程，因为它很正规 (。≖ˇェˇ≖。)。具体的推导和运算涉及到矩阵的逆/伪逆，比单变量情形要复杂，这里不深入展开，感兴趣的同学可以自行翻阅《矩阵论》。这里我们只需要知道两点：
1. 现实任务中XTX 往往不是满秩矩阵.例如在许多任务中我们会遇到大量的变量，其数目甚至超过样例数，导致X 的列数多于行数，XTX 显然不满秩。此时可得到出无限个解， 它们都能使均方误差最小化
2. 我们的输入数据X（自变量），可以写作矩阵形式，矩阵的横轴代表每个数据的维度（比如房屋的价格，位置，年龄），纵轴代表每个房屋
学过线性代数的同学应该知道，当行、列很多时， 这个矩阵的任何运算都需要很大的计算量。尤其是输入变量的维度较大时（横轴的n比较大），该算法的计算复杂度成指数级增加。
因此，正规方程的解法在真实场景中很少见，我们有另一种叫做梯度下降的方法，通过损失一定精度，来近似逼近这个最优解。对于梯度方法，这里只做一个简单介绍，之后会有专门的一期文章来聊聊机器学习中的优化方法。
梯度下降
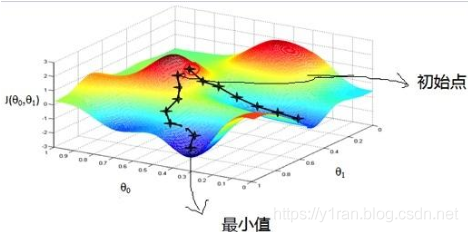
这里引用优化教材中的一张图，这里我们把参数W写作
，两者其实是一种东西。现在我们来思考：既然代价函数是关于的函数，有没有办法把求解过程加速或者拆解呢？
答案是有。
上图中的蓝色区域可以理解为误差函数最小的点，也就是我们要找的参数值，因此，找到该点对应的，即完成了任务。如何找到最低点位置对应的参数呢？答案是对代价函数（也就是我们的误差）求偏导数
我们用大学学过的微积分方法做一个拆解，可以得到：
这就是关于变量的偏导数。要注意的是，这里的h其实就是我们的y
假设我们的函数只有两个维度（二元回归），给定
就是我们要求的参数，误差函数对第一个元求偏导的结果：
误差函数对第二个元求偏导的结果：
求得的结果怎么使用？我们对 求偏导数的意义是得到这一点上的切线的斜率，它将给我们一个向最小值移动的方向。因此，减去偏导数，就等于向最小值的方向移动了一步。这一步的大小由一个参数决定，也称作学习率。用公式表达如下：
这就是机器学习中大名鼎鼎的的梯度下降。这个公式为什么这么写，有什么意义，之后在优化方法的文章中会写。对底层原理感兴趣的话，大家可以以前去看看MIT的微积分公开课（可汗学院、网易都有），以及Boyd所写的《凸优化》，到时候看博客就会非常通透。
这里举一个我在知乎上看到的例子，非常具体的解释了线性回归求解的过程
- 初始化一个模型，例如 h = 2 + 3x，也就是说，我们的初始参数是
- 给定一个样本对，例如（2，4），代入模型中求得预测值，即 h = 2 + 3*2 = 8
- 代入代价函数公式中，求代价值，即 J = 1/2 * (8-4) ^ 2 = 8
- 代入偏导数公式中求两个变量的偏导数，即
假设我们的学习率是0.1，那么代入梯度下降公式得到
我们得到了新的参数，即
比较新的模型得到的代价值2，比老模型得到的代价值8减少了6，代价越小说明我们的模型与训练集匹配的越好，所以通过不断的梯度下降，我们可以得到最适合训练数据的模型h，也就是前面提到的那条直线方程。
线性回归的局限
线性回归简单、直观、迅速，但也有不少局限，这也是之后更多高级算法的出现原因，它们一定程度上解决了线性回归无法解决的问题。线性回归的局限可以归纳以下几点：
- 需要严格的假设。
- 只能用于变量间存在简单线性关系的数据。
- 当数据量、数据维度大时，计算量会指数级增加。
- 需处理异常值，对异常值很敏感，对输入数据差异也很敏感。
- 线性回归存在共线性，自相关，异方差等问题。
结语
到这里，线性回归的文章就告一段落了。在这一篇文章中，我们通过线性回归，简单了解了机器学习的方式、概念和方法，但是对于更加具体的定义，比如模型、损失函数和监督学习还没讲到，这将是我之后文章的主题。下一期文章，我们将基于线性回归，来深入探讨回归的更多使用方法。
线性回归的Python代码和案例实战在这一篇：「06」回归的诱惑：一文读懂线性回归（Python实战篇） ，代码不多，建议大家可以自己敲一敲。
PS. 如果大家阅读其中的数学部分有些吃力的话，可以到我的这篇文章中找对应的知识点复习：「04」机器学习、深度学习需要哪些数学知识？
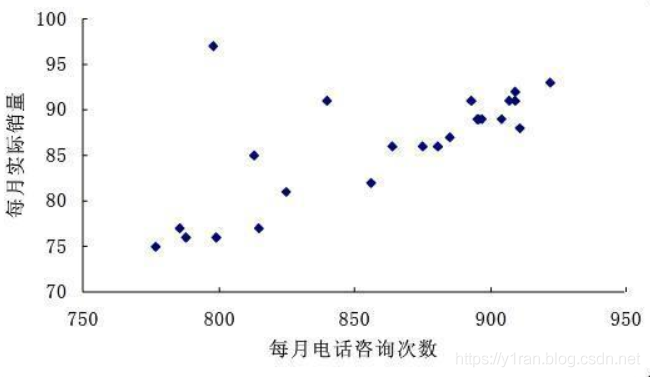
课后习题
给定每月电话咨询次数（X）和每月实际销量，线性回归是否可以把图中的数据点分为不同的两个部分？如果可以，应该怎么分？如果不可以，又是为什么？
