QAQ现在很不想写题解博客那就来写个算法吧QAQ...
带花树
题目
来看个题...
UOJ79.
某机房里有(n)个OIer,其中有(n)个男生,(0)个女生。现在他们要两两配对。
有(m)个关系,每个关系是一个无序对((a_i,b_i)),表示这两个人之间愿意配对。
求:最多能配成多少对,并找出一组方案。
说人话:一般图最大匹配。
算法
既然是匹配,我们能不能直接模仿匈牙利算法呢?答案是不可以(废话,可以的话还要什么带花树啊)。
原因是:我们在二分图中,如果dfs找增广路时经过某个点找不到,那么我们可以证明这一轮中这个点的确是无用的(也即,这一轮里所有的增广路都不经过这个点),于是我们就能保证每个点至多走一遍,时间复杂度得到保证。
但是如果是一般图,这个性质不一般成立。比如下图:
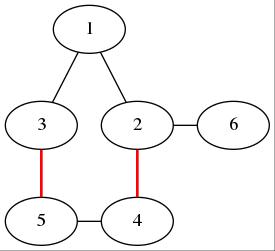
图中红线是已匹配的边。那么,如果我从(1)开始dfs时先经过(2),那么接下来就只能到(4)(因为只能走匹配边),然后是(5,3),同时我们会给这四个节点都打一个“找不到增广路”的标记。
但是实际上存在(1 ightarrow3 ightarrow5 ightarrow4 ightarrow2 ightarrow6)这条增广路。仔细观察我们就能发现:这种现象之所以存在,是由于奇环(1-3-5-4-2-1)的存在(如果没有奇环,就变成了二分图匹配,这时候匈牙利算法就是对的)。
那么,对于奇环,有什么后果呢?显然,如果我们dfs出了一个奇环,那么无论环上那个点dfs出了增广路都是可行的。(例如,上图中,如果从(5)处dfs出一条增广路,使得(5)匹配到别的点且(3)成为未盖点,那么可以走(1-3)。同样,如果(5)被孤立,我们可以走(1-2-4-5)来把(5)匹配上)
于是,我们可以把一个奇环当做一个点(这个奇环被称为“花”,这就是带花树名字的来历),然后继续找增广路。
形式化的,如果我们在图(G=(V,E))中找到了一个奇环(v_1-v_2-dots-v_k-v_1)(称为“花”),其中(v_1)是环上的深度最小的结点,不难证明,(v_1)的配偶不在此话中(因为在找到这个花之前所有边组成一个二分图,那么由于(v_1)向下dfs/bfs出了一个花,它一定是X结点,只有X结点会向外扩展),且((v_2,v_3),(v_4,v_5)dots(v_{k-1},v_{k}))都是匹配边。那么我们构建一个图
其中(f(v_i)=v_1, f(a)=a(a eq v_j), i, j=1,2,dots,k)
并且原本(G)中的所有匹配除掉((v_2,v_3),(v_4,v_5)dots(v_{k-1},v_{k}))构成(G')的一个匹配。
那么,(G)中存在增广路(Leftrightarrow)(G')中存在增广路。
证明:
(Rightarrow):对于(G)中的任意一条增广路,若其不经过这朵花,那么在(G')中也存在这条增广路;否则,令这条从(s)开始的增广路上的最后一个在花上的点为(v_j),那么这条增广路形如 (sleadsto v_j leadsto t),我们在(G')上构造如下增广路:先从(s leadsto v_1 leadsto t),其中第一段路程沿着bfs/dfs树走,第二段路程沿着原图中的增广路走,唯一不同的是(v_j)变成了(v_1)(这是合法的,因为所有从(v_j)出发的边都被连到了(v_1)上,而且我们根据所有(v)都是已盖点可以知道(v_j)出发的边是非匹配边)。
(Leftarrow):对于(G')中的一条增广路,若它不经过(v_1),则(G)中也存在;否则,设这条增广路为(sleadsto v_1 ightarrow x leadsto t)((x)可能等于(t)),根据(E')的定义存在((v_i, x)in E),从而我们构造(G)中的增广路:(sleadsto v_1leadsto v_i ightarrow x leadsto t),其中第一段和第三段不变(因为增广路上(v_1)至多出现1次,所以这两段在(G)中存在),第二段是在花里走(或者精确一点,若(i)是奇数,走(v_1 ightarrow v_2 dots v_i),否则走(v_1 ightarrow v_k dots v_i)。证毕。
bfs时,我们可以(O(n))求出LCA并(O(kn))缩花,从而单次bfs至多(O(n^2)),总复杂度至多(O(n^3))。
实现上,我们不实际缩点,而是对于每个点维护一个(fa),表示它所处的最大的花的LCA(就是(v_1))。由于花里可能还有花,这个(fa)要用并查集维护。在证明中构造增广路是通过判断(i)奇偶性,但实际上我们可以直接维护每个点要往哪边走,也即维护一个(link_i)表示如果(i)失配要和谁匹配(例如,(link_{v_2}=v_1,link_{v_3}=v_4))。找LCA的时候直接暴力(O(n)),但要注意只找每个并查集的根节点(因为非根节点都缩到花里了);缩花时要注意如果两个点已经在一朵花里就不要再缩了。
代码
#include <algorithm>
#include <cstdio>
const int N = 550;
const int M = 250050;
int pre[N], nxt[M], to[M], cnt, n;
int vis[N], fa[N], link[N], mate[N];
int que[N], head, tail;
int ss[N], time;
inline void addEdge(int x, int y) {
nxt[cnt] = pre[x];
to[pre[x] = cnt++] = y;
}
int Find(int x) { return fa[x] == x ? x : fa[x] = Find(fa[x]); }
int LCA(int x, int y) {
++time;
while (ss[x] != time) {
if (x) {
ss[x] = time;
x = Find(link[mate[x]]);
}
std::swap(x, y);
}
return x;
}
void flower(int x, int y, int p) {
while (Find(x) != p) {
link[x] = y;
fa[y = mate[x]] = fa[x] = p;
if (vis[y] == 1)
vis[que[tail++] = y] = 2;
x = link[y];
}
}
bool match(int x) {
head = tail = 0;
for (int i = 1; i <= n; ++i)
vis[fa[i] = i] = 0;
vis[que[tail++] = x] = 2;
while (head != tail) {
x = que[head++];
for (int i = pre[x]; ~i; i = nxt[i]) {
int u = to[i];
if (!vis[u]) {
vis[u] = 1;
link[u] = x;
if (mate[u])
vis[que[tail++] = mate[u]] = 2;
else {
while (u) {
x = mate[link[u]];
mate[mate[u] = link[u]] = u;
u = x;
}
return true;
}
} else if (vis[u] == 2 && Find(u) != Find(x)) {
int p = LCA(x, u);
flower(x, u, p);
flower(u, x, p);
}
}
}
return false;
}
int main() {
int m, x, y, ans = 0;
scanf("%d%d", &n ,&m);
std::fill(pre + 1, pre + n + 1, -1);
while (m--) {
scanf("%d%d", &x, &y);
addEdge(x, y);
addEdge(y, x);
if (!mate[x] && !mate[y])
mate[mate[x] = y] = x, ++ans;
}
for (int i = 1; i <= n; ++i)
if (!mate[i] && match(i))
++ans;
printf("%d
", ans);
for (int i = 1; i <= n; ++i)
printf("%d ", mate[i]);
return 0;
}