Pick定理、欧拉公式和圆的反演
Tags:高级算法
Pick定理
内容
定点都是整点的多边形,内部整点数为(innod),边界整点数(ednod),(S=innod+frac{ednod}{2}-1)
证明
把每个整点近似地看成一个圆,那么多边形内部的整点所代表的圆全部被算入
多边形边界上的圆被算了一半
顶点上被算了(sum 半圆-外角),外角和360度,于是(-1)
应用
POJ2954 求格点三角形内部点数
欧拉公式
内容
[V-E+F=2
]
(V:vertex) 顶点
(E:edge) 边
(F:Flat) 面
适用于所有多变形(无论维度)
例如一个长方形:(4)个点(4)条边,两个面:里面和外面
应用
(n)个点做三维凸包,求增量构造法复杂度。
假设(n)个点都在凸包上,那么(V=n),每个面有三条边,每条边被算了两次,即(2E=3F)
通过上面的公式可以得到(F=2n-4,E=3n-6)。
增量构造法的复杂度是面数×点数,所以是(cal O(n^2))级别
圆的反演变换
内容
反演中心为(O),反演半径为(R),若经过(O)的直线经过(P,P'),且(OP*OP'=R^2),则称(P)、(P')关于(O)互为反演
性质
- 1.一根过(O)的直线的反形是本身
- 2.一根不过(O)的直线的反形是一个过(O)的圆
- 3.一个过(O)的圆的反形是一根不过(O)的直线
- 4.一个不过(O)的圆的反形是一个和该圆关于(O)位似的圆
下面这张图可以粗略解释一下有这么个东西:两种不同颜色的三角形相似,可以证出(CD)关于(E)的反形为圆
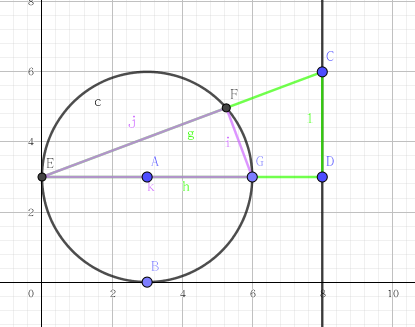
- 5.反演不改变相切关系
应用
1、求平面内与原点四点共圆的三元组个数
Problem Provider:自为风月马前卒
对所有点反演后求三点共线的三元组即可
2、求经过P点并与两给定相离圆外切的圆
参考博客:ACdreamer反演教程、水郁图文、cdsszjj题解、教你尺规画图
Problem Provider:HDU4773 Problem of Apollonius
先将两相离圆关于P反演,然后做反形的公切线,反演回来成为公切圆