并不对劲的辛普森积分

并不会计算几何的并不对劲的人想必是非常之菜的。

很对劲的太刀流在这里->

辛普森积分本身是把一段函数f(x)当成二次函数算，用(f(l)+4*f((l+r)/2)+f(r))*(r-l)/6算出这段曲线在l到r之间与x轴所夹面积。

但是这听上去非常不精确，所以有人发明了自适应的辛普森积分。   

每一次分别算出这段左一半、右一半和整个的辛普森积分，如果左+右与整个之差大于eps就继续递归处理左、右半部分。

至于为什么不把一段函数当成一次函数算，是因为会被f(mid)恰好在直线上这种数据卡：

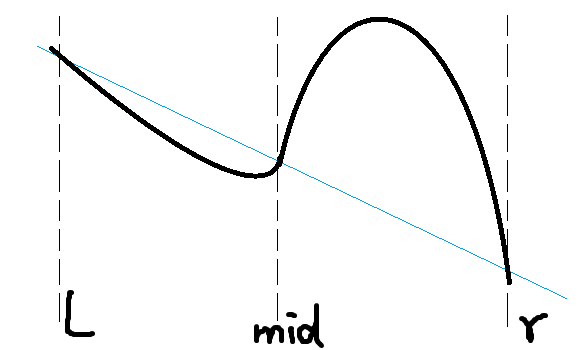
而二次函数只能用这种手形数据卡：

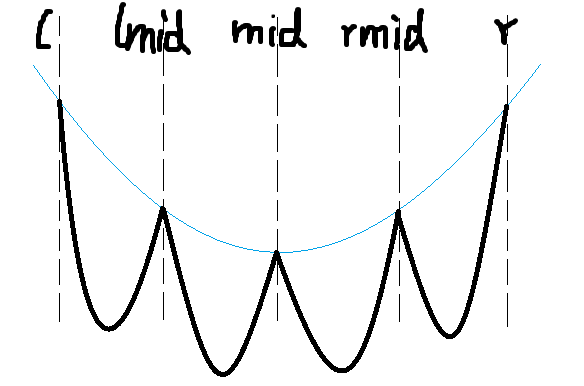
那为什么不用三次函数呢？想必是因为三次函数复杂的让人手不健康而且手形数据不是那么好构造吧。

————————例题分界线————————
bzoj2178: 圆的面积并
Time Limit: 20 Sec Memory Limit: 259 MB
Submit: 2415 Solved: 617
[Submit][Status][Discuss]
Description
给出N个圆，求其面积并
Input
先给一个数字N ,N< = 1000 接下来是N行是圆的圆心，半径，其绝对值均为小于1000的整数
Output
面积并，保留三位小数
————————题解分界线—————————
可以把直线x=x₁ 在圆中的部分的长度看成是关于x₁的函数。对这个函数求自适应的辛普森积分，但是复杂度非常之玄学。

经某些人的实验，发现eps设为1e-14会TLE，设为1e-12会WA，所以好像没什么可选的…

注意要删去所有被包含的圆、加一堆常数优化才能过。

#include<iostream>
#include<iomanip>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#define fir first
#define sec second
#define eps (1e-13)
#define maxn 1010
#define four 4.0
#define six 6.0
#define two 2.0
#define re register 
using namespace std;
typedef pair<double,double>Pdd; 
typedef struct point{double x,y;}P;
typedef struct circle
{
    P o;
    double r;
    bool operator <(const circle &z)const{ return o.x<z.o.x;}
    Pdd getd(double x)  
    {  
        if(r<=fabs(o.x-x))   return Pdd(0,0);//相离 
        double dis=sqrt(r*r-(o.x-x)*(o.x-x));  
        return Pdd(o.y-dis,o.y+dis); //下、上交点 
    }  
}C;
int n,no[maxn],cntt;
double minl=10101010.0,maxr=-10101010.0;
C cir[maxn],circ[maxn];
Pdd pd[maxn];
double D(P _1,P _2){return sqrt((_1.x-_2.x)*(_1.x-_2.x)+(_1.y-_2.y)*(_1.y-_2.y));}

double getf(double x)
{//此线在多个圆中的部分的并 
    double ans=0,last=-10101010;  
    int cnt=0;  
    for(re int i=1;i<=cntt;i++)  
    {  
        pd[++cnt]=circ[i].getd(x);  
        cnt=(pd[cnt]==Pdd(0,0))?cnt-1:cnt;  
    }  
    sort(pd+1,pd+cnt+1);  
    for(re int i=1;i<=cnt;i++)  
    {  
        if(pd[i].fir>last)  
            ans+=pd[i].sec-pd[i].fir,last=pd[i].sec;   
        else if(pd[i].sec>last)  
            ans+=pd[i].sec-last,last=pd[i].sec;  
    }  
    //printf("***%.8lf %.8lf***",x,ans);
    return ans;  
} 
inline double getsim(double l,double r,double fl,double fm,double fr){return ((r-l)/six)*(fl+four*fm+fr);}
double simpson(double l,double m,double r,double fl,double fm,double fr)
{//是对f(x)表示直线x在圆内的部分的总长度这个函数求积分 
    double lm=(l+m)/two,rm=(m+r)/two,flm=getf(lm),frm=getf(rm);
    double lans=getsim(l,m,fl,flm,fm),rans=getsim(m,r,fm,frm,fr),totans=getsim(l,r,fl,fm,fr);
    //printf("%.8lf %.8lf %.8lf %.8lf
",l,r,lans+rans,totans);system("pause");
    if(fabs(lans+rans-totans)<=eps)return totans;
    else return simpson(l,lm,m,fl,flm,fm)+simpson(m,rm,r,fm,frm,fr);
}
int main()
{
    memset(no,0,sizeof(no));
    scanf("%d",&n);
    for(re int i=1;i<=n;i++)
    {
        scanf("%lf%lf%lf",&cir[i].o.x,&cir[i].o.y,&cir[i].r);
        if(minl>cir[i].o.x-cir[i].r)minl=cir[i].o.x-cir[i].r;
        if(maxr<cir[i].o.x+cir[i].r)maxr=cir[i].o.x+cir[i].r;
    }
    sort(cir+1,cir+n+1);
    for(re int i=1;i<=n;i++)
    {
        if(no[i])continue;    
        for(int j=i+1;j<=n;j++)
        {
            if(no[j])continue;
            if(D(cir[i].o,cir[j].o)+cir[j].r<=cir[i].r)  
                no[j]=1;  
        }
    }//去除被包含的圆 
    for(re int i=1;i<=n;i++)
        if(!no[i])circ[++cntt]=cir[i];
    double ans=simpson(minl,(minl+maxr)/two,maxr,0,getf((minl+maxr)/two),0);
    printf("%.3lf",ans);
    return 0;
}

宣传一波电教，欢迎加入。