5. 快速排序

一、基本思想

通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以使整个序列有序。

在分割的过程中，枢纽元的选择至关重要。原因如下：

　　（1）两部分数据是以枢纽元为分界点，小于等于枢纽元的数全部放在枢纽元的左边，而大于等于枢纽元的数全部放在枢纽元的右边；

　　（2）一般选用左端、右端和中心位置上的三个元素的中值作为枢纽元，即三数取中法，它可以很大程度上避免分组“一边倒”的情况。

二、三数取中

在快排的过程中，每一趟排序我们都要取一个元素作为枢纽值，以这个数字来将序列划分为两部分。

在此我们采用三数取中法，也就是取左端、中间、右端三个数，然后进行排序，将中间数作为枢纽值。

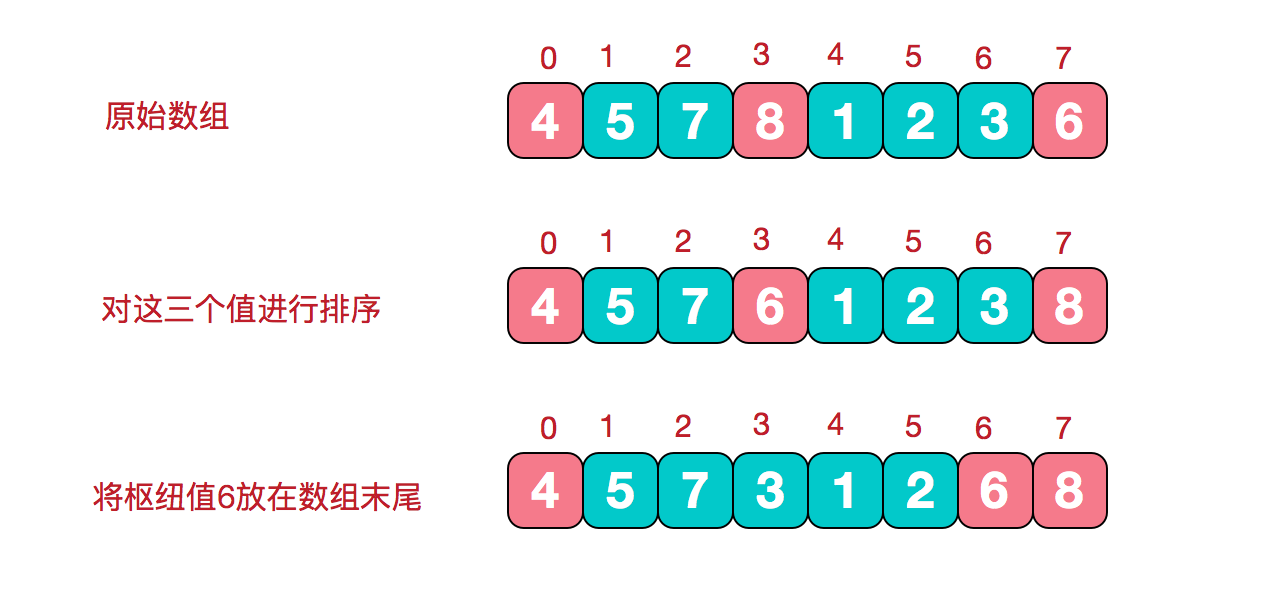
三、根据枢纽值进行分割

四、代码

/* 快速排序 */ 
void QuickSort(int a[], int left, int right)
{
	if(left >= right)
		return;
	
	// 采用三数取中法，获取枢纽元，并将其放在当前待处理序列末尾 
	DealPivot(a, left, right);
	int pivot = a[right-1];			// pivot为枢纽元，而其下标为right-1 

	int i = left, j = right - 1;	// 设置两个游标，用以标记待排序区间
	// 当 i = j 时，已经查找完整个区间了 
	while(i != j) {
		while(i < j && a[i] <= pivot) 	// 因为枢纽元在右边，所以从左边开始 
			++i;
		while(i < j && a[j] >= pivot)
			--j;
		if(i < j)
			swap(a[i], a[j]);
	}
	// 此时 i = j 
	swap(a[i], a[right-1]);	
		
	sort(a, left, i-1);
	sort(a, i+1, right);
}

// 处理枢纽元 
void DealPivot(int a[], int left, int right)
{
	int mid = (left + right) / 2;
	if(a[left] > a[mid])
		swap(a[left], a[mid]);
	if(a[left] > a[right])	
		swap(a[left], a[right]);
	if(a[mid] > a[right])
		swap(a[mid], a[right]);
	swap(a[mid], a[right-1]);		// 将枢纽元放到倒数第二个元素去，所以要先从左边检索 
}