2. 希尔排序

一、介绍

希尔排序属于插入排序，它是对直接插入排序改进后的一个更高效的版本，也称为缩小增量排序。

该算法是冲破O(n²)的第一批算法之一，它的平均复杂度为O(n^1.3)，最坏时间复杂度为O(n²)。

二、基本思想

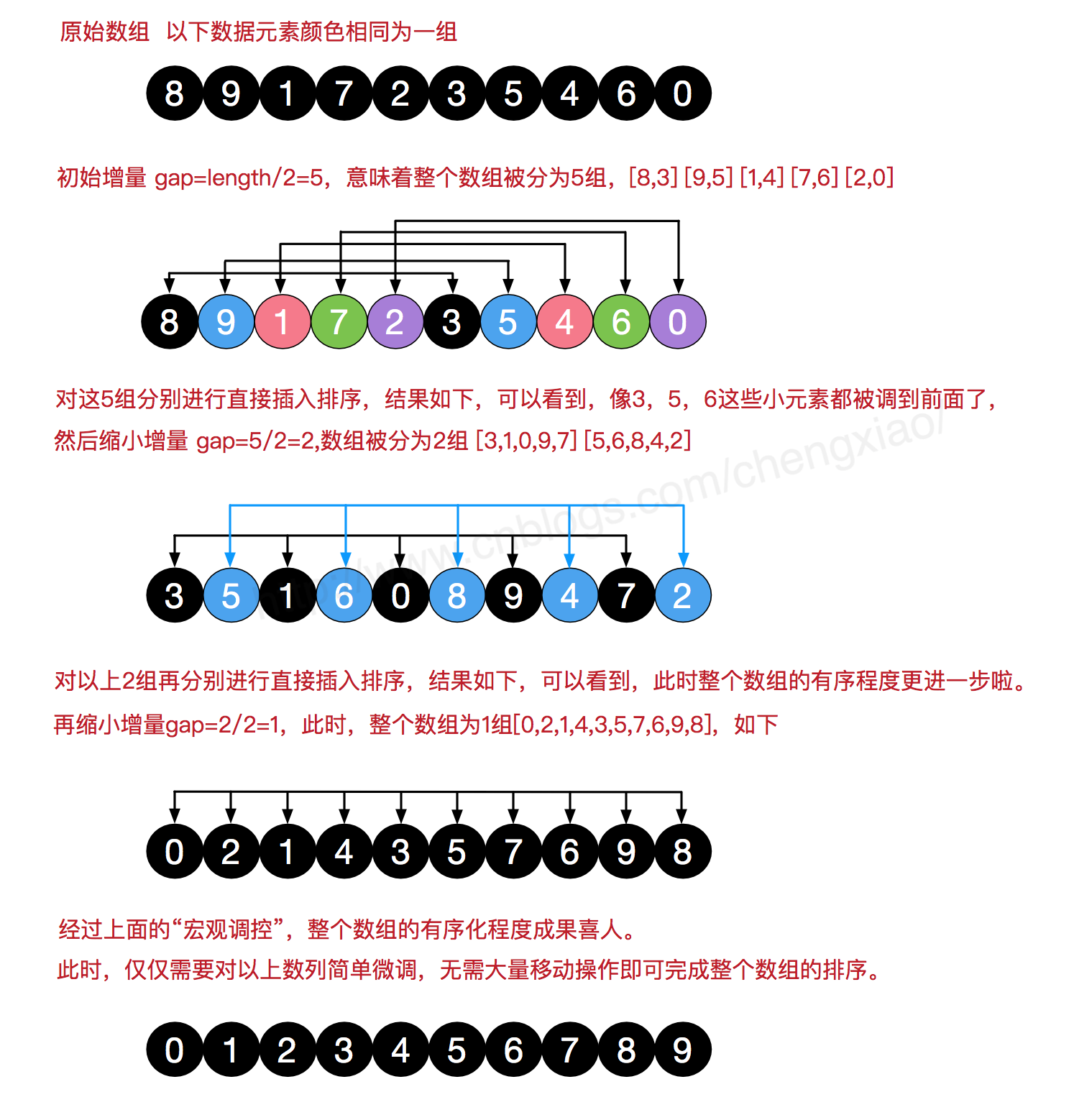
对于一个具有n个元素的数组，取一个增量(gap)将其分组（距离为gap的倍数的元素放在同一个组中，跳跃式分组），对各组内的元素进行直接插入排序。 这一趟排序完成之后，每一个组的元素都是有序的。然后减小gap的值，并重复执行上述的分组和排序。重复这样的操作，当gap=1时，所有元素恰被分为一组，算法终止。

当gap=1时，整个数组从宏观上看基本有序，小的基本在前，大的基本在后。这时的数组只需微调即可，不会涉及过多的数据移动。

【增量(gap)的选择】

增量的初始值为gap = n / 2，并以 gap = gap / 2 的方式缩小增量。

增量值的取值可以用一个序列来表示，即{n/2, (n/2)/2, ..., 1}。此序列也被称为增量序列。

三、代码

/* 希尔排序 */ 
void shellSort(int a[], int n)
{
	int gap = n / 2;
	
	for(; gap >= 1; gap = gap / 2) {
		// 共gap个组，对每一组都执行直接插入排序
		for(int i = 0; i < gap; ++i) {
			// 对一个组进行直接插入排序 
			for(int j = i + gap; j < n; j = j + gap) {
				// 后面的数更小，则需要将其插入到前面某个位置，并调整相应的元素 
				if(a[j] < a[j-gap]) {
					int temp = a[j];
					int k = j - gap;
					while(k >= 0 && a[k] > temp) {
						a[k+gap] = a[k];
						k = k - gap;
					}
					a[k+gap] = temp;	// 这个新元素被插入到合适的位置 
				}
			}	// 一个数组调整完毕 
		}	// 由该gap分成各个数组已分别排序完毕 
	}
}