1. 拓扑排序

一、定义

拓扑排序：对有向无环图的顶点的一种排序，它使得如果存在一条从v_i到v_j的路径，那么在排序中v_j出现在v_i的后面。

对一个有向无环图G进行拓扑排序，是将G中所有顶点排成一个线性序列，使得图中任意一对顶点u和v，若边<u,v>∈E(G)，则u在线性序列中出现在v之前。

示例：在学习课程图中，存在有向边<C语言, 数据结构>，则对该图进行拓扑排序后，在生成的线性序列中，C语言一定排在数据结构之前。

二、AOV网

引子：现有一个工程亟待完成，我们需要制作施工的流程图，它可以决定哪些子工程必须要先执行，哪些子工程要在某些工程执行后才可以执行。为了形象地反映出整个工程中各个子工程之间的先后关系，可用一个有向图来表示，图中的顶点代表活动（子工程），图中的有向边代表活动的先后关系。

定义：我们把这种顶点表示活动、边表示活动间先后关系的有向图称做顶点活动网，简称AOV网。

一个AOV网应该是一个有向无环图，即不应该带有回路，因为若带有回路，则回路上的所有活动都无法进行（对于数据流来说就是死循环）。

在AOV网中，若不存在回路，则所有活动可排列成一个线性序列，使得每个活动的所有前驱活动都排在该活动的前面，我们把此序列叫做拓扑序列，由AOV网构造拓扑序列的过程叫做拓扑排序。

注：拓扑序列可能不是唯一的；AOV网必须是无环的，因为只有有向无环图才能形成拓扑序列。

三、算法过程

1. 在有向图中选一个没有前驱的顶点并且输出
2. 从图中删除该顶点和所有以它为尾的弧（白话就是：删除所有和它有关的边）
3. 重复上述两步，直至所有顶点输出，或者当前图中不存在无前驱的顶点为止，后者代表我们的有向图是有环的，因此，也可以通过拓扑排序来判断一个图是否有环。

下图是一个AOV网，要求对其进行拓扑排序。

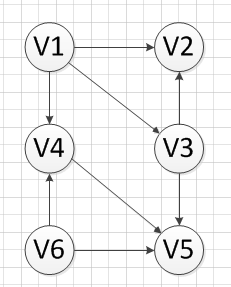
（1）我们发现V6和v1是没有前驱的，所以我们就随机选去一个输出，我们先输出V6，删除和V6有关的边，得到如下图结果：

（2）我们继续寻找没有前驱的顶点，发现V1没有前驱，所以输出V1，删除和V1有关的边，得到下图的结果： 

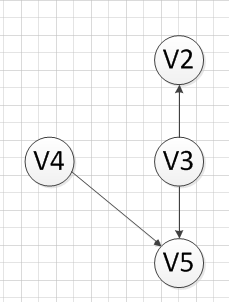
（3）我们又发现V4和V3都是没有前驱的，那么我们就随机选取一个顶点输出（具体看你实现的算法和图存储结构），我们输出V4，得到如下图结果：

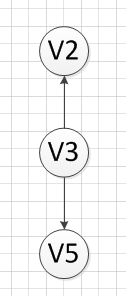
（4）我们输出没有前驱的顶点V3，得到如下结果：

（5）我们分别输出V5和V2，此时全部顶点输出完成

该图的一个拓扑序列为：V6 ---> V1 ---> V4 ---> V3 ---> V5 ---> V2