我本来想给这篇博客起名贪心法,但还是换成了贪心思想。我是想理解这种思想,而非只会“贪心法”这三个字。
贪心法是一种解决问题的策略。
下面我们就借助一些可用贪心法解决的经典问题来学习一下贪心思想。
经典问题一:背包相关问题
【最优装载问题】
给出n个物体,第 i 个物体重量为wi 。选择尽量多的物体,使得总重量不超过C 。
由于只关心物体的数量,所以装重的没有装轻的划算。只需把所有物体按重量从小到大排序,依次选择每个物体,直到装不下为止。
这是一种典型的贪心算法,它只顾眼前,但却能得到最优解。
【部分背包问题】
有n个物体,第 i 个物体的重量为wi,价值为vi。在总重量不超过C的情况下让总价值尽量高。每一个物体可以只取走一部分,价值和重量按比例计算。
本题不能简单地向上题那样先拿轻的(轻的可能价值也小),也不能先拿价值大的(可能它特别重),而应该综合考虑两个因素。一种直观的贪心策略是:优先拿“价值除以重量的值”最大的,直到重量和正好为C 。
【乘船问题】
有n个人,第 i 个人重量为wi。每艘船的最大载重量均为C,且最多只能乘两个人。用最少的船装载所有人。
考虑最轻的人 i,他应该和谁一起坐呢?如果每个人都无法和他一起坐船,则唯一的方案就是每人坐一艘船。否则,他应该选择能和他一起坐船的人中最重的一个 j 。
这样的方法是贪心的,因为它只是让“眼前”的浪费最少。幸运的是,这个贪心策略也是对的,可以用反证法说明。
假设这样做不是最好的,那么最好方案中 i 是什么样的呢?
- 情况1:i 不和任何一个人坐同一艘船,那么可以把 j 拉过来和他一起坐,总船数不会增加(而且可能会减少)。
- 情况2:i 和另外一人k同船。由贪心策略,j 是“可以和 i 一起坐船的人”中最重的,因为k比 j 轻。把 j 和 k 交换后 k 所在的船仍然不会超重(因为 k 比 j 轻),而 i 和 j 所在的船也不会超重(由贪心法过程),因此所得到的新解不会更差。
由此可见,贪心法不会丢失最优解。最后说一下程序实现。在刚才的分析中,比 j 更重的人只能每人坐一艘船。这样,只需用两个下标 i 和 j 分别表示当前考虑的最轻的人和最重的人,每次先将 j 往左移动,直到 i 和 j 可以共坐一艘船,然后将 i 加1,j 减1,并重复上述操作。不难看出,程序的时间复杂度仅为O(n),是最优算法(别忘了,读入数据也需要O(n)时间,因此无法比这个更好了)。
经典问题二:区间相关问题
【选择不想交区间】
数轴上有n个开区间(ai, bi)。选择尽量多个区间,使得这些区间两两没有公共点。
首先明确一个问题:假设有两个区间x,y,区间x完全包含y。那么,选x是不划算的,因为x和y最多只能选一个,选x还不如选y,这样不仅区间数目不会减少,而且给其他区间留出了更多的位置。接下来,按照bi从小到大的顺序给区间排序。贪心策略是:一定要选第一个区间。为什么?
现在区间已经排序成b1<=b2<=b3...了,考虑a1和a2的大小关系。
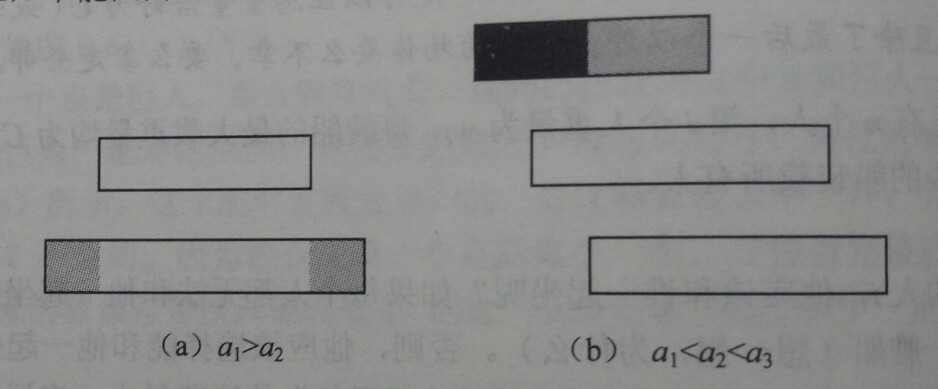
- 情况1:a1>a2,如下图所示,区间2包含区间1。前面已经讨论过,这种情况下一定不会选择区间2,而且不仅区间2如此,以后所有区间中只要有一个 i 满足a1>ai,i 都不要选。在今后的讨论中,将不考虑这些区间。
- 情况2:排除了情况1,一定有a1<=a2<=a3<=...,如下图所示。如果区间2和区间1完全不相交,那么没有影响(因此一定要选区间1),否则区间1和区间2最多只能选一个。如果不选区间2,黑色部分其实是没有任何影响的(它不会挡住任何一个区间),区间1的有效部分其实变成了灰色部分,它被区间2所包含!由刚才的结论,区间2是不能选的。依此类推,不能因为选任何区间而放弃区间1,因此选择区间1是明智的。选择了区间1以后,需要把所有和区间1相交的区间排除在外,需要记录上一个被选择的区间编号。这样,在排序后只需要扫描一次即可完成贪心过程,得到正确结果。
【区间选点问题】
数轴上有n个闭区间[ai, bi] 。取尽量少的点,使得每个区间内都至少有一个点(不同区间内含的点可以是同一个)。
如果区间 i 内已经有一个点被选到,则称此区间已经被满足。受上一题的启发,下面先讨论区间包含的情况。由于小区间被满足时大区间一定也被满足,所以在区间包含的情况下,大区间不需要考虑。
把所有区间按b从小到大排序(b相同时a从大到小排序),则如果出现区间包含的情况,小区间一定排在前面。第一个区间应该取哪一点呢?此处的贪心策略是:取最后一个点,如下图所示。
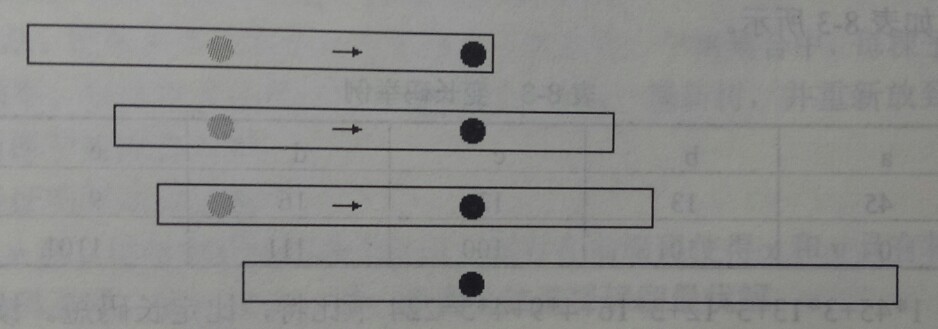
根据刚才的讨论,所有需要考虑的区间的a也是递增的,可以把它画成上图的形式。如果第一个区间不取最后一个,而是取中间的,如灰色点,那么把它移动到最后一个点后,被满足的区间增加了,而且原先被满足的区间现在一定被满足。不难看出,这样的贪心策略是正确的。
【区间覆盖问题】
数轴上有n个闭区间[ai, bi],选择尽量少的区间覆盖一条指定线段[s, t] 。
本题的突破口仍然是区间包含和排序扫描,不过先要进行一次预处理。每个区间在[s, t]外的部分都应该预先被切掉,因为它们的存在是毫无意义的。预处理后,在相互包含的情况下,小区间显然不应该考虑。
把各区间按照a从小到大排序。如果区间1的起点不是s,无解(因为其他区间的起点更大,不可能覆盖到s点),否则选择起点在s的最长区间。选择此区间[ai, bi]后,新的起点应该设置为bi,并且忽略所有区间在bi之前的部分,就像预处理一样。虽然贪心策略比上题复杂,但是仍然只需要一次扫描,如下图所示。s为当前有效起点(此前部分已被覆盖),则应该选择区间2。

经典问题三:Huffman编码
现在还不懂,参考紫书P234。