1.选择合适的损失函数
典型的损失函数有平方误差损失函数和交叉熵损失函数
交叉熵损失函数:
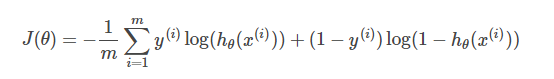
不同的损失函数的选择会对训练结果产生影响
2.mini-batch和epoch
所谓mini-batch是把我们原来的数据分成了不重叠的若干个小的数据块,然后在每一个epoch中分别运行每一个mini-batch,epoch的次数和mini-batch的大小我们自行设定
进行mini-batch和epoch划分的原因
之所以要进行mini-batch和epoch的改变,一个很重要的原因是这样就可以实现并行计算。但是这样的话,每一次的L就不是全局损失而是局部损失。mini-batch采用了并行计算会比之前传统算法的速度更快。并且mini-batch的效果会比传统的方法好
mini-batch和epoch的缺点
mini-batch是不稳定的。mini-batch不一定会收敛。
3.新的激励函数
深度学习并不是说神经网络的层数越多越好。因为神经网络的深度越深那么在误差回传的过程中,因为层数过多可能会有梯度消失的问题。所谓梯度消失问题指的是在训练的过程中,越靠近输出层的学习的越快越靠近输入层的学习的越慢。那么随着深度的增加,靠近输出层的隐含层权重已经收敛了,但是靠近输入层的隐含层却还没有什么变化,相当于还是像初始的时候一样权重是随机的。
为了梯度消失的问题,学者提出了使用ReLU函数作为激励函数。以下是ReLU函数
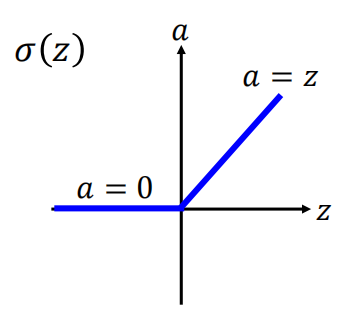
(1)为什么要选择ReLU函数作为激励函数
1.很容易计算
2.Relu函数和我们神经元的激励机制很像:神经元只有在接收一定量的刺激才能够产生反应
3.infinite sigmoid with different biases【这句话不知道咋解释】
4.解决梯度消失问题
(2)ReLU函数的变种
ReLU函数有很多种形式,上面的函数图像只是其中最原始的一种。还有Leaky ReLU和Parametric ReLU

Maxout激励函数
Maxout激励函数先将隐含层的神经元进行分组然后利用分段函数得到组中每一个elements的值,取最大的输出。这个分段函数分的段数是取决于一个group里面有多少个elements。其实ReLU就是一个group里面只有一个element的Maxout激励函数
自适应的学习率
学习率是一个很重要的参数,如果学习率选择的太大的话就会出现无法收敛的情况,如果学习率选择的太小的话收敛的太慢,训练过程太长。
我们选择学习率一般不是选择一个固定的值,而是让它随着训练次数的不断增加而减少。学习率针对不同的参数应该是不同的。并且对于所有的参数来说学习率应该越来越小。导数越大,学习率越小;导数越小,学习率越大。【这里导数是有正负性的】
Momentum
单纯的使用导数用于改变学习率,很容易陷入局部最小,或者极值点。为了避免这一点,我们使用了Momentum。虽然加上Momentum并不能完全的避免陷入局部最小,但是可以从一定的程度上减缓这个现象。
过拟合
所谓的过拟合,就是过度的学习训练集的特征,将训练集独有的特征当做了数据的全局特征,使得其无法适应测试集的分布。
防止过拟合的方法叫做正则化,正则化的方式有很多。
在神经网络中正则化的方法主要有四种:
1.早起停止(eary stopping):比如我们可以设置训练的最大轮数等
2.权重衰减:减少无用的边的权重
3.droupout:每次训练的时候都删除一些节点单元,这样会使网络结构变得简单,训练过程也变得更加简单。它的定义是如果你在训练的阶段对于某一层删除了p%节点,那么你在训练时该层的神经元的权重也要衰减p%。droupout可以看做是一个ensamble的过程。
4.网络结构:比如CNN