题意
给一颗树,删除一条边再加一条边,使它仍为一颗树且任意两点间的距离的最大值最小。
题目数据范围描述有问题,n为1或重建不能使任意两点距离最大值变小,可以输出任意答案。
分析
删除一条边后会使它变成两颗树,两棵树的直径的中点相连一定是使距离最小的
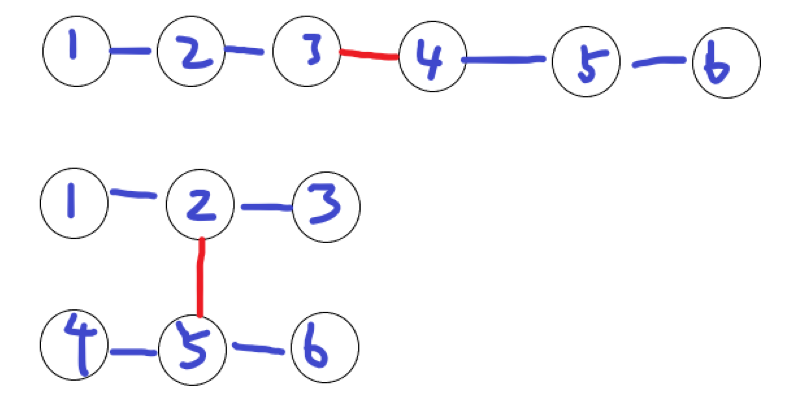
红色的边为删除重建的边
在树上dp维护每个子树的最大直径(h[x]),和去除这个子树后的树的最大直径(t[x]),u为x的父亲,删除u-x这条边并重建后的树的最大直径为
[max{frac{h[x]+1}{2}+frac{t[x]+1}{2}+1,h[x],t[x]}
]
设(g[u])为以(u)为根的子树中(u)能到达的最远距离
设(p[u])为去除以(u)为根的子树后(u)能到达的最远距离
自底向上
x为u的孩子,(mx1),(mx2)分别为(g[x])的最大值和次大值
- (g[u]=max(g[x]+1))
- (h[u]=max{h[x],g[u],mx1+mx2+2})
自顶向下
k为x的兄弟,(mx1),(mx2)分别为(g[k])的最大值和次大值
- (p[x]=max(p[u]+1,g[k]+2))
- (t[x]=max {p[u],h[k],p[u]+g[k]+1,mx1+mx2+2 })
然后bfs找重建的边
实现细节很多,我写的比较乱,建议自己根据dp式子模拟一下
Code
#include<bits/stdc++.h>
#define fi first
#define se second
#define bug cout<<"--------------"<<endl
using namespace std;
typedef long long ll;
const double PI=acos(-1.0);
const double eps=1e-6;
const int inf=1e9;
const ll llf=1e18;
const int mod=1e9+7;
const int maxn=3e5+10;
int n;
vector<int>f[maxn];
typedef pair<int,int> pii;
pii e[maxn];
int g[maxn],h[maxn],p[maxn],t[maxn];
int ans=inf;
pii ans1,ans2;
void dfs1(int u,int fa){
int mx1=-inf,mx2=-inf;
int len=f[u].size();
int po=len;
for(int i=0;i<len;i++){
int x=f[u][i];
if(x==fa){
continue;
}
dfs1(x,u);
g[u]=max(g[x]+1,g[u]);
if(g[x]>mx1){
mx2=mx1;
mx1=g[x];
}else if(g[x]>mx2){
mx2=g[x];
}
h[u]=max(h[u],h[x]);
}
h[u]=max(h[u],g[u]);
h[u]=max(mx1+mx2+2,h[u]);
}
int pre[maxn],suf[maxn];
int pr[maxn],sf[maxn];
void dfs2(int u,int fa){
int len=f[u].size();
vector<int>q;
q.push_back(0);
for(int i=0;i<len+5;i++) pre[i]=suf[i]=pr[i]=sf[i]=-inf;
for(int i=0;i<len;i++){
int x=f[u][i];
if(x!=fa) q.push_back(x);
}
len=q.size()-1;
for(int i=1;i<=len;i++){
int x=q[i];
t[x]=max(t[x],t[u]);
pre[i]=max(pre[i-1],g[x]);
pr[i]=max(pr[i-1],h[x]);
}
for(int i=len;i>=1;i--){
int x=q[i];
suf[i]=max(suf[i+1],g[x]);
sf[i]=max(sf[i+1],h[x]);
}
for(int i=1;i<=len;i++){
int x=q[i];
p[x]=max(p[x],p[u]+1);
t[x]=max(p[u],t[x]);
}
for(int i=2;i<=len;i++){
int x=q[i];
t[x]=max(p[u]+1+pre[i-1],t[x]);
t[x]=max(pr[i-1],t[x]);
p[x]=max(pre[i-1]+2,p[x]);
}
for(int i=1;i<len;i++){
int x=q[i];
t[x]=max(p[u]+1+suf[i+1],t[x]);
t[x]=max(sf[i+1],t[x]);
p[x]=max(suf[i+1]+2,p[x]);
}
for(int i=2;i<len;i++){
int x=q[i];
t[x]=max(t[x],pre[i-1]+suf[i+1]+2);
}
int mx1=-inf,mx2=-inf;
for(int i=1;i<=len;i++){
int x=q[i];
t[x]=max(mx1+mx2+2,t[x]);
if(g[x]>mx1){
mx2=mx1;
mx1=g[x];
}else if(g[x]>mx2){
mx2=g[x];
}
}
mx1=mx2=-inf;
for(int i=len;i>=1;i--){
int x=q[i];
t[x]=max(mx1+mx2+2,t[x]);
if(g[x]>mx1){
mx2=mx1;
mx1=g[x];
}else if(g[x]>mx2){
mx2=g[x];
}
}
for(int i=1;i<=len;i++){
int x=q[i];
int dis=max(max(t[x],h[x]),(t[x]+1)/2+(h[x]+1)/2+1);
if(dis<ans){
ans=dis;
ans1=pii(x,u);
}
}
for(int i=0;i<(int)f[u].size();i++){
int x=f[u][i];
if(x==fa) continue;
dfs2(x,u);
}
}
int pe[maxn],vis[maxn];
queue<int>q;
int bfs(int fa){
int ret=fa;
memset(vis,0,sizeof(vis));
memset(pe,0,sizeof(pe));
q.push(fa);
vis[fa]=1;
while(!q.empty()){
int u=q.front();
q.pop();
ret=u;
int len=f[u].size();
for(int i=0;i<len;i++){
if(!vis[f[u][i]]){
q.push(f[u][i]);
pe[f[u][i]]=u;
vis[f[u][i]]=1;
}
}
}
return ret;
}
int fq[maxn],tot;
void dfs(int u,int s){
if(u==0) return;
fq[++tot]=u;
dfs(pe[u],s);
}
int find(int x){
tot=0;
int s=bfs(x);
int t=bfs(s);
dfs(t,s);
return fq[(tot+1)/2];
}
void work(){
for(int i=1;i<=n;i++){
f[i].clear();
}
for(int i=1;i<n;i++){
int a=e[i].fi,b=e[i].se;
if(a==ans1.fi&&b==ans1.se) continue;
if(b==ans1.fi&&a==ans1.se) continue;
f[a].push_back(b);
f[b].push_back(a);
}
ans2.fi=find(ans1.fi);
ans2.se=find(ans1.se);
cout<<ans<<endl;
cout<<ans1.fi<<" "<<ans1.se<<endl;
cout<<ans2.fi<<" "<<ans2.se<<endl;
}
int main(){
ios::sync_with_stdio(false);
//freopen("in","r",stdin);
cin>>n;
for(int i=1,a,b;i<n;i++){
cin>>a>>b;
f[a].push_back(b);
f[b].push_back(a);
e[i]=pii(a,b);
}
dfs1(1,0);
dfs2(1,0);
work();
return 0;
}