Q:给定一个只包含正整数的非空数组。是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
注意:
每个数组中的元素不会超过 100
数组的大小不会超过 200
示例 1:
输入: [1, 5, 11, 5]
输出: true
解释: 数组可以分割成 [1, 5, 5] 和 [11].
示例 2:
输入: [1, 2, 3, 5]
输出: false
解释: 数组不能分割成两个元素和相等的子集.
A:01背包问题
1.引用:经典动态规划:0-1背包问题的变体
那么对于这个问题,我们可以先对集合求和,得出sum,把问题转化为背包问题:
给一个可装载重量为sum/2的背包和N个物品,每个物品的重量为nums[i]。现在让你装物品,是否存在一种装法,能够恰好将背包装满?
第一步要明确两点,「状态」和「选择」。
状态就是「背包的容量」和「可选择的物品」,选择就是「装进背包」或者「不装进背包」。
第二步要明确dp数组的定义。
按照背包问题的套路,可以给出如下定义:
dp[i][j] = x表示,对于前i个物品,当前背包的容量为j时,若x为true,则说明可以恰好将背包装满,若x为false,则说明不能恰好将背包装满。
比如说,如果dp[4][9] = true,其含义为:对于容量为 9 的背包,若只是用前 4 个物品,可以有一种方法把背包恰好装满。
或者说对于本题,含义是对于给定的集合中,若只对前 4 个数字进行选择,存在一个子集的和可以恰好凑出 9。
根据这个定义,我们想求的最终答案就是dp[N][sum/2],base case 就是dp[..][0] = true和dp[0][..] = false,因为背包没有空间的时候,就相当于装满了,而当没有物品可选择的时候,肯定没办法装满背包。
第三步,根据「选择」,思考状态转移的逻辑。
回想刚才的dp数组含义,可以根据「选择」对dp[i][j]得到以下状态转移:
如果不把nums[i]算入子集,或者说你不把这第i个物品装入背包,那么是否能够恰好装满背包,取决于上一个状态dp[i-1][j],继承之前的结果。
如果把nums[i]算入子集,或者说你把这第i个物品装入了背包,那么是否能够恰好装满背包,取决于状态dp[i - 1][j-nums[i-1]]。
首先,由于i是从 1 开始的,而数组索引是从 0 开始的,所以第i个物品的重量应该是nums[i-1],这一点不要搞混。
dp[i - 1][j-nums[i-1]]也很好理解:你如果装了第i个物品,就要看背包的剩余重量j - nums[i-1]限制下是否能够被恰好装满。
换句话说,如果j - nums[i-1]的重量可以被恰好装满,那么只要把第i个物品装进去,也可恰好装满j的重量;否则的话,重量j肯定是装不满的。

这里引用一下别人给的图片:
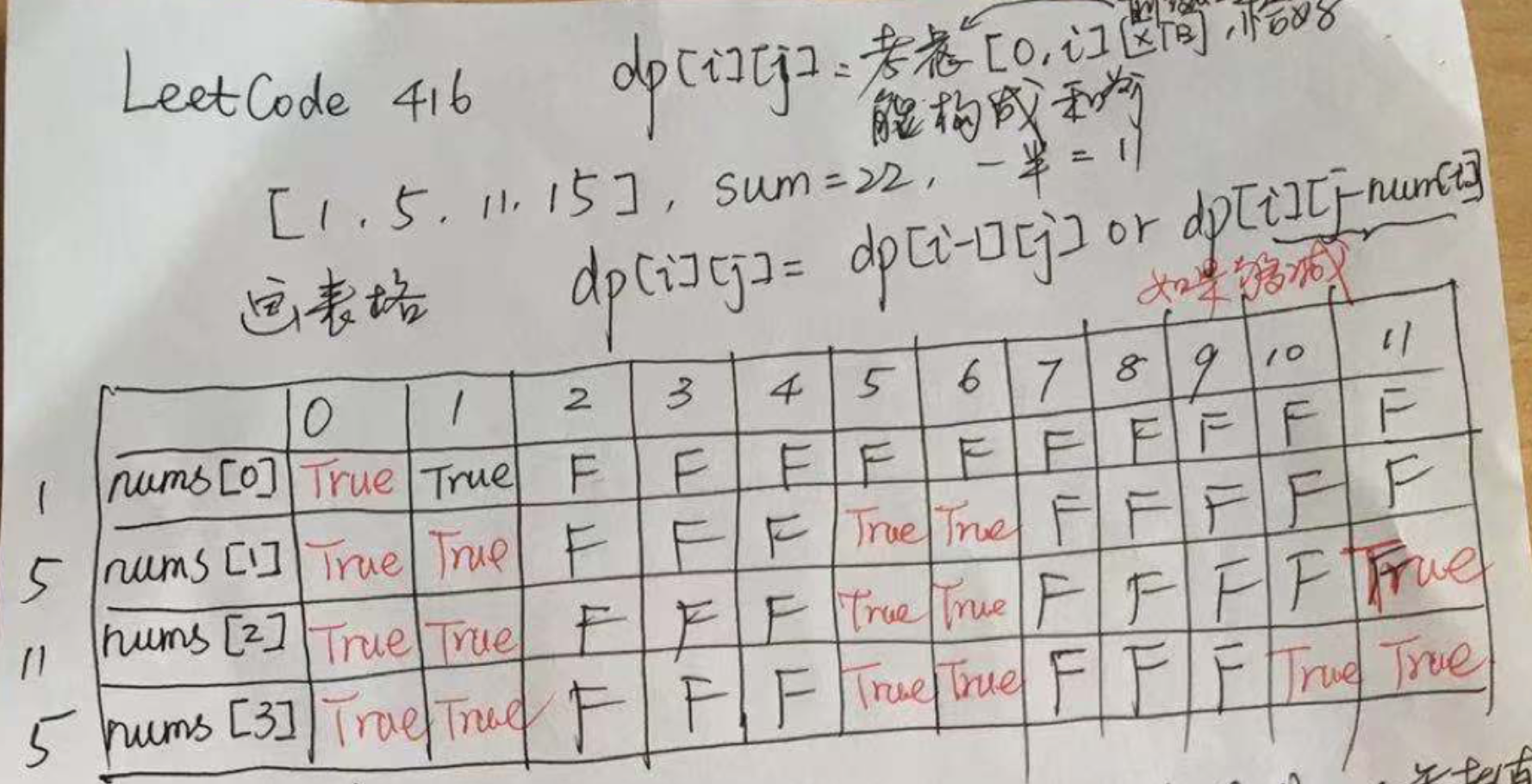
代码:
public boolean canPartition(int[] nums) {
if (nums.length <= 1)
return false;
int sum = 0;
for (int i : nums)
sum += i;
if (sum % 2 != 0)
return false;
sum /= 2;
int N = nums.length;
boolean[][] dp = new boolean[N + 1][sum + 1];
for (int i = 0; i <= N; i++) {
dp[i][0] = true;
}
for (int i = 1; i <= N; i++) {
for (int j = 1; j <= sum; j++) {
if (j - nums[i - 1] < 0) {
dp[i][j] = dp[i - 1][j];
} else {
dp[i][j] = dp[i - 1][j] || dp[i - 1][j - nums[i - 1]];
}
}
if(dp[i][sum])
return true;//剪枝
}
return dp[N][sum];
}
2.从后向前遍历法:
“状态数组”从二维降到一维,减少空间复杂度。在“填表格”的时候,当前行总是参考了它上面一行 “头顶上” 那个位置和“左上角”某个位置的值。因此,我们可以只开一个一维数组,从后向前依次填表即可。“从后向前” 写的过程中,一旦 nums[i] <= j 不满足,可以马上退出当前循环,因为后面的 j 的值肯定越来越小,没有必要继续做判断,直接进入外层循环的下一层。相当于也是一个剪枝,这一点是“从前向后”填表所不具备的。
这个还是可以联系上面的动态规划手写结果对照看:
public boolean canPartition(int[] nums) {
if (nums.length <= 1)
return false;
int sum = 0;
for (int i : nums)
sum += i;
if (sum % 2 != 0)
return false;
sum /= 2;
int N = nums.length;
boolean[] dp = new boolean[sum + 1];
dp[0] = true;
for (int i = 0; i < N; i++) {
for (int j = sum; nums[i] <= j; j--) {
if (dp[sum])
return true;//同样也是剪枝
dp[j] = dp[j] || dp[j - nums[i]];
}
}
return dp[sum];
}