LeetCode——最低成本联通所有城市

Q：

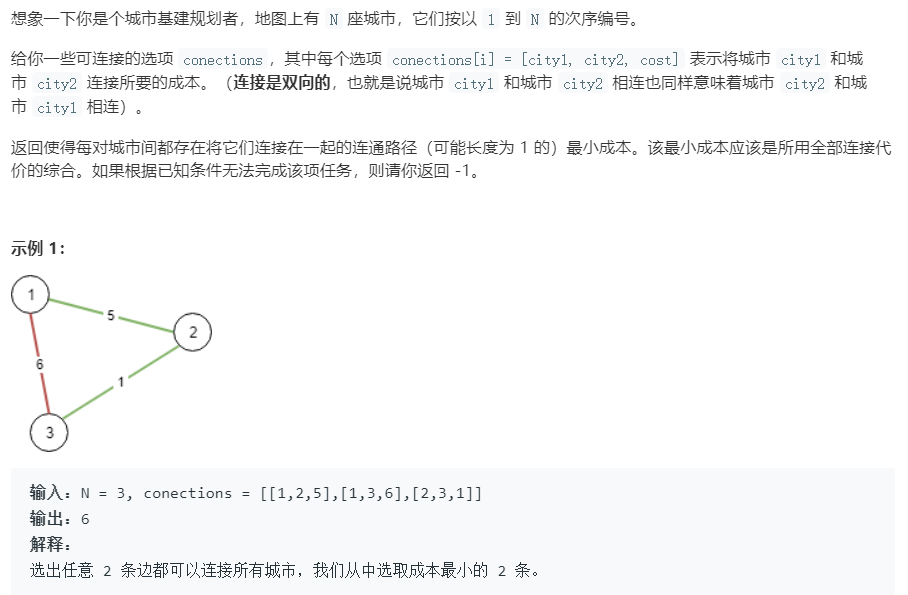
A：
典型最小生成树问题。
图的生成树是一棵含有其所有的顶点的无环联通子图，一幅加权图的最小生成树（ MST ） 是它的一颗权值（树中所有边的权值之和）最小的生成树。
根据题意，我们可以把 N 座城市看成 N 个顶点，连接两个城市的成本 cost 就是对应的权重，需要返回连接所有城市的最小成本。很显然，这是一个标准的最小生成树

注意，图中边的顶点是从1开始的，但我们一般从0开始，所以点在存储时常常要减一

kruskal 算法

既然我们需要求最小成本，那么可以肯定的是这个图没有环（如果有环的话无论如何都可以删掉一条边使得成本更小）。该算法就是基于这个特性：
按照边的权重顺序（从小到大）处理所有的边，将边加入到最小生成树中，加入的边不会与已经加入的边构成环，直到树中含有 N - 1 条边为止。这些边会由一片森林变成一个树，这个树就是图的最小生成树。

Union类：

class Union {
    int count;//树的个数
    int[] root;//每个点的根节点
    int[] size;//一棵树的节点数

    Union(int m) {
        root = new int[m];
        size = new int[m];
        for (int i = 0; i < m; i++) {
            root[i] = i;//初始点，每个点的根节点都是自己
            size[i] = 1;//每棵树只有1个节点
        }
        count = m;//总共有m棵树
    }

    public void unionF(int i, int j) {
        int x = find(i);//i的根节点
        int y = find(j);//j的根节点
        if (x != y) {
            if (size[x] > size[y]) {//x树更大，把y接上去
                root[y] = x;
                size[y] += size[x];
            } else {//y树更大，把x接上去
                root[x] = y;
                size[x] += size[y];
            }
            count--;
        }
    }

    public int find(int j) {
        while (root[j] != j) {
            //这句是为了压缩路径，不要的话可以跑的通，但效率变低
            root[j] = root[root[j]];
            j = root[j];
        }
        return j;
    }

    public int count() {
        return count;
    }

    public boolean connected(int i, int j) {
        int x = find(i);
        int y = find(j);
        return x == y;
    }
}

最小生成书代码：

    public int minimumCost(int N, int[][] connections) {
        if (N <= 1)
            return -1;
        if (connections.length < N - 1)//边数量小于点-1，不可能构成树
            return -1;
        Arrays.sort(connections, Comparator.comparingInt(t -> t[2]));//按权重排序
        Union u = new Union(N);
        int count = 1;
        int res = 0;
        for (int[] connect : connections) {
            if (u.connected(connect[0] - 1, connect[1] - 1))//两点曾经连接过，没必要再连
                continue;
            u.unionF(connect[0] - 1, connect[1] - 1);
            count++;
            res += connect[2];
            if (count == N)//所有点都连上了
                return res;
        }
        return -1;
    }

Prim算法

Prim 算法是依据顶点来生成的，它的每一步都会为一颗生长中的树添加一条边，一开始这棵树只有一个顶点，然后会添加 N - 1 条边，每次都是将下一条连接树中的顶点与不在树中的顶点且权重最小的边加入到树中。
算法流程：

1. 根据 connections 记录每个顶点到其他顶点的权重；
2. 设计一个flag，判断是否被读取过；；
3. 每次读取堆顶元素，如果曾经被读取过就不再读取，否则把其所有边加入堆；

代码：

      public int minimumCost(int N, int[][] connections) {
        if (N <= 1 || connections.length < N - 1)//边数量小于点-1，不可能构成树
            return -1;
        HashMap<Integer, ArrayList<int[]>> map = new HashMap<>();//顶和边
        for (int[] connect : connections) {
            if (map.containsKey(connect[0])) {
                ArrayList<int[]> array = map.get(connect[0]);
                int[] c = new int[]{connect[1], connect[2]};
                array.add(c);
                map.put(connect[0], array);
            } else {
                ArrayList<int[]> array = new ArrayList<>();
                int[] c = new int[]{connect[1], connect[2]};
                array.add(c);
                map.put(connect[0], array);
            }
            if (map.containsKey(connect[1])) {
                ArrayList<int[]> array = map.get(connect[1]);
                int[] c = new int[]{connect[0], connect[2]};
                array.add(c);
                map.put(connect[1], array);
            } else {
                ArrayList<int[]> array = new ArrayList<>();
                int[] c = new int[]{connect[0], connect[2]};
                array.add(c);
                map.put(connect[1], array);
            }
        }
        boolean[] flag = new boolean[N];
        Arrays.fill(flag, false);//判断是否读取过
        int start = connections[0][0];//起始点，可以随意取
        flag[start - 1] = true;
        int count = 1;
        PriorityQueue<int[]> pq = new PriorityQueue<>(Comparator.comparingInt(t -> t[1]));//设计堆
        pq.addAll(map.get(start));
        int res = 0;
        while (!pq.isEmpty()) {//若堆为空，还没把所有点读入，说明是无法连接的
            int[] c = pq.poll();
            if (flag[c[0] - 1])//该边另一个顶点已经读取过
                continue;
            else {
                pq.addAll(map.get(c[0]));
                flag[c[0] - 1] = true;
                count++;
                res += c[1];
            }
            if (count == N)//所有点都被读取过了
                return res;
        }
        return -1;
    }