LeetCode——覆盖？

Q：你有一块棋盘，棋盘上有一些格子已经坏掉了。你还有无穷块大小为1 * 2的多米诺骨牌，你想把这些骨牌不重叠地覆盖在完好的格子上，请找出你最多能在棋盘上放多少块骨牌？这些骨牌可以横着或者竖着放。

输入：n, m代表棋盘的大小；broken是一个b * 2的二维数组，其中每个元素代表棋盘上每一个坏掉的格子的位置。
输出：一个整数，代表最多能在棋盘上放的骨牌数。

示例 1：
输入：n = 2, m = 3, broken = [[1, 0], [1, 1]]
输出：2
解释：我们最多可以放两块骨牌：[[0, 0], [0, 1]]以及[[0, 2], [1, 2]]。（见下图）

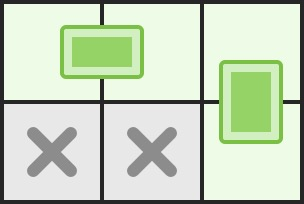
示例 2：
输入：n = 3, m = 3, broken = []
输出：4
解释：下图是其中一种可行的摆放方式

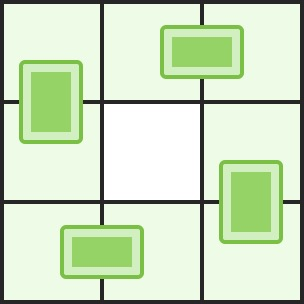
A：

DFS

第一反应就是DFS：
循环的过程是横向一行行逐格摆放，如到一行的末尾无法摆放则换行，如超过行数则计算摆放的最大个数

    private int max;
    private int curr;

    public int domino(int n, int m, int[][] broken) {
        max = 0;
        curr = 0;
        if (n == 0 || m == 0)
            return 0;
        boolean[][] check = new boolean[n][m];
        for (int i = 0; i < n; i++) {
            Arrays.fill(check[i], true);
        }
        for (int i = 0; i < broken.length; i++) {
            int x = broken[i][0];
            int y = broken[i][1];
            check[x][y] = false;
        }
        dfs(check, 0, 0);
        return max;
    }

    private void dfs(boolean[][] check, int x, int y) {
        if (x >= check.length) {
            max = Math.max(max, curr);
        } else if (y >= check[0].length) {
            dfs(check, x + 1, 0);
        } else if (!check[x][y]) {
            dfs(check, x, y + 1);
        } else {
            //横着放
            check[x][y] = false;
            boolean h = false;
            if (y + 1 < check[0].length && check[x][y + 1]) {
                h = true;
                check[x][y + 1] = false;
                curr++;
                dfs(check, x, y + 2);
                curr--;
                check[x][y + 1] = true;
            }

            //纵着放
            boolean v = false;
            if (x + 1 < check.length && check[x + 1][y]) {
                v = true;
                check[x + 1][y] = false;
                curr++;
                dfs(check, x, y + 1);
                curr--;
                check[x + 1][y] = true;
            }
            check[x][y] = true;
            if (!h && !v) {
                dfs(check, x, y + 2);
            }
        }
    }

匈牙利算法

代码：

    private boolean[] visit;// visit[v2]=true表示点v2访问过
    private int[] link;// link[v2]=v1表示当前与v2相连的点是v1
    // 其中v1属于点集V1，v2属于点集V2，数组下标从0开始

    private boolean[][] board;// 棋盘，false表示坏的
    private final int[] dir = new int[]{-1, 0, 1, 0, -1};

    public int domino(int n, int m, int[][] broken) {
        if (n == 0 || m == 0)
            return 0;

        // 初始化棋盘
        board = new boolean[n][m];
        for (int i = 0; i < n; i++) {
            Arrays.fill(board[i], true);
        }
        for (int i = 0; i < broken.length; i++) {
            board[broken[i][0]][broken[i][1]] = false;
        }
        visit = new boolean[n * m];
        link = new int[n * m];
        Arrays.fill(link, -1);
        return hungary(n, m);// 匈牙利算法计算最大骨牌数
    }

    private int hungary(int n, int m) {// 匈牙利算法，返回最大匹配数
        int curr = 0;
        // 遍历点集V1中的点
        for (int i = 0; i < n; i++) {
            for (int j = ((i & 1) == 0 ? 0 : 1); j < m; j += 2) {
                if (board[i][j]) {
                    Arrays.fill(visit, false);
                    if (find(n, m, i, j)) {
                        curr++;
                    }
                }
            }
        }
        return curr;// 返回最大匹配数
    }

    private boolean find(int n, int m, int x, int y) {
        for (int i = 0; i < dir.length - 1; i++) {
            // 四个相邻点
            int newx = x + dir[i];
            int newy = y + dir[i + 1];
            if (newx < 0 || newx >= n || newy < 0 || newy >= m) {
                continue;// 越界
            }
            int v2 = newx * m + newy;
            if (board[newx][newy] && !visit[v2]) {// 完好并且未访问过
                visit[v2] = true;
                if (link[v2] == -1 || find(n, m, link[v2] / m, link[v2] % m)) {
                    link[v2] = x * m + y;
                    return true;// 找到增广路径
                }
            }
        }
        return false;// 找不到增广路径
    }