Q:给定一个无序的整数数组,找到其中最长上升子序列的长度。
示例:
输入: [10,9,2,5,3,7,101,18]
输出: 4
解释: 最长的上升子序列是 [2,3,7,101],它的长度是 4。
说明:
可能会有多种最长上升子序列的组合,你只需要输出对应的长度即可。
你算法的时间复杂度应该为 O(n2) 。
进阶: 你能将算法的时间复杂度降低到 O(n log n) 吗?
A:找最长递增子序列长度:(这个比较简单,就找了一个现成的)
public int lengthOfLIS(int[] nums) {
int[] dp = new int[nums.length];
// dp 数组全都初始化为 1
Arrays.fill(dp, 1);
for (int i = 0; i < nums.length; i++) {
for (int j = 0; j < i; j++) {
if (nums[i] > nums[j])
dp[i] = Math.max(dp[i], dp[j] + 1);
}
}
int res = 0;
for (int i = 0; i < dp.length; i++) {
res = Math.max(res, dp[i]);
}
return res;
}
但这样的复杂度为O(N^2),可以对最长子序的数组进行维护
此处引用:一步一步推导出官方最优解法,详细图解
从一个例子开始。我们先考虑下面的数组的最长上升子序列:
[10, 9, 2, 5, 3, 7, 101, 4, 1]
用暴力法求解,可以得下图:
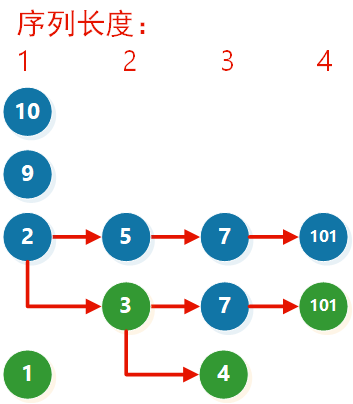
假如我们要在里面新增一个元素 X,希望找出插入 X 之后的最长子序列。
结论一指出,我们需要在当前允许插入的 最长 子序列之后添加元素。
于是,我们可以依次检查序列长度 = 1,2,3,4 的递增子序列,然后找出最长的,尾数 < X 的序列。
我们发现,对每一个序列长度 l,只需要检查图中的每一列的最小值(绿色的元素)是否 < X 即可。如果绿色的元素 < X,表明长度为 l 的递增子序列后可添加元素 X。
因此,我们有 结论二:我们只需要维护 长度为 l 的递增子序列的 最小结尾数字。
我们应该如何实现这样的算法呢?
最简单的实现方式,当插入新元素 X 时,我们从 1 逐个枚举现有递增子序列的长度,直到找到最大可添加元素 X 的长度。与此同时,维护每个长度 l 的最小尾数:
比如前述序列 [10, 9, 2, 5, 3, 7, 101, 4, 1],已构造 dp 数组[1, 3, 4, 101],要添加 “6”。
长度 l = 1 时,长度为 1 的递增子序列末尾的最小数字为 1,6 > 1,可以添加。
l = 2 时,6 > 3,可以添加。
l = 3 时,6 > 4,可以添加。
l = 4 时,6 < 101,不可添加。
因此,以 “6” 为结尾的递增子序列最长为 3 + 1 = 4。
另外,此时,长度为 4 的递增子序列的最小尾数变成了 “6”。因此修改 “101” -> “6”。数组变为 [1, 3, 4, 6]。
由于数组是有序的,当要添加数 “x” 时,可以用二分搜索找出数组中小于 x 的最大数字。
public int lengthOfLIS(int[] nums) {
int n = nums.length;
if (n <= 1)
return n;
ArrayList<Integer> array = new ArrayList<>();
array.add(nums[0]);
for (int i = 1; i < n; i++) {
int index = Binary(array, nums[i], 0, array.size());//二分法查找该替代的位置
if (index == array.size())
array.add(nums[i]);//如果比最大的还大,放到队尾
else {
array.set(index, nums[i]);//取代当前位置
}
}
return array.size();
}
private int Binary(ArrayList<Integer> array, int num, int start, int end) {
int left = start, right = end;
while (left < right) {
int mid = (left + right) / 2;
if (array.get(mid) == num) {
right = mid;
} else if (array.get(mid) > num) {
right = mid;
} else {
left = mid + 1;
}
}
return left;
}
Q:给定一个未排序的整数数组,找到最长递增子序列的个数。
示例 1:
输入: [1,3,5,4,7]
输出: 2
解释: 有两个最长递增子序列,分别是 [1, 3, 4, 7] 和[1, 3, 5, 7]。
示例 2:
输入: [2,2,2,2,2]
输出: 5
解释: 最长递增子序列的长度是1,并且存在5个子序列的长度为1,因此输出5。
注意: 给定的数组长度不超过 2000 并且结果一定是32位有符号整数。
A:
1.基于上一题的第一种解法,同样使用动态规划。找个数时,放一个count数组。
public int findNumberOfLIS(int[] nums) {
if (nums.length <= 1)
return nums.length;
int n = nums.length;
int[] length = new int[n];
int[] count = new int[n];
Arrays.fill(length, 1);
Arrays.fill(count, 1);
int maxLen = 0;
for (int i = 1; i < n; i++) {
for (int j = 0; j < i; j++) {
if (nums[i] > nums[j]) {
if (length[i] < length[j] + 1) {//更新最大长度子序列
length[i] = length[j] + 1;
count[i] = count[j];
} else if (length[i] == length[j] + 1) {//同样以i结尾的最大长度的子序列
count[i] += count[j];
}
}
}
maxLen = Math.max(maxLen, length[i]);
}
int res = 0;
for (int i = 0; i < n; i++) {
if (maxLen == length[i])
res += count[i];
}
return res;
}
2.基于上一题的第二种写法,用树状数组做
3.用CDQ分治
(这两个找时间再看吧)O(nlogn)的两种解法:树状数组和CDQ分治(新手慎入)