LeetCode——计算右侧小于当前元素的个数

Q：给定一个整数数组 nums，按要求返回一个新数组 counts。数组 counts 有该性质： counts[i] 的值是  nums[i] 右侧小于 nums[i] 的元素的数量。

示例:
输入: [5,2,6,1]
输出: [2,1,1,0]
解释:
5 的右侧有 2 个更小的元素 (2 和 1).
2 的右侧仅有 1 个更小的元素 (1).
6 的右侧有 1 个更小的元素 (1).
1 的右侧有 0 个更小的元素.

A：
1.分治法
考虑使用归并排序。
以题目所给的[5,2,6,1]为例，先把数组变成pairs，pairs里面存的是数值和初始所在的index，存初始index是为了往count里面存放数量时可以找到初始的这个值所对应的index。
使用分治，第一次归并的数组是[[5,0]|[2,1]].
初始化：

5比2大，先把[2,1]对应放到temp的位置上。

因为左侧没有读完，说明左侧没有读完的数比右侧的所有数都要大，所以5对应的count位置上要加上右侧所有的数字的总个数

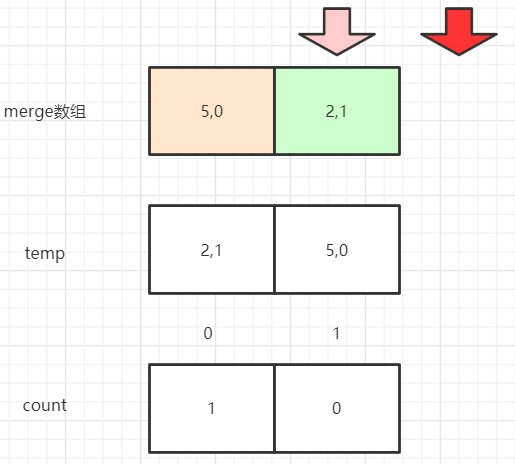
第二次归并的数组是[[6,2]|[1,3]]，类似上面，归并结果是[[1,3]，[6,2]]
当前count为[1,0,1,0]

第三次归并的数组是[[2,1],[5,0]|[1,3]，[6,2]]
初始化：

2比1大，1放入temp，j++

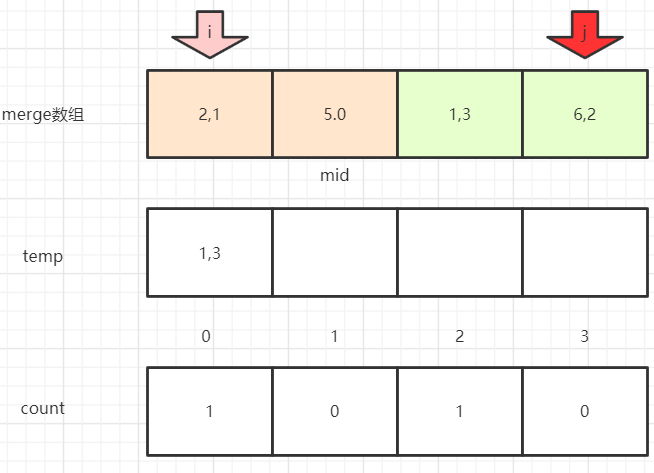
2比6小，说明2比6之前到mid的所有值都大（因为如果不比6左侧值都大不可能能让j移到6上去），所以把mid至6之间值的总个数加到2对应的count上，即j-mid-1 = 1
再把2放入temp，i++

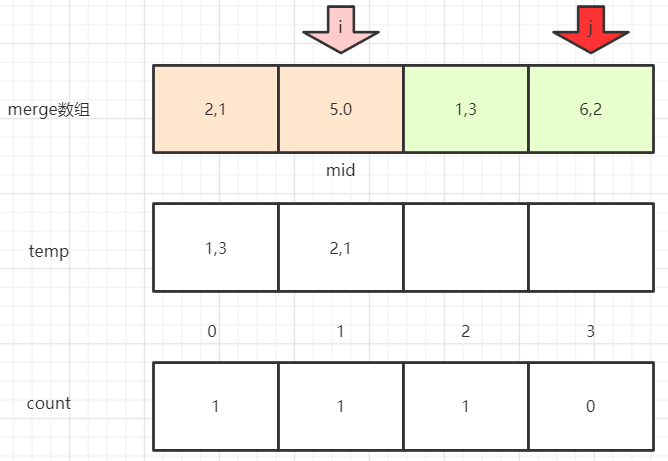
5比6小，说明5比6之前到mid的所有值都大，所以把mid至6之间值的总个数加到5对应的count上，即j-mid-1 = 1
再把5放入temp，i++

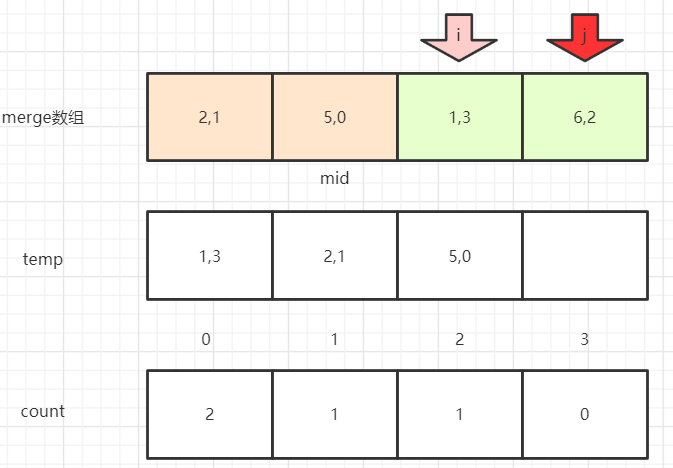
此时左侧所有数值都放入temp中，右侧还有6没放入。右侧当前已是最大，不可能右侧还有比其更小的值了，直接加入temp中

至此，已完成count的计算。

代码：

    private int[] count;

    public List<Integer> countSmaller(int[] nums) {
        List<Integer> result = new ArrayList<>();
        if (nums.length == 0)
            return result;
        int n = nums.length;
        Pair<Integer, Integer>[] pairs = new Pair[n];
        count = new int[n];
        for (int i = 0; i < n; i++) {
            pairs[i] = new Pair<>(nums[i], i);
        }
        merge_sort(pairs, 0, n - 1);
        for (int i = 0; i < n; i++)
            result.add(count[i]);
        return result;
    }

    private void merge_sort(Pair<Integer, Integer>[] pairs, int left, int right) {
        if (left >= right)
            return;
        int mid = (left + right) / 2;
        merge_sort(pairs, left, mid);
        merge_sort(pairs, mid + 1, right);
        merge(pairs, left, mid, right);
    }

    private void merge(Pair<Integer, Integer>[] pairs, int left, int mid, int right) {
        int i = left, j = mid + 1, k = left;
        Pair<Integer, Integer>[] temp = Arrays.copyOf(pairs, pairs.length);
        while (i <= mid && j <= right) {
            if (pairs[i].getKey() <= pairs[j].getKey()) {
                int index = pairs[i].getValue();
                count[index] += (j - mid - 1);//mid到j之间的所有数字都比i小
                temp[k] = pairs[i];
                i++;
                k++;
            } else {
                temp[k] = pairs[j];
                j++;
                k++;
            }
        }
        while (i <= mid) {//当前i比右侧数组的所有值都大
            int index = pairs[i].getValue();
            count[index] += right - mid;
            temp[k] = pairs[i];
            i++;
            k++;
        }
        while (j <= right) {
            temp[k] = pairs[j];
            j++;
            k++;
        }
        for (int m = left; m <= right; m++) {
            pairs[m] = temp[m];
        }
    }

2.使用二叉排序树
从后往前插入。
还是以[5,2,6,1]为例。
初始化：

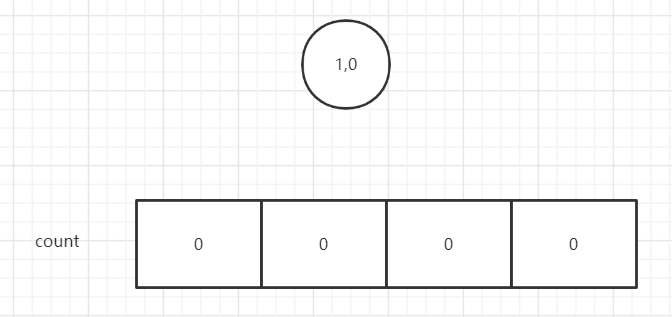
6比1大，插入右侧，存入的值在1的count上+1

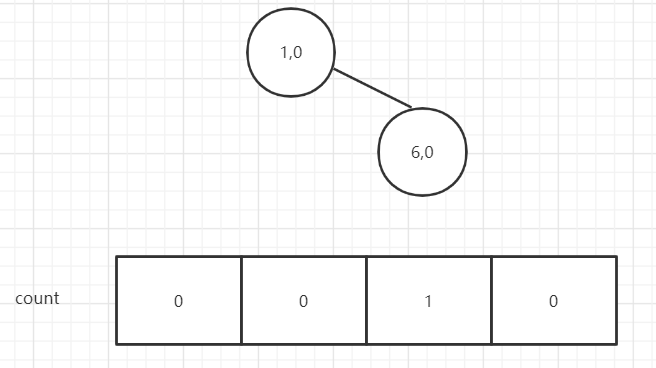
2比1大，存入值在1的count上+1；比6小，放入6左侧，6的count+1

5比1大，存入值在1的count上+1；比6小，放入6的左侧，6的count+1；比2大，存入值在2的count上+1

若是5前面还有一个7
7比1大，存入值在1的count上+1；比6大，存入值再存入6的count上+1

代码：

    class TreeNode {
        int val;
        int count;
        TreeNode left;
        TreeNode right;

        TreeNode(int val) {
            this.val = val;
            left = null;
            right = null;
            count = 0;
        }
    }

    public List<Integer> countSmaller(int[] nums) {
        List<Integer> result = new ArrayList<>();
        if (nums.length == 0)
            return result;
        int[] res = new int[nums.length];
        TreeNode root = null;
        for (int i = nums.length - 1; i >= 0; i--) {
            root = insert(root, new TreeNode(nums[i]), res, i);
        }
        for (int i : res) {
            result.add(i);
        }
        return result;
    }

    private TreeNode insert(TreeNode root, TreeNode node, int[] res, int i) {
        if (root == null) {
            root = node;
            return root;
        }
        if (node.val <= root.val) {
            root.count++;
            root.left = insert(root.left, node, res, i);
        } else {
            res[i] += root.count + 1;
            root.right = insert(root.right, node, res, i);
        }
        return root;
    }