Q:亚历克斯和李用几堆石子在做游戏。偶数堆石子排成一行,每堆都有正整数颗石子 piles[i] 。游戏以谁手中的石子最多来决出胜负。石子的总数是奇数,所以没有平局。亚历克斯和李轮流进行,亚历克斯先开始。 每回合,玩家从行的开始或结束处取走整堆石头。 这种情况一直持续到没有更多的石子堆为止,此时手中石子最多的玩家获胜。假设亚历克斯和李都发挥出最佳水平,当亚历克斯赢得比赛时返回 true ,当李赢得比赛时返回 false 。
示例:
输入:[5,3,4,5]
输出:true
解释:
亚历克斯先开始,只能拿前 5 颗或后 5 颗石子 。
假设他取了前 5 颗,这一行就变成了 [3,4,5] 。
如果李拿走前 3 颗,那么剩下的是 [4,5],亚历克斯拿走后 5 颗赢得 10 分。
如果李拿走后 5 颗,那么剩下的是 [3,4],亚历克斯拿走后 4 颗赢得 9 分。
这表明,取前 5 颗石子对亚历克斯来说是一个胜利的举动,所以我们返回 true 。
提示:
2 <= piles.length <= 500
piles.length 是偶数。
1 <= piles[i] <= 500
sum(piles) 是奇数。
A:
以下是对 dp 数组含义的解释:
dp[i][j].fir 表⽰,对于 piles[i...j] 这部分⽯头堆,先⼿能获得的最⾼分数。
dp[i][j].sec 表⽰,对于 piles[i...j] 这部分⽯头堆,后⼿能获得的最⾼分数。
举例理解⼀下,假设 piles = [3, 9, 1, 2],索引从 0 开始
dp[0][1].fir = 9 意味着:⾯对⽯头堆 [3, 9],先⼿最终能够获得 9 分。
dp[1][3].sec = 2 意味着:⾯对⽯头堆 [9, 1, 2],后⼿最终能够获得 2 分。
我们想求的答案是先⼿和后⼿最终分数之差,按照这个定义也就是 (dp[0][n-1].fir - dp[0][n-1].sec),即⾯对整个 piles,先⼿的最优得分和后⼿的最优得分之差。
写出状态转移⽅程:
dp[i][j].fir = max(piles[i] + dp[i+1][j].sec, piles[j] + dp[i][j-1].sec)
dp[i][j].fir = max( 选择最左边的⽯头堆 , 选择最右边的⽯头堆 )
# 解释:我作为先⼿,⾯对 piles[i...j] 时,有两种选择:
# 要么我选择最左边的那⼀堆⽯头,然后⾯对 piles[i+1...j]
# 但是此时轮到对⽅,相当于我变成了后⼿;
# 要么我选择最右边的那⼀堆⽯头,然后⾯对 piles[i...j-1]
# 但是此时轮到对⽅,相当于我变成了后⼿。
if 先⼿选择左边:
dp[i][j].sec = dp[i+1][j].fir
if 先⼿选择右边:
dp[i][j].sec = dp[i][j-1].fir
# 解释:我作为后⼿,要等先⼿先选择,有两种情况:
# 如果先⼿选择了最左边那堆,给我剩下了 piles[i+1...j]
# 此时轮到我,我变成了先⼿;
# 如果先⼿选择了最右边那堆,给我剩下了 piles[i...j-1]
# 此时轮到我,我变成了先⼿。
dp[i][j].fir = piles[i]
dp[i][j].sec = 0
其中 0 <= i == j < n
# 解释:i 和 j 相等就是说⾯前只有⼀堆⽯头 piles[i]
# 那么显然先⼿的得分为 piles[i]
# 后⼿没有⽯头拿了,得分为 0
如图,需要斜着遍历:
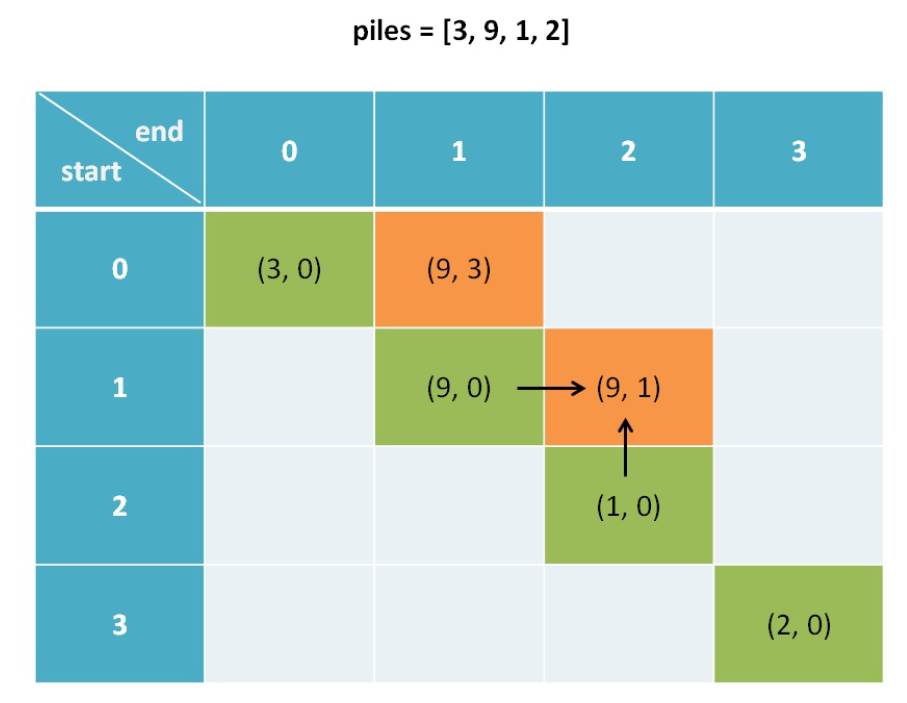
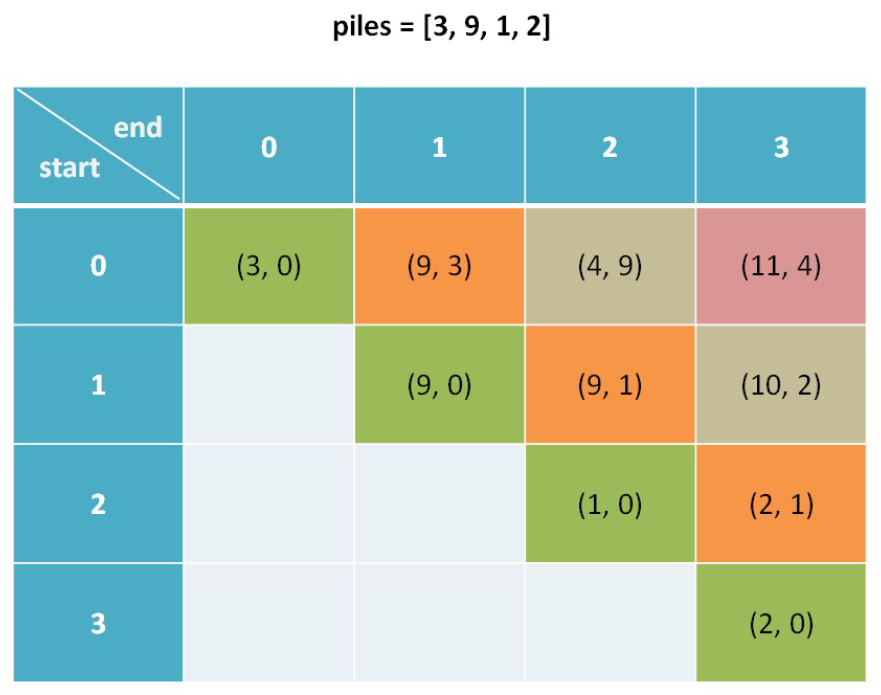
代码:
class Pair {
int first;
int second;
Pair(int first, int second) {
this.first = first;
this.second = second;
}
}
public boolean stoneGame(int[] piles) {
if (piles.length == 0)
return false;
int n = piles.length;
Pair[][] dp = new Pair[piles.length][piles.length];
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
dp[i][j] = new Pair(0, 0);
}
}
for (int i = 0; i < n; i++) {
//初始化
dp[i][i].first = piles[i];
dp[i][i].second = 0;
}
for (int i = n - 2; i >= 0; i--) {
for (int j = i + 1; j < n; j++) {
//当前堆是先拿左边,即为左边堆的后手
int left = piles[i] + dp[i + 1][j].second;
//当前堆是先拿右边,即为右边堆的后手
int right = piles[j] + dp[i][j - 1].second;
if (left >= right) {
dp[i][j].first = left;
dp[i][j].second = dp[i + 1][j].first;
} else {
dp[i][j].first = right;
dp[i][j].second = dp[i][j - 1].first;
}
}
}
return dp[0][n - 1].first > dp[0][n - 1].second;
}